啊哈C！源自《C语言参考手册》-整型数据溢出理解

先看实战案例，再看原理分析：
signed整型溢出是负数： 以short int 为例：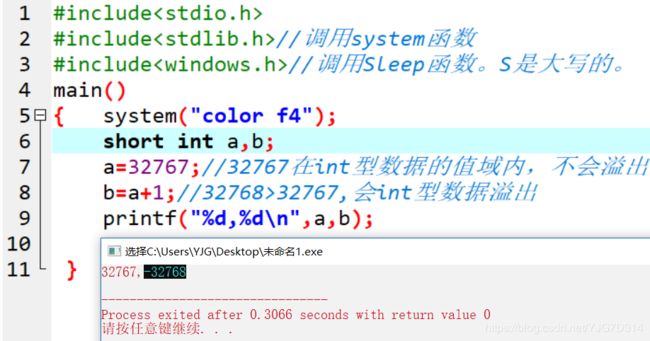
上面的代码会输出：32767，-32768。
千万别以为signed整型溢出就是负数，这个是不一定的。比如以int为例 signed整型溢出是正数：

上面的代码会输出：32767，32768。
signed整型溢出是正数： 以long int 为例

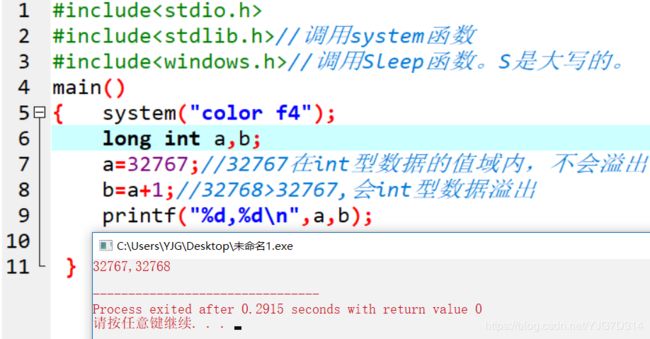
上面的代码会输出：32767，32768。
完整代码如下：

#include
#include//调用system函数 
#include//调用Sleep函数。S是大写的。 
main()
{	system("color f4");
    long int a,b;
    a=32767;//32767在int型数据的值域内，不会溢出 
    b=a+1;//32768>32767,会int型数据溢出 
	printf("%d,%d\n",a,b); 
	 
 } 

总结：对于signed整型的溢出，即int，short int，long int三种signed整型。对于大多数编译器来说，算得啥就是啥。可能为正，可能为负。以上结果可以说明。
思考：为什么溢出的数据是负的？原理是什么？原理是下面：
一个数在计算机中的二进制表示形式, 叫做这个数的机器数。机器数是带符号的，在计算机用一个数的最高位（最左边）存放符号, 即符号位。正数为0, 负数为1.这是-32768的理论依据。取值范围也要看有符号和无符号的，有符号将最高位看成符号位，有1和0，1正0负；无符号位将最高位看成数值位，不再讨论正负了。
32768的二进制：1000000000000000。最左边为1，符号位的符号是负的，故32768是负数，即-32768。
比如，十进制中的数 +3 ，计算机字长为8位，转换成二进制就是00000011。如果是 -3 ，就是 10000011 。
那么，这里的 00000011 和 10000011 就是机器数。
记住以下关键词：补码，反码。
值得注意的地方：下面划红线，圈起来的地方，即像-32768 short类型的值，严格标准的C程序是不能用short来表示-32768 的，但是使用二进制整数反码表现形式的计算机支持用short类型表示**-32768**。这也解释了上述案例为什么只有short整型溢出会是**-32768** ，就是使用二进制整数反码表现形式的计算机支持用short类型表示**-32768**。
还有就是补码的技术。它的编码方法如图中所述：
01.字的最高位（也就是最左端）是符号位。如果符号位是1，这个数就是负数，否则，这个数就是正数。 **这句话很重要，这句话是 ** -32768 的重要理论依据。请结合下面画红色箭头的图来正确理解。
02.何为补码技术？好高大上啊！
数值的表示方法——原码、反码和补码
原码：最高位为符号位，其余各位为数值本身的绝对值
反码： 正数：反码与原码相同 。负数：符号位为1，其余位对原码取反 反之，符号位为1，就是负数。
补码： 正数：原码、反码、补码相同 。负数：最高位为1，其余位为原码取反，再对整个数加1。
强调一下：数值的表示方法的意思是：一个数值，有上述原码，反码，补码3种方法。+7，-7，+0，-0。 图解如下：
-32768也可以用原码，反码，补码来表示。 下面开始介绍。

32767	32768
0111111111111111	1000000000000000

通过观察，我们发现，32768的二进制整数位的最高位（最左边）符号位是1，根据补码技术的方法，这个数是负数，即**-32768**。这就是**-32768的正确来历**！
反码技术来解释-32768：

32767	32768
0111111111111111	1000000000000000

根据反码的技术方法（还记得前面的反码概念吗？）
为什么要用到反码，补码？
现在我们知道了计算机可以有三种编码方式表示一个数. 对于正数因为三种编码方式的结果都相同:

[+1] = [00000001]原 = [00000001]反 = [00000001]补

所以不需要过多解释. 但是对于负数:

[-1] = [10000001]原 = [11111110]反 = [11111111]补

可见原码, 反码和补码是完全不同的. 既然原码才是被人脑直接识别并用于计算表示方式, 为何还会有反码和补码呢?
为了解决原码做减法的问题, 出现了反码:

计算十进制的表达式: 1-1=0

1 - 1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原= [0000 0001]反 + [1111 1110]反 = [1111 1111]反 = [1000 0000]原 = -0

发现用反码计算减法, 结果的真值部分是正确的. 而唯一的问题其实就出现在"0"这个特殊的数值上. 虽然人们理解上+0和-0是一样的, 但是0带符号是没有任何意义的. 而且会有[0000 0000]原和[1000 0000]原两个编码表示0。于是补码的出现, 解决了0的符号以及两个编码的问题:

1-1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原 = [0000 0001]补 + [1111 1111]补 = [0000 0000]补=[0000 0000]原

这样0用[0000 0000]表示, 而以前出现问题的-0则不存在了.而且可以用[1000 0000]表示-128:

(-1) + (-127) = [1000 0001]原 + [1111 1111]原 = [1111 1111]补 + [1000 0001]补 = [1000 0000]补

-1-127的结果应该是-128, 在用补码运算的结果中, [1000 0000]补 就是-128. 但是注意因为实际上是使用以前的-0的补码来表示-128, 所以-128并没有原码和反码表示.(对-128的补码表示[1000 0000]补算出来的原码是[0000 0000]原, 这是不正确的)

使用补码, 不仅仅修复了0的符号以及存在两个编码的问题, 而且还能够多表示一个最低数. 这就是为什么8位二进制, 使用原码或反码表示的范围为[-127, +127], 而使用补码表示的范围为[-128, 127].

因为机器使用补码, 所以对于编程中常用到的32位int类型, 可以表示范围是: [-231, 231-1] 因为第一位表示的是符号位.而使用补码表示时又可以多保存一个最小值.

以下为知识补丁：

原理分析：
1.分类
根据占用内存字节数的不同，整型变量又分为４类：
（1）基本整型（类型关键字为int）。也叫signed整型，有符号基本整型。
（2）短整型（类型关键字为short [int]）。也叫signed整型，有符号短整型。
（3）长整型（类型关键字为long [int]）。也叫signed整型，有符号长整型。
（4）无符号整型。也叫unsigned整型。
无符号型又分为无符号基本整型（unsigned [int]）、无符号短整型（unsigned short）和无符号长整型（unsigned long）三种，只能用来存储无符号整数。
2.占用内存字节数与值域
上述各类型整型变量占用的内存字节数，随系统而异。在16位操作系统中，一般用２字节表示一个int型变量，且long型（４字节）≥int型（２字节）≥short型（２字节）。
显然，不同类型的整型变量，其值域不同。如下表所示：

int的值域是【-32767，32767】，区间对称。因为-32768不在这个值域里，所以会溢出。为什么会有-32768上面已经详解了，现不再赘述。还记得溢出的定义吗？看下面解析：
3.整型变量数据溢出的概念
定义：数据超出规定的长度（值域）。对于整型溢出，分为无符号整型溢出和有符号整型溢出。 上面已经介绍过。
苏小红老师解释：如果我们定义了一个变量，然后又给变量赋了一个值，如果我们给这个变量赋的值，超出了这个变量的值域，这个时候结果会怎么样呢？发生数值溢出。图解如下：

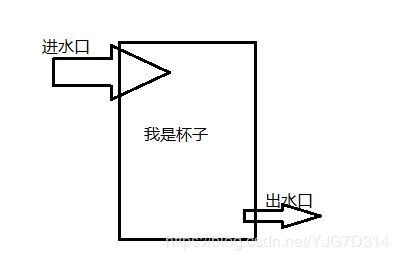
就像杯子装水，水满则溢。不同变量类型的存储空间相当于10毫升，20毫升，30毫升的杯子，依此类推。以10毫升为例，如果加入15毫升，就会发生水（数据）溢出，溢出（损失，丢失）5毫升的水（即数据）。那么溢出的数该如何表示？还记得前面的三种数据表示方法吗？一般用补码。
以int型变量数据溢出为例，首先它的值域是：-32767~32767（左边是负号）。如果超出了int型变量数据的值域，就会发生int型变量数据溢出，数据溢出的结果可能为正，可能为负，因编译器而异。
反思：整型溢出显然是一个错误的程序。我们不希望程序报错。所以，为了防止这个错误发生，我们应充分考虑各种数据的取值范围，使用合适的数据类型，减少失误。
**总结：**通过以上两种技术：反码，补码，都能解释整型溢出问题。一种问题，两种方法，均能实现。
目前浅析到此。2018-12-27.