图像处理代码编写三:基于C++的高斯滤波程序实现
认识高斯滤波
高斯滤波也叫高斯模糊,是一种线性平滑滤波器,高斯滤波适用于去除高斯噪声,即服从正态分布的噪声,在很多图像预处理的时候经常会用到高斯滤波来消除噪声。结合前篇均值滤波的博文,高斯滤波其实就是将滤波模板换成了高斯模板。在图像处理中,高斯滤波一般有两种实现方式,一是用离散化窗口滑窗卷积,另一种通过傅里叶变换。最常见的就是第一种滑窗实现,只有当离散化的窗口非常大,用滑窗计算量非常大(即使用可分离滤波器的实现)的情况下,可能会考虑基于傅里叶变化的实现方法。本次我们只讨论离散化窗口卷积。
高斯滤波原理
高斯滤波也是使用模板与图像进行卷积,与全部为一的均值滤波模板不同的地方在于高斯模板是从中心开始越远离中心值越小,相比均值滤波更能更能保持图像的细节。
二维高斯分布函数
二维高斯分布函数如下:
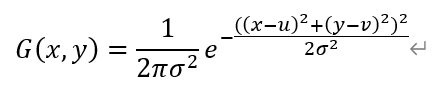
(x,y)为掩码内任意一点的坐标,(u,v)是掩码中心坐标,σ是其标准差。σ代表着数据的离散程度,如果σ较小,那么生成的模板的中心系数较大,而周围的系数较小,这样对图像的平滑效果就不是很明显;反之,如果σ较大,则生成的模板的各个系数相差就不是很大,相对来说对图像的平滑效果比较明显。我们计算的时候为了减少计算量把这一项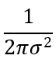
省略掉,因为它是常数,最后要进行归一化,不计算也没关系。
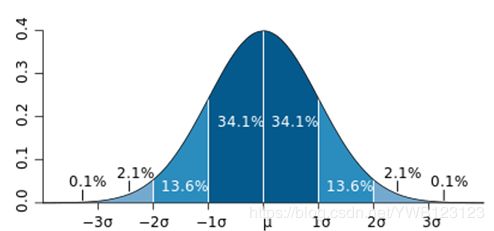
上图是一维高斯函数的函数图,可以很容易的联想到二维的情况。由该函数计算出来的模板需要进行归一化,也就是将计算出来的每个系数的值再除以所有系数的和,归一化的好处是能够保证之后卷积得出的新像素值再0到255的范围内。
代码实现
#include 分离高斯函数实现高斯滤波
由于高斯函数的可分离性,我们还可以用一种计算量相对小的方法实现高斯滤波。首先将图像在水平(竖直)方向与一维高斯函数进行卷积;然后将卷积后的结果在竖直(水平)方向使用相同的一维高斯函数得到的模板进行卷积运算。
假设水平方向的mask1的尺寸为1×W1,竖直方向的mask2的尺寸为H2×1,输入图片src的尺寸为H×W,第一种方法计算量大概为:(H×W)×(H2×W1);
第二种方法的计算量大概为:
(H×W)×(H2+W1)。
代码实现
//用分离高斯函数实现高斯滤波
void separateGaussianFilter(const Mat& src, Mat& dst, int ksize, double sigma)
{
dst = Mat::zeros(src.size(), src.type());
//获取一维高斯滤波模板
Mat mask;
mask.create(1, ksize, CV_64F);
int center = (ksize - 1) / 2;
double sum = 0.0;
for (int i = 0; i < ksize; i++)
{
mask.at<double>(0, i) = exp(-(pow(i - center, 2)) / (2 * sigma*sigma));
sum += mask.at<double>(0, i);
}
mask = mask / sum;
//边界填充
int boder = (ksize - 1) / 2;
Mat newsrc;
copyMakeBorder(src, newsrc, 0, 0, boder, boder, BORDER_DEFAULT);//边界复制
//高斯滤波--水平方向
for (int i = 0; i < src.rows; i++)
{
for (int j = boder; j < src.cols + boder; j++)
{
double sum[3] = { 0 };
for (int r = -boder; r <= boder; r++)
{
if (src.channels() == 1)
{
sum[0] += newsrc.at<uchar>(i, j + r) * mask.at<double>(0, r + boder); //行不变列变
}
else if (src.channels() == 3)
{
sum[0] += newsrc.at<Vec3b>(i, j + r)[0] * mask.at<double>(0, r + boder);
sum[1] += newsrc.at<Vec3b>(i, j + r)[1] * mask.at<double>(0, r + boder);
sum[2] += newsrc.at<Vec3b>(i, j + r)[2] * mask.at<double>(0, r + boder);
}
}
for (int k = 0; k < src.channels(); k++)
{
if (sum[k] < 0)
sum[k] = 0;
else if (sum[k] > 255)
sum[k] = 255;
}
if (src.channels() == 1)
{
dst.at<uchar>(i, j - boder) = static_cast<uchar>(sum[0]);
}
else if (src.channels() == 3)
{
Vec3b rgb = { static_cast<uchar>(sum[0]), static_cast<uchar>(sum[1]), static_cast<uchar>(sum[2]) };
dst.at<Vec3b>(i, j - boder) = rgb;
}
}
}
//高斯滤波--垂直方向
//对水平方向处理后的dst边界填充
copyMakeBorder(dst, newsrc, boder, boder, 0, 0, BORDER_DEFAULT);//边界复制
for (int i = boder; i < src.rows + boder; i++)
{
for (int j = 0; j < src.cols; j++)
{
double sum[3] = { 0 };
for (int r = -boder; r <= boder; r++)
{
if (src.channels() == 1)
{
sum[0] = sum[0] + newsrc.at<uchar>(i + r, j) * mask.at<double>(0, r + boder);
}
else if (src.channels() == 3)
{
Vec3b rgb = newsrc.at<Vec3b>(i + r, j);
sum[0] = sum[0] + rgb[0] * mask.at<double>(0, r + boder);
sum[1] = sum[1] + rgb[1] * mask.at<double>(0, r + boder);
sum[2] = sum[2] + rgb[2] * mask.at<double>(0, r + boder);
}
}
for (int k = 0; k < src.channels(); k++)
{
if (sum[k] < 0)
sum[k] = 0;
else if (sum[k] > 255)
sum[k] = 255;
}
if (src.channels() == 1)
{
dst.at<uchar>(i - boder, j) = static_cast<uchar>(sum[0]);
}
else if (src.channels() == 3)
{
Vec3b rgb = { static_cast<uchar>(sum[0]), static_cast<uchar>(sum[1]), static_cast<uchar>(sum[2]) };
dst.at<Vec3b>(i - boder, j) = rgb;
}
}
}
}
结果算起来确实比第一种方法快不少。
效果图
参考文献

