【Qt】实现波浪动画效果

所谓的波浪动画效果，就是多个正弦波形组合的效果。

先看看效果：

既然要画正弦波形，那就得先来了解正弦波，要绘制正弦波，其函数必须要了解。下面重拾高中知识，再一次再进正弦函数

正弦函数的物理意义：

y = A * sin(ωx + φ) ，A叫做振幅，T = 2π/ω叫做周期，f = 1/T = ω/2π叫做频率，ω叫角频率，ωx + φ叫做相位，x = 0时的相位φ称为初相

 

由y = sin(x)的图像通过变换得到y = A * sin(ωx + φ)

1.振幅变换：

y = Asin(x)的图像可以看座把正弦曲线上的所有点的纵坐标伸长（A>1）或缩短（0<ω<1）原来的A倍得到的（横坐标不变），它的值域为[-A, A],最大值是A，最小值是-A。如A<0可先作y = -Asin(x)的图像，再以x轴为对称轴翻折。A称为振幅

2.周期变换：

y = sin(ωx)的图像，可看作把正弦曲线上的所有点的横坐标缩短（ω>1）或伸长（0<ω<1）到原来的1/ω倍（纵坐标不变）。若ω<0则可用诱导公式将符号“提出”再作图。ω决定了函数的周期

3.相位变换：

y = sin(x + φ)的图像，可以看作把正弦曲线上所有点向左（当φ>0时）或向右（当φ<0时）平行移动|φ|个单位长度而得到。（即左加右减）

一般的，函数y = A * sin(ωx + φ)的图像可以看作是用下面的方法得到的：

（1）先把y = sin(x)的图像上所有的点向左（φ>0）或向右（φ<0）平行移动|φ|个单位

（2）再把所得的点的横坐标缩短（ω>1）或伸长（0<ω<1）到原来的1/ω倍（纵坐标不变）

（3）再把所得的各点的纵坐标伸长（A>1）或缩短（0

 

了解了正弦函数的物理意义之后，就可以开始结合我们的场景进行画图

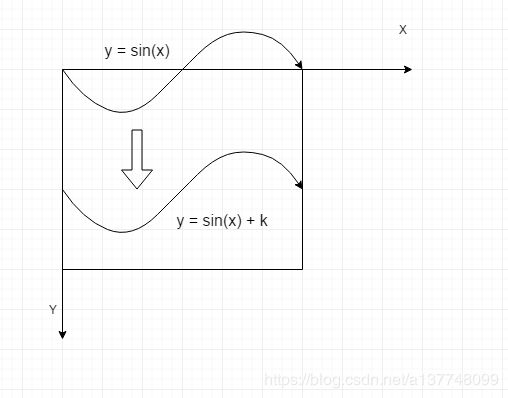
首先qt画图的坐标系是x向右，y向下为正方向，假设屏幕就显示一个周期，即2π/ω = 屏幕的宽，振幅A可自行定义选择，通过改变相位φ的值实现左右移动的动画效果，这样就能以像素为单位的一个正弦图，函数为y = A * sin(ωx + φ)，x和y的单位为像素，把整个图像向下移动就得到y = A * sin(ωx + φ) + k；

有了函数图像就可以画图了

以一个周期为例，以屏幕的宽的像素为x值，遍历从0->屏幕的宽，就可以得到对应的y的坐标，把所得的y的坐标画线连起来，就得到对应的图形。动画效果就是不断按顺序改变相位φ就能得到连续变化的正弦图。

这就是整个绘制正弦图的原理。

下面看代码：

void WavePlotAnimal::initUi()
{
    m_pTimer = new QTimer(this);
    m_pTimer->setInterval(160);
    connect(m_pTimer, &QTimer::timeout, this, &WavePlotAnimal::onTimeout);

    QPushButton *startBtn = new QPushButton(this);
    connect(startBtn, &QPushButton::clicked, this, [=](){
        m_pTimer->start();
    });
}

void WavePlotAnimal::paintEvent(QPaintEvent *event)
{
    QPainter painter(this);
    painter.setRenderHints(QPainter::Antialiasing | QPainter::SmoothPixmapTransform);
    painter.setBrush(QColor("#87CEFA"));
    painter.setPen(Qt::NoPen);
    painter.drawRect(this->rect());
//    painter.drawPixmap(QRect(0, 0, this->width(), 768), m_bg);
//    painter.drawPixmap(QRect(width()/2 - 111, 270, 222, 164), m_logoBg);
//    painter.drawPixmap(QRect(width()/2 - 119, 447, 237, 81), m_nameBg);

    //起始点坐标和结束点坐标
    int startX = 0;
//    int startY = 300;
    int endX = width() - 0;
    int endY = height() - 0;

    //第一条波浪路径集合
    QPainterPath waterPath1;
    //第二条波浪路径集合
    QPainterPath waterPath2;
    //第三条波浪路径集合
    QPainterPath waterPath3;
    QPainterPath waterPath4;


    //移动到左上角起始点
    waterPath1.moveTo(startX, endY);
    waterPath2.moveTo(startX, endY);
    waterPath3.moveTo(startX, endY);
    waterPath4.moveTo(startX, endY);

    //正弦曲线公式 y = A * qSin(ωx + φ) + k
    //A表示振幅,可以理解为水波的高度
    //k表示y轴偏移,控制在垂直方向显示的位置
    //φ控制x轴偏移，通过定时器控制实现动画效果
    //w表示周期,可以理解为水波的密度,值越大密度越大(浪越密集 ^_^),取值 密度*M_PI/宽度
    double w = Density*M_PI/this->width();

    offset += 0.6;
    for(int i = 0; i <= this->width(); i++){
        double y1 = (double)(50 * sin(-w * i + offset)) + 718;
        double y2 = (double)(60 * sin(-w * i + offset + 200*w)) + 688;
        double y3 = (double)(60 * sin(-w/2*i + offset + 400*w)) + 728;
        double y4 = (double)(60 * sin(-w * i + offset - 300*w)) + 708;
        waterPath1.lineTo(i, y1);
        waterPath2.lineTo(i, y2);
        waterPath3.lineTo(i, y3);
        waterPath4.lineTo(i, y4);
    }

    //形成闭合路径
    waterPath1.lineTo(endX, endY);
    waterPath2.lineTo(endX, endY);
    waterPath3.lineTo(endX, endY);
    waterPath4.lineTo(endX, endY);

    //颜色及透明度设置
    QColor waterColor1 = Qt::white;
    waterColor1.setAlpha(255);
    QColor waterColor2 = QColor("#7cc4c9");
    waterColor2.setAlpha(85);
    QColor waterColor3 = QColor("#1c8584");
    waterColor3.setAlpha(150);
    QColor waterColor4 = QColor("#d4fdd8");
    waterColor4.setAlpha(70);

    //绘制path
    painter.setBrush(waterColor2);
    painter.drawPath(waterPath2);

    painter.setBrush(waterColor3);
    painter.drawPath(waterPath3);

    painter.setBrush(waterColor4);
    painter.drawPath(waterPath4);

    painter.setBrush(waterColor1);
    painter.drawPath(waterPath1);

    QWidget::paintEvent(event);
}

void WavePlotAnimal::onTimeout()
{
    update();
}