对于OpenGL投影以及相机变换的一些理解
查了很多资料都有点想不明白投影到底干什么的,其实有时候不用想太多,以实际效果来做测试一下就明白了。
正交投影
首先我们图上先有一个立方体
float vertices[] = {
//第一面
-0.5f, -0.5f, -0.5f, 0.0f, 0.0f,
0.5f, -0.5f, -0.5f, 1.0f, 0.0f,
0.5f, 0.5f, -0.5f, 1.0f, 1.0f,
0.5f, 0.5f, -0.5f, 1.0f, 1.0f,
-0.5f, 0.5f, -0.5f, 0.0f, 1.0f,
-0.5f, -0.5f, -0.5f, 0.0f, 0.0f,
//第二面
-0.5f, -0.5f, 0.5f, 1.0f, 1.0f,
0.5f, -0.5f, 0.5f, 1.0f, 0.0f,
0.5f, 0.5f, 0.5f, 1.0f, 1.0f,
0.5f, 0.5f, 0.5f, 1.0f, 1.0f,
-0.5f, 0.5f, 0.5f, 0.0f, 1.0f,
-0.5f, -0.5f, 0.5f, 0.0f, 0.0f,
-0.5f, 0.5f, 0.5f, 1.0f, 0.0f,
-0.5f, 0.5f, -0.5f, 1.0f, 1.0f,
-0.5f, -0.5f, -0.5f, 0.0f, 1.0f,
-0.5f, -0.5f, -0.5f, 0.0f, 1.0f,
-0.5f, -0.5f, 0.5f, 0.0f, 0.0f,
-0.5f, 0.5f, 0.5f, 1.0f, 0.0f,
0.5f, 0.5f, 0.5f, 1.0f, 0.0f,
0.5f, 0.5f, -0.5f, 1.0f, 1.0f,
0.5f, -0.5f, -0.5f, 0.0f, 1.0f,
0.5f, -0.5f, -0.5f, 0.0f, 1.0f,
0.5f, -0.5f, 0.5f, 0.0f, 0.0f,
0.5f, 0.5f, 0.5f, 1.0f, 0.0f,
-0.5f, -0.5f, -0.5f, 0.0f, 1.0f,
0.5f, -0.5f, -0.5f, 1.0f, 1.0f,
0.5f, -0.5f, 0.5f, 1.0f, 0.0f,
0.5f, -0.5f, 0.5f, 1.0f, 0.0f,
-0.5f, -0.5f, 0.5f, 0.0f, 0.0f,
-0.5f, -0.5f, -0.5f, 0.0f, 1.0f,
-0.5f, 0.5f, -0.5f, 0.0f, 1.0f,
0.5f, 0.5f, -0.5f, 1.0f, 1.0f,
0.5f, 0.5f, 0.5f, 1.0f, 0.0f,
0.5f, 0.5f, 0.5f, 1.0f, 0.0f,
-0.5f, 0.5f, 0.5f, 0.0f, 0.0f,
-0.5f, 0.5f, -0.5f, 0.0f, 1.0f
};这个立方体十分简单,就是垂直于屏幕 z轴-0.5到0.5之间的一个立方体。后面两个坐标代表纹理的坐标。我们OpenGL使用的是右手坐标系
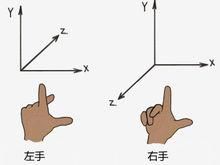
那么正常情况下我们会看到第二面,第二面的Z轴是离我们近的。然后我们使用正交投影的矩阵对坐标进行变换。
projection = glm::ortho(-1.0f, 1.0f, -ratio, ratio,0.1f, 10.0f);
我们先暂且不看前面4个参数,注意这里的投影矩阵是左手坐标系,那么我们可以理解为Z轴在0.1到10的范围内都可以显示。而转化为左手坐标系的OpenGL就代表在-0.1到-10的Z轴都是可见的。那么这样的话,我们就会看到第一个面,因为投影 的立方体是从物体中间传过去的。实际测试也是如此。
前面几个参数的作用是指定投影的立方体左右上下的范围,实际测试的效果就是,会根据传参的不同比例而对坐标进行缩放。比如这个立方体在手机上每一个面看起来都是个长方形,外面把ratio设置为手机屏幕宽和高的比,这样就会把y轴投影成和实际坐标一样的,变成一个正方形,而不是因为宽高比不同而现实的长度不一样了。例如:
将ratio制定为1.6,那么实际的效果就会变成 x坐标缩放一倍,y轴缩放1.6倍。
这种投影在3D环境下基本用的比较少,手机上可以用来对横竖屏进行适配。
透视投影
projection = glm::perspective(glm::radians(45.0f), ratio, 0.1f, 100.0f);;
同样看先看最后两个参数,这个和正交投影类似,超过该返回的z值范围同样不会显示在投影屏幕上。
第三个参数ratio也是一个比例,我们通常设置为横向和竖向的比例,这样投影出来的物体同样可以按照实际设置的坐标来控制大小,不会因为屏幕比例的问题而造成长宽数值一样大而显示不一样大。
第一个参数是一个视野参数的弧度值。
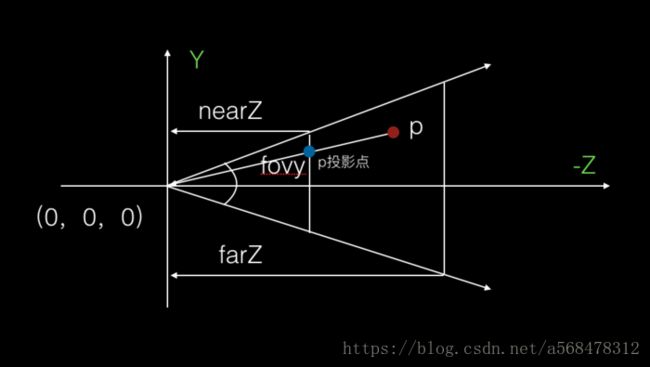
在生成的视椎体中,如果视野越大,视椎体的焦点也就越近,而投影在屏幕上的物体也就越小,该值在0-180度之间。
盗一张图来贴上,可以看得比较直观,摄像机越近投影物体越小,看到的物体就好像你的眼睛在哪个位置投影过来。

glm::lookAt
view = glm::lookAt(glm::vec3(0.0f, 0.0f, 3.0f),
glm::vec3(0.0f, 0.0f, 0.0f),
glm::vec3(0.0f, 1.0f, 0.0f)
);这个函数是用来调整相机位置的,第一个参数是代表相机在世界坐标系的位置,第二参数代表相机看的位置。这两个确定之后,想象一下相机还能怎么旋转,只能翻滚旋转吧。所以第三个参数就决定翻滚旋转的向量了,网上有的资料说是世界坐标系的向量,我也不知道到底对不对。我这里理解的是相机坐标系的向量,一般取(0.0f, 1.0f, 0.0f)的话我们就往上看,取(0.0,-1.0f.0.0f)的话整个图像就倒过来了,如果图像旋转90度的话很容易就想到是(1.0,0.0f.0.0f)了。