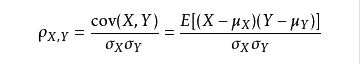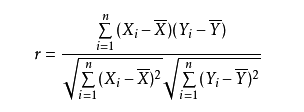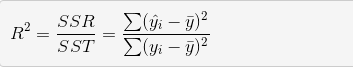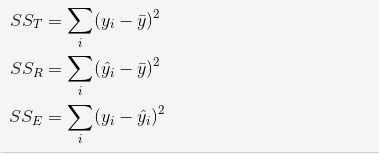9.回归中的相关度和决定系数
起步
训练集中可能有若干维度的特征。但有时并不是所有特征都是有用的,有的特征其实和结果并没有关系。因此需要一个能衡量自变量和因变量之间的相关度。
皮尔逊相关系数
皮尔逊相关系数( Pearson correlation coefficient),是用于度量两个变量 X 和 Y 之间的相关(线性相关),其值介于 -1 与 1 之间。
在说皮尔逊相关系数之前,要先理解协方差( Covariance ) ,协方差是一个反映两个随机变量相关程度的指标,如果一个变量跟随着另一个变量同时变大或者变小,那么这两个变量的协方差就是正值,反之相反,公式如下:
相关度越高,皮尔逊相关系数其值趋于 1 或 -1 (趋于1表示它们呈正相关, 趋于 -1 表示它们呈负相关);如果相关系数等于0,表明它们之间不存在线性相关关系。
对应的python实现
import math
import numpy as np
def computerCorrelation(x: list,y: list)-> float:
x_mean=np.mean(x)
y_mean=np.mean(y)
fenzi=0
var_x=0 #x的方差
var_y=0 #y的方差
for xi,yi in zip(x,y):
diff_x=xi-x_mean
diff_y=yi-y_mean
fenzi+=diff_x*diff_y
var_x+=diff_x**2
var_y+=diff_y**2
fenmu=math.sqrt(var_x*var_y)
return fenzi/fenmu
train_x=[1,3,8,7,9]
train_y=[10,12,24,21,34]
print(computerCorrelation(train_x,train_y))决定系数
决定系数即 R 平方值,反应因变量的全部变异能通过回归关系被自变量解释的比例。如R平方为0.8,则表示回归关系可以解释因变量80%的变异。换句话说,如果我们能控制自变量不变,则因变量的变异程度会减少 80%。 在简单线性回归中,绝对系数可以是 R^2 = r * r。而更通用的是:
from sklearn import linear_model
import numpy as np
def polyfit(x, y):
linear = linear_model.LinearRegression()
linear.fit(x, y)
y_hat = linear.predict(x)
y_mean = np.mean(y)
SSR = 0
SST = 0
for i in range(len(y)):
SSR += (y_hat[i] - y_mean) ** 2
SST += (y[i] - y_mean) ** 2
return SSR / SST
train_x=[1,3,8,7,9]
train_x_2d = [[x] for x in train_x] # 通用的方式,训练集至少是二维的
train_y=[10,12,24,21,34]
print(polyfit(train_x_2d,train_y))因为此为简单线性回归,所以其决定系数R^2的结果刚好是,相关系数的平方,有相应的结果可以看出。0.94^2![]() 0.88
0.88
修正决定系数
R 平方也有其局限性,随着自变量数目的增加,R 方是会增加的,这部分的定理是:
证明过程这里就省略了。http://www.hongweipeng.com/index.php/archives/1437/
调整后的R方表示为:
其中,n 表示样本大小,p 表示模型中解释变量的总数(个人理解为x的维度)(不包括常数)。