深入理解计算机系统第三版家庭作业答案-第二章
2.55-2.57答案:
show_bytes 源代码:
#include
typedef unsigned char* byte_pointer;
void show_bytes(byte_pointer ch, int len){
printf("show bytes:");
for (int i = 0; i < len; i++)
printf ("%.2x ", ch[i]);
printf("\n");
}
void show_short(short x)
{
show_bytes((byte_pointer) &x,sizeof(short ));
}
void show_long(long x)
{
show_bytes((byte_pointer) &x,sizeof(long ));
}
void show_double(double x)
{
show_bytes((byte_pointer) &x,sizeof(double ));
}
int main()
{
int x = 1;
short y = 32767;
long z = 32767;
double d = 3.14;
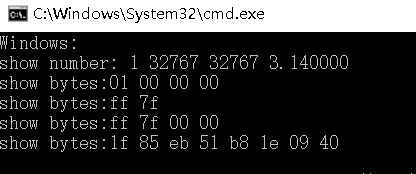
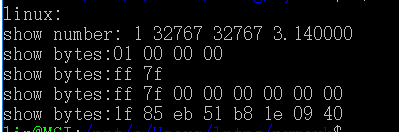
printf("linux:\nshow number: %d %d %ld %f\n",x,y,z,d);
show_bytes((byte_pointer) &x,sizeof(int ));
show_short(y);
show_long(z);
show_double(d);
return 0;
} 运行结果:
没有sum,windows10和linuxubuntu上运行结果都是小端字节序。
2.58
小端字节序下int x=1字节序为01 00 00 00
大端字节序下int x=1字节序为00 00 00 01
将其强制转换为char*类型返回第一个字节即可判断是小端还是大端
代码如下:
typedef unsigned char* byte_pointer;
int is_little_endian()
{
int x = 1;
return *((byte_pointer) &x);
}
注意数据类型都是转换为unsigned char* 而不是char*,这两个是会导致不同的输出结果。
2.59
int a = 0x89ABCDEF;
int b = 0x76543210;
printf("%02x\n",(a&0xFF)|(b&0xFFFFFF00));你也可以用不同的算法,我知道int是32位4字节故使用0xFFFFFF00,不知道下可以用~0xff来表示结果一样。
2.60
unsigned replace_byte(unsigned x,int i,unsigned char b)
{
i=i*8;
return (x&~(0xFF<2.61
代码如下:
#include
int YESORNO(int x)
{
return ( (!x) | (!(~x)) | (!(0xff&(~(x&0xff)))) | (!(x>>((sizeof(int)-1)<<3))) );
}
int main()
{
int x;
for(;;)
{
scanf("%x",&x);
printf("%d\n",YESORNO(x));
}
return 0;
} !x判断全为0情况
!(~x)判断全为1情况
(!(x>>((sizeof(int)-1)<<3)))判断最高字节位全为0情况,sizeof(int)32机子为4,x实际右移24位也就是将最高字节位移到最低字节位
(!(0xff&(~(x&0xff))))
先将x和0xff相与消除其他位的影响,取反后再相与,如果没有相与的话假设情况为0x000000ff那么取反后值为0x0xffffff00,多出来的几位ffffff将影响判断,故应该和0xff相与仅保留最低字节位,我们是判断最低字节为全1的情况。
运行结果:
2.62
int_shifts_are_arithmetic()
{
int x=-1;
return (x>>1)==-1;
}特殊情况-1字节序为0xffffffff 算术右移填充符号位1故值不变;逻辑右移填充0数值改变不为-1。
2.63
源代码:
#include
unsigned srl(unsigned x,int k)
{
unsigned xsra = (int) x >> k;
return (xsra&(~(-1<<(8*sizeof(int)-k))));
}
int sra(int x,int k)
{
int xsrl = (unsigned) x >> k;
int flag=(xsrl&(1<<(8*sizeof(int)-k-1)));
if(flag)//填充1
return (xsrl|(-1<<(8*sizeof(int)-k)));
else
return xsrl;
}
int main()
{
int x1,k;
for(;;)
{
scanf("%x %d",&x1,&k);
unsigned x2=unsigned(x1);
printf("逻辑右移:%02x>>%d -->%02x\n",x2,k,srl(x2,k));
printf("算术右移:%02x>>%d -->%02x\n",x1,k,sra(x1,k));
}
return 0;
} 运行结果:
2.64
x的32位bit中奇数位为1时候返回1,否则返回0源代码:
int any_odd_one(unsigned x)
{
return x & 0x55555555;
}2.65
x的32位bit包含奇数个1时候返回1否则返回0,源代码:
int odd_ones(unsigned x)
{
int count=0;
for(int i=0;i>i)&0x1)
count++;
return count;
} 看到最多包含12个算术运算觉得上面代码不符合,只能通过每位异或得到结果。
代码如下:
int any_ones(unsigned x){
x ^= (x >> 16);
x ^= (x >> 8);
x ^= (x >> 4);
x ^= (x >> 2);
x ^= (x >> 1);
return !(x&1);
} 2.66
说白了就是通过只保留最左边的那个1得到的数字,事例 0xff00-->0x8000,由上题思路和提示得到类似思路,将x最左边的1开始的后面的全部位变为1,如0x0100-->0x01ff,然后将其右移一位再和x异或来清除源代码:
int leftmost_one(unsigned x)
{
x |= (x >> 1);
x |= (x >> 2);
x |= (x >> 4);
x |= (x >> 8);
x |= (x >> 16);
return x^(x>>1);
}2.67
A问题出在1<<32
B只要排除大于32位情况就可以,既然不能移动32那么移动31次就好了,我们把1自己先左移一位变成2不就好了,改成2<<31即可这种方法返回结果是正确但是同样会警告忽略即可。
C加一个判断16位情况即可,代码:
int bad_int_size_is_32()
{
int before_msb = 0x2 << 15;
int set_msb = before_msb << 15;
int beyond_msb = set_msb<<1;
return before_msb && set_msb && !beyond_msb;
}以上代码在至少32位机器不会警告,但是16位机器会警告。
2.68
函数功能:输入n,输出比特位最右边为n个1的数字,源代码:
int lower_ones_mask(int n)
{
return (0x1<2.69
实现循环左移,代码:
int rotate_left(unsigned x,int n)
{
unsigned y=x>>(32-n);
x = x << n;
return (x|y);
}2.70
函数功能,输入x,n,判断x是否可以用n位比特数来表示,说白就是,前w-n+1位必须全是1或全是0,加的是n位比特数的符号位,源代码:
int fits_bits(int x,int n)
{
x=x>>(n-1);
return !x || !(~x);
}2.71
书上翻译太垃圾了,看了半天才知道要干嘛,首先有一个unsigned类型的数记为word 它由四字节组成,要求我们写个函数实现提取指定的单个字节出来,比如word为0x12345678,那么bytenum为0(0-3)时取出来0x78,然后,记得还没完,那位前任之所以被解雇就是因为没有然后,要将提取出来的数字转为有符号数,代码如下:
int xbyte(unsigned word ,int bytenum)
{
int y=word<<((3-bytenum)<<3);//将要提取的字节移到最高位
bytenum=sizeof(int)<<3;
return y>>bytenum;//用有符号数的算术右移来实现,无符号转有符号
}2.72
A:int转换为unsigned类型所以很小的时候比如int=-1会被转换为Umax,所以还是会判断成功
B 代码如下:
if(maxbytes >= sizeof(val) && maxbytes > 0)2.73
实现饱和加法,正溢出返回Tmax,负溢出返回Tmin,分别取x,y,sum的符号位填充到head_,接着判断head_x和head_y全为1而head_sum为0时候是负溢出,head_x和head_y全为0且head_sum全为1时候是正溢出,其余情况不溢出,故代码如下:
int saturating_add(int x,int y)
{
int Tmax=0x7fffffff;
int Tmin=0x80000000;
int sum=x+y;
int head_x=x>>31;
int head_y=y>>31;
int head_sum=sum>>31;
int flag_tmin=head_x&head_y&(~head_sum);
int flag_tmax=(~head_x)&(~head_y)&head_sum;
int flag_sum=~(falg_tmin|flag_tmax);
return sum&(flag_sum) | Tmax&(flag_tmax) | Tmin&(flag_tmin);
}2.74
代码如下:
int tsub_ok(int x,int y)
{
int sub=x-y;
if( (x>=0 && y<0 && sub=0 && sub>y) )
return 0;
else return 1;
} 2.75
要做这题必须走一遍乘法运算过程才好理解,假设w=4时候计算过程如图:
代码如下:
int add_out(unsigned x, unsigned y)
{
return x + y >= x;
}
unsigned unsigned_high_prod(unsigned x, unsigned y)
{
int w = sizeof(int)<<3;
unsigned high = 0;
unsigned sum = (y&0x1)?x:0;
for(int i=1; i>i) & 0x1 )
{
high += x>>(w-i);
if(!add_out(sum, x< 2.76
calloc函数代码:(可以自己在库函数找源码)
void *calloc(size_t nmemb ,size_t size)
{
unsigned long nsize=nmemb*size;
char *s;
if(nmemb==0 || size==0 || nsize>0xffff) return NULL;
else
{
s=malloc(nsize);
memset(s,0,(unsigned)nsize);
return s;
}
}2.77
A:x*17=x<<4+x;
B:x*(-7)=x*(1-8)=x-x<<3;
C:x*60=x*(64-4)=x<<6-x<<2;
D:x*(-112)=x*(16-126)=x<<4-x<<7;
2.78
正确的舍入方式应该是向零舍入,要求x/(2^k),知道x为正数时候就是向零取整,但是x为负数时候就是向下取整不合理,故使用下面表达式:
(x<0 ? x+(1<> k; 即可求得正确答案
2.79
求3*x/4;原式子可化为(x<<1+x)>>2,可以转换为x>>2+x>>1+低二位进位?1:0,比如x为0001bit位,那么要判断,01(x原来的低二位)和10(x左移一位后的低二位)是否有进位,如果有再加1;代码如下:
int mul3div4(int x) // 3*x/4
{
int cf=(((x<<1) & 0x3)+(x & 0x3)) >> 2;
return (x>>2)+(x>>1)+cf;
}2.80
以题目意思应该是求3/(4x),而不是3/4*x那样跟上题一样还有什么意思,思路差不多,当x为正数时候不考虑,当x为负数的时候,为了向上舍入,需要偏量4x-1,故代码如下:
x<0?(3+4*x-1)/(4*x):3/(4*x)2.81
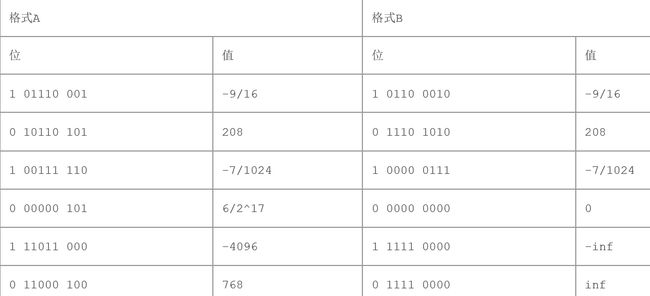
A:(~0)< B:((1< 2.82 A:但x为Tmin时候,-x也为Tmin故等式两边不想等 B:数学推到如下: C:同A,x为0x80000000时候会导致错误 D:无符号和有符号位级操作一样 E:先右移不存在溢出,然后再左移回来可知道只可能由于低二位的丢失造成数值变小故小于等于原值 2.83 A:题意:比如y=(01)那么Y=1,k=2,我们要求的是0.010101...值为多少,设为x,提示知道,x*2^k=Y+x-->x=Y/(2^k-1), B由A公式便可计算得到. 2.84 ux<=uy ^ (sy | sx) 六种情况: ux<=uy 为1时候,有三种 1.sx=0,sy=0,则返回1,因为都是正数 2.sx=0,sy=1,则返回0,因为y为负数,x为正数,必然是x>y; 3.sx=1,sy=1,则返回0,因为xy都为负数,绝对值小的反而大; ux<=uy为0时候,有三种: 1.sx=0,sy=0,则返回0 2.sx=1,sy=0,则返回1,因为x为正数,y为负数,必然x 3.sx=1,sy=1,则返回1,因为,xy都是负数,那么绝对值数值大的x反而小. 2.85 A:7.0 --> 111.0--> 1.11 -->E=2,M=1.11 ,f=0.11,V=7.0 e=2+2^k-1 B:最大奇整数:m=1.1111...1,E=n,f=0.111...1,V=M*2^n C:最小规格化数的倒数,最小规格化数是V=2^(-2^(k-1)+2),则1/V=2^(2^(k-1)-2),,则E=2^(k-1)-2,M=1,f=0.00; 参考课本p82 2.86 最小正非规格化数 0 | 0,,,0 | 0 | 0....01 非规格化E=1-bias=2-2^14,m=2^(-63),V=m*2^E 具体10进制自己按计算器可得 最小正规化数 0 | 0....1| 1 | 000..00 E=e-bias=2-2^14,m=1 最大规格化 0 | 111..0| 1 | 11...11 E=2^14-1 m=1.111..11 2.87 描述 hex M E V D -0 0x8000 0 -15 最小的>2的值 0x4001 1025/1024 1 1025*2^(-9) 2.00195315(手机计算器得到) 512 0x6000 1 9 最大非规格数 0x03ff 1023/1024 -14 1023*2^(-24) 0.000060975516 负无穷大 0xfc00 0x3BB0 0x7376 955/512 13 955*2^(4) 15280 2.88 2.89 A 错,因为Float表示证书低于double,Tmax float就表示不了,而double可以 B错误,因为x-y溢出时候,double不会溢出 C正确,都是正数不存在舍入问题,故可以用加法结合律 D乘法可能导致溢出问题,,比如,dx与dy相乘造成溢出,与dy和dz相乘造成的溢出不同,就会得到不同的结果. E错误,其中一个为0,另一个不为0时候 2.90 frac是低23位表示,exp是高9位表示,参考课本p82 图2-36 2.91 A11.0010 0100 0011 1111 0110 11 B根据提示对照公式x=Y/(2^k-1),得到k=3,Y=001 22/7=3+1/7 故表示为11.001001001... C第九位 2.92 2.93 2.94 2.95 偶数舍入,判断最后两位,01,00 10舍掉,11则加一位. 2.96 2.97 参考课本p86,关于强制转换原则,int转float不会溢出.17*y+15x=16(x+y)+y-x=(x+y)<<4+y-x;if (x<-149)
{
exp =0;
frac=0;
}
else if (x<-126)
{
exp =0;
frac=1<<(x+149);
}
else if (x<128)
{
exp =x+127;
frac=0;
}
else
{
exp =255;
frac=0;
}float_bits float_negate(float_bits f)
{
if( (f&0x7fffff) && ((f>>23) & 0xff) == 0xff )
return f;
else
return f^0x8000000000;
}float_bits float_absval(float_bits f)
{
if( (f&0x7fffff) && ((f>>23) & 0xff) == 0xff) )
return f;
else
return f&0x7fffffffff;
}float_bits float_twice(float_bits f)
{
unsigned sign=f>>31;
unsigned exp=(f>>23) & 0xff;
unsigned frac=f&0x7fffff;
if( exp == 0xff )
return f;
else if(exp==0)//非规格
return (sign<<31) | (frac<<1);
else if(exp<254)//规格
return (sign<<31) | ((exp+1)<<23) | (frac);
else//无穷大
return (sign<<31) | (0xff<<23);
}float_bits float_half(float_bits f)
{
unsigned sign=f>>31;
unsigned exp=(f>>23) & 0xff;
unsigned frac=f&0x7fffff;
if( exp == 0xff )
return f;
else if(exp==0)//非规格
return (sign<<31) | ((frac>>1)+(1 & (frac&3==3)));
else if(exp==1)//规格
return (sign<<31) | ((exp-1)<<23) | ( (frac>>1)&0x400000);
else
return (sign<<31) | ((exp-1)<<23) | frac;
}int float_f2i(float_bits f)
{
unsigned sign=f>>31;
unsigned exp=(f>>23) & 0xff;
unsigned frac=f&0x7fffff;
if( exp=0xff )
return 0x80000000;
else if(exp<127)//小于1的
return 0;
else if(exp>149)
frac = (0x800000^frac)<<(exp-149);
else
frac = (0x800000^frac)>>(149-exp);
return sign? -frac :frac;
}float_bits float_i2f(int i)
{
if(i==0) return 0;
unsigned x=i>0? i:-i;
unsigned exp=127;
unsigned sign =i&0x80000000;
unsigned frac=0;
int k;
unsigned mask;
for(k=0;k<32;k++)
if(x>>k==1) break;
exp+=k;
if(k<=23)
frac=x<<(23-k);
else{
frac = x>>(k-23);
mask=(0xffffffff>>(55-k));
if( (x&mask) == 1<<(k-24) )
frac += ( (x>>(k-23)) & 1);//为一半时候 进位取为要保留位最低位值;
else if( (x&mask) > 1<<(k-24))
frac++;
if(frac==(1<<24)) exp++;
}
return sign | (exp<<23) | (frac&0x7fffff);
}