【Ray Tracing】光线追踪基本概念与代码实现

I. 基本概念

具体的概念， 这里有一个很不错的 paper (https://raw.githubusercontent.com/quietshu/-paper-cg-RayTracing/master/RayTracing.pdf), 下载不下来的话，走这里。以下内容，引自这个paper。

光线追踪（Ray Tracing）算法是一种计算机三维图形渲染算法，其基本出发点就是追踪光线，模拟真实的光路和成像过程。相比于其他大部分渲染算法，光线追踪算法的优势是可以提供更为真实的光影效果，劣势是计算量巨大。

基于对自然界光路的研究，光线追踪采取逆向计算光路来还原真实颜色。模拟的过程中涵盖了光的反射、折射、吸收等特性（精确计算），并辅以其他重要渲染思想（模拟）。其中包含了重要方法，诸如冯氏光照模型（Phong Shading）、辐射度（Radiosity）、光子映射（Photon Mapping）、蒙特卡洛方法（Monto Carlo） 等等。

鉴于光线追踪算法对场景仿真程度之高，其被普遍认为是计算机图形学的核心内容，以及游戏设计、电影特效等相关领域的未来方向。近年来，由于硬件系统的迅速改良，基于分布式、GPU，甚至实时渲染的光线追踪算法也纷纷出现。

算法原理

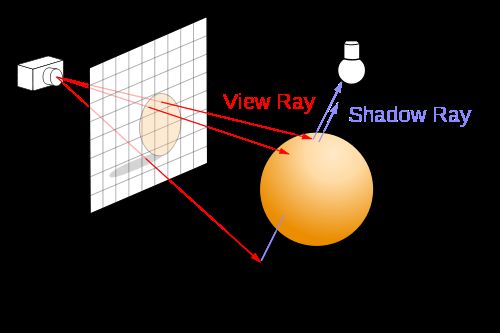
从视点出发向屏幕上每一个像素发出一条光线，追踪此光路并计算其逆向光线的方向，映射到对应的像素上。如下图，通过计算光路上颜色衰减和叠加，即可基本确定每一个像素的颜色。

基本框架

首先实现完整的空间向量类，包括相交检测、计算光线反射和折射。对反射和折射后的光线递归计算颜色再叠加起来即可算得原光线颜色。若光线未遇到任何物体则返回背景色。

在递归的过程中，光亮会不断衰减。因此可以限制迭代的深度或者光亮小于特定值时停止迭代。

将对应于每一个像素的光线颜色绘制到图片文件的相应坐标，最后输出绘制所得图像。光线颜色的基本递归算法伪代码如下

input : 光线的出发位置和方向向量
output : 反向光颜色

-----------------------------------------
function rayColor()

if no intersection with any object then
    return background color
else
    obj <- find nearest object from the ray;
    reflect ray <- calculate reflect ray with obj;
    refract ray <- calculate refract ray with obj;
    main color <- the radiance of obj;
    reflect color <- rayColor(reflect ray);
    refract color <- rayColor(refract ray);
    return mix(main color, reflect color, refract color);

基本元素

空间几何体

对于任意的几何体，都需要建立特定函数 f(x) f ( x ) 。自变量 x x 表示空间点的坐标，则

f(x)=⎧⎩⎨−1,0,1,点 x 在几何体外部点 x 在几何体表面上点 x 在几何体内部 f ( x ) = { − 1 , 点  x  在几何体外部 0 , 点  x  在几何体表面上 1 , 点  x  在几何体内部

空间光线

光线的参数方程

p=s+td p = s + t d

, 其中

• s s 是光线的起点坐标
• d d 是光线的方向向量
• t t 是前进距离标量，将光线试做射线，一般要求 t>0 t > 0

计算交点

复杂几何体都可以近似划分为基本几何体。作为基本框架，这里仅实现光线与球体和平面的相加。有以上几何体函数和光线方程联立可得交点的表达式为方程

f(p=s+td)=0 f ( p = s + t d ) = 0

. 求解出 t t 即可， t t 即为光出发点到与几何体交点走过的距离。

球体

球面方程为

|p−c|=r | p − c | = r

其中 p p 为空间中点的坐标. 依据球体的特征，可以建立函数 f(x)=sign(r−|p−c|) f ( x ) = sign ( r − | p − c | ) . 求光线与球面的交点，将 p=s+td p = s + t d 带入 f(t)=0 f ( t ) = 0 求解 t t 即可。结合实际的物理限制，若有交点，应取最近的交点，即 t t 取最小的正值。

平面

设平面法向量的坐标是 c c ，法向量方向为 N N ，则有 平面方程为

(p−c)⋅N=0 ( p − c ) ⋅ N = 0

, 带入光线方程即可求得交点坐标。

其他几何体

可以将复杂曲面划分为许多小平面（或三角形）的近似。因此将复杂问题划归为光线与空间内多边形求交点的问题。

首先求出光线与多边形所在平面的交点，将此交点的空间坐标向量与该平面的两个基向量相乘即可得到其对应于此平面的二维坐标。

判断平面上点与多边形的位置关系，可以使用经典的射线法。

反射光线

由反射定律，入射光线与反射光线、法线共面， 且两条光线关于法线对称。其中，法线向量是易于求得的，由几何关系容易得到

d′−d=2N d ′ − d = 2 N

, 其中 d' 是反射光线，故而可以直接求得。

折射光线

首先通过折射定律判断是否存在折射，如有则求出折射角。将入射光线、折射光线 和法线向量平移拼成三角形，由正弦定理和余弦定理即可求出折射光线。

Lambert 明暗模型

假设入射光线是 d d , 反射光线是 d′ d ′ , 入射点和光源的连线向量为 l l , 那么此处光亮可以定义为

k=cos<d′,l>=d′l∥d′∥∥l∥ k = cos < d ′ , l >= d ′ l ‖ d ′ ‖ ‖ l ‖

. 则此处反射颜色是原反射颜色乘以 k k 之后的值。

颜色

与传统的 255 色不同，在 Ray Tracing 中的颜色使用标准的全值域 RGB 模型。为了便于计算，将颜色表示为向量 (r,g,b) ( r , g , b ) , 其中 r,g,b r , g , b 均为 0 0 到 1 1 的实数。

光照颜色

RGB 值为 c1 c 1 的光线照射到RGB 值为 c2 c 2 的物体上，反射或折射后的颜色为 c1⊗c2 c 1 ⊗ c 2 , 其中 ⊗ ⊗ 为笛卡尔积。

(ToDo：两个三维向量的笛卡尔积应该是9个元素，怎么又变成的一个三维向量呢？)

叠加颜色

RGB 值为 c1 c 1 的光线和 RGB 值为 c2 c 2 的光线叠加后颜色为 c1⊕c2 c 1 ⊕ c 2 , ⊕ ⊕ 为笛卡尔和。叠加后大于 1 1 的 r,g,b r , g , b 值直接赋值为 1.

笛卡尔和又是什么东东？

颜色衰减

RGB 值为 c c 的光线照射在衰减度为 k k 的材质表面后，颜色表现为 kc k c .

物体属性

反射比例(reflect)

表示与物体相交后，有多少比例的光线产生了反射。

折射比例(refract)

表示与物体相交后，有多少比例的光线产生了折射。

Phong 光照模型

为了提供更为真实的渲染效果，Bui Tuong Phong 发明了 Phong 着色法。这种方法将漫反射(diffuse reflection) 和正反射(specular reflection) 叠加在一起，并给正反射加以高光，使得 光晕效果更加明显。

使用 Phong 着色法需要给物体添加许多额外的物理参数

• 漫反射亮度(diffuse) : 表示漫反射光的衰减比例
• 正反射亮度(specular)：表示正反射光的高光比例

光晕参数

光晕 在越接近正反射处表现的越明显，因此高光函数应选取一个机遇夹角余弦值的单调、且剧烈变化的函数。有多种模拟方法，上图选取了额外高光系数

s=cos50θ s = cos 50 ⁡ θ

, 此时物体的表现光由以下三个成分组成

obj.reflect * obj.specular * cos50θ * specularColor + obj.reflect * obj.diffuse * diffuseColor + obj.refract * refractColor obj.reflect * obj.specular *  cos 50 ⁡ θ  * specularColor + obj.reflect * obj.diffuse * diffuseColor + obj.refract * refractColor

阴影

阴影和高光一样，也是让渲染增强真实感不可缺少的元素。

计算方法

将入射光线和光源连线，若与物体相交则可判断此处有阴影。
若判断有阴影，则将 textobj.reflect,obj.refract t e x t o b j . r e f l e c t , o b j . r e f r a c t 两个参数乘上一个小于 1 1 的倍数，以产生变暗效果。这里取值 shadowRate=0.4 s h a d o w R a t e = 0.4

软阴影、抗锯齿 和 漫反射

上面产生的阴影，边缘太过尖锐，过渡不自然，没有现实中阴影的平滑。软阴影有两种常见渲染方法。

采样

任何物体都不等价于一个质点，光源亦如此。光源放大来看就是一个球体，因此阴影边缘的一个点可能被部分光源照到，那么它就是介于阴影和非阴影之间。有一种思路是计算被光照的比例，但是难以实现。目前被广泛应用的方法是“采样”。

我们随机在光源球体中取若干个点，并每次讲光源定于其中一点，计算阴影。这样计算若干次，每一次由于光源位置稍有不同，故阴影也不同。将这些结果叠加起来，根据概率知识，很容易发现当取点数量达到一定时，叠加起来的阴影越接近真实。

蒙特卡洛算法

蒙特卡洛算法是一大类随机算法的统称，也是另一种接近真实的渲染方法。在现实中不存在绝对平滑的物体，所以不存在正反射。利用这一点，可以在每一次计算反射光的时候随机偏离一个角度。如此随机很多次，再将颜色平均起来就得到这一点的颜色。蒙特卡洛算法既可以模拟计算漫反射，也可以计算软阴影。

给物体添加附属属性 粗糙度，代表这个随机角的范围。越粗糙的物体表面随机角越大。

软阴影和漫反射效果

镜头

纹理

通过照射点的三维坐标，可以还原出这个点对于此物体的坐标，基于此就能给物体加上纹理。例如对于平面有

x′=nx x ′ = n x

, 其中 n n 是平面的基向量， x x 是点的三维坐标， x′ x ′ 是点相对于平面的坐标。

改进后的光线追踪效果图

再对物体的各种参数进行微调，给平面添加纹理后得到的效果图如下

类似的，球面映射也可以通过极坐标（确定经纬度）来计算。

II. 代码实现

将第一部分的基本概念，用 C++ 实现 来构建初步的光线追踪框架，代码来自以下两位大神，我主要是整理验证了一遍

• 用JavaScript玩转计算机图形学(一)光线追踪入门:Milo Yip 大神的经典之作，带JS交互
• 一个系列，按 Milo Yip 的思路编排，使用 C++ 实现，带源码
  
  • 光线追踪(RayTracing)算法理论与实践(一)入门
  • 光线追踪(RayTracing)算法理论与实践(二)平面、材质、联合光线与物体求交
  • 光线追踪(RayTracing)算法理论与实践(三)光照

源代码下载：

• 光线追踪基本框架:C++源代码 ：
• 编译好的 GLFW 2.7.6 ，适用于 VS 2010。下载

好，下面来一步步实现

Step 0. 建立空间直角坐标系

这个坐标系怎么建都可以，但是建的好，可以方便想象和理解，简化运算。比如按照一定的规范，

• 原点选在核心焦点处，最好位于地面上
• 水平向右为 x x 轴正方向
• 水平向上为 y y 轴正方向
• 竖直向上为 z z 轴正方向

Step 1. 建立空间向量类

空间向量类 Vector3D, 既可以表示三维空间中的点，也可以表示三维空间中的向量。
实现参考上面链接。

Step 2. 实现光模型

要有光，便有了 Ray . 实现参考上面链接。

Step 3. 空间中放置模型

参考上面链接。

Step 4. 空间中放置摄像机

这个比较复杂，单开一篇，光线追踪中的相机模型

---

Ref

• 视觉技术的圣杯：光线追踪如何再现真实世界？ : 超级棒的综述报道，一文入坑