《大话数据结构》笔记——第6章 树（一）

6.1 开场白

略

6.2 树的定义

之前我们一直在谈的是一对一的线性结构，可现实中，还有很多一对多的情况需要处理，所以我们需要研究这种一对多的数据结构——“树”，考虑它的各种特性，来解决我们在编程中碰到的相关问题。

树（Tree）是 n（n>=0）个结点的有限集。

n=0 时称为空树。

在任意一棵非空树中：

（1）有且仅有一个特定的称为根（root）的结点。

（2）当 n>1 时，其余结点可以分为 m（m>0）个互不相交的有限集 T1，T2，T3……Tm，其中每个集合本身又是一棵树，并且称为根的子树（SubTree）。

如图 6-2-1 所示

树的定义其实就是我们在讲解栈时提到的递归的方法。也就是在树的定义之中还用到了树的概念，这是一种比较新的定义方法。图 6-2-2 的子树 T1 和子树 T2 就是根结点 A 的子树。当然，D、G、H、I 组成的树又是 B 为结点的子树，E、J 组成的树是 C 为结点的子树。

对于树的定义还需要强调两点：

1. n>0 时根结点是唯一的，不可能存在多个根结点，别和现实中的大树混在一起，现实中的树有很多根须，那是真实的树，数据结构中的树只能有一个根结点。

2. m>0 时，子树的个数没有限制，但它们一定是互不相交的。像图 6-2-3 中的两个结构就不符合树的定义。因为它们都有相交的子树。

   

6.2.1 结点分类

树的结点包含一个数据元素及若干个指向其子树的分支。结点拥有的子树数称为结点的度(Degree)。度为 0 的结点称为叶结点(Leaf)或终端结点；度不为 0 的结点称为非终端结点或分支结点。除根结点之外，分支结点也称为内部结点。树的度是树内各结点的度的最大值。如图 6-2-4 所示，因为这棵树结点的度的最大值是结点 D 的度，为 3，所以树的度也为 3。

6.2.2 结点间关系

结点的子树的根称为该结点的孩子(Child)。相应地，该结点称为孩子的双亲（Parent）。嗯，为什么不是父或母，叫双亲呢？呵呵，对于结点来说其父母同体，唯一的一个，所以只能把它称为双亲了。同一个双亲的孩子之间互称兄弟(Sibling)。结点的祖先是从根到该结点所经分支上的所有结点。所以对于 H 来说，D、B、A 都是它的祖先。反之，以某结点为跟的子树的任一结点都称为该结点的子孙。B 的子孙有 D、G、H、I，如图 6-2-5 所示。

6.2.3 树的其他相关概念

结点的层次(Level)从根开始定义起，根为第一层，根的孩子为第二层。若某结点在第 l 层，则其子树的根就在第 l+1层。其双亲在同一层的结点互为堂兄弟。显然图 6-2-6 中的 D、E、F 是堂兄弟，而 G、H、I、J 也是。树中结点的最大层次称为树的深度（Depth）或高度，当前树的深度为 4。

如果将树中结点的各子树看成从左到右是有次序的，不能互换的，则称该树为有序树，否则称为无序树。

森林（Forest）是 m(m>=0)棵互不相交的树的集合。对树中每个结点而言，其子树的集合即为森林。对于图 6-2-1 中的树而言，图 6-2-2 中的两棵子树其实就可以理解为森林。

对比线性表与树的结构，它们有很大的不同，如图 6-2-7 所示。

6.3 树的抽象数据类型

相对于线性结构，树的操作就完全不同了，这里我们给出一些基本和常用操作。

ADT 树（tree）
Data 
    树是由一个根结点和若干课子树构成。树中结点具有相同数据类型及层次关系。
Operation
    InitTree(*T)：构成空树 T。
    DestroyTree(*T)：销毁树 T。
    CreateTree(*T,Definition)：按 definition 中给出的树的定义来构造树。
    ClearTree(*T)：若树 T 存在，则将树 T 清为空树。
    TreeEmpty(T)：若 T 为空树，返回 true，否则返回 false。
    TreeDepth(T)：返回 T 的深度。
    Root(T)：返回 T 的根结点。
    Value(T,cur_e)：cur_e 是树T中一个结点，返回此结点的值。
    Assign(T,cur_e,value)：给树 T 的结点 cur_e 赋值为 value。
    Parent(T,cur_e)：若 cur_e 是树 T 的非根结点，则返回它的双亲，否则返回空。
    LeftChild(T,cur_e)：若 cur_e 是树 T 的非叶结点，否则返回它的最左孩子，否则返回空。
    RightSlibling(T,cur_e)：若 cur_e 有右兄弟，则返回它的右兄弟，否则返回空。
    InsertChild(*T,*p,i,c)：其中 p 指向树 T 的某个结点，i 为所指结点 p 的度加上 1，
        非空树 c 与 T 不相交，操作结果为插入 c 为树 T 中 p 指结点的第 i 棵子树。
    DeleteChild(*T,*p,i)：其中 p 指向树 T 的某个结点，i 为所指结点 p 的度，
        操作结果为删除 T 中 p 所指结点的第 i 棵子树。
endADT

6.4 树的存储结构

6.4.1 双亲表示法

树这种结构，除了根结点外，其余每个结点，它不一定有孩子，但是一定有且仅有一个双亲。

我们假设以一组连续空间存储树的结点，同时在每个结点中，附设一个指示器指示其双亲结点到链表中的位置。也就是说，每个结点除了知道自己是谁以外，还知道它的双亲在哪里。它的结点结构为表 6-4-1 所示。

其中 data 是数据域，存储结点的数据信息。而 parent 是指针域，存储该结点的双亲在数组中的下标。

以下是我们的双亲表示法的结点结构定义代码。

/* 树的双亲表示法结点结构定义 */
#define MAX_TREE_SIZE 100  //结点数组的大小 
typedef int TElemType; //树结点的数据类型，此处定位整型

/* 结点结构 */
typedef struct PTNode 
{
	TElemType data; //结点数据
	int parent; //双亲位置
}PTNode;
 
/* 树结构 */
typedef struct 
{
	PTNode nodes[MAX_TREE_SIZE]; //结点数组
	int r, n; //根的位置和结点数
}PTree;

有了这样的结构定义，我们就可以来实现双亲表示法了。由于根结点是没有双亲的，所以我们约定根结点的位置域设置为 -1，这也就意味着，我们所有的结点都存有它双亲的位置。如图 6-4-1 中的树结构和表 6-4-2 中的树双亲表示所示。

这样的存储结构，我们可以根据结点的 parent 指针很容易找到它的双亲结点，所用的时间复杂度为 O(1)，直到 parent 为 -1 时，表示找到了树结点的根。可如果我们要知道结点的孩子是什么，对不起，请遍历整个结构才行。

这真是麻烦，能不能改进一下呢？

当然可以。我们增加一个结点最左边孩子的域，不妨叫它长子域，这样就可以很容易得到结点的孩子。如果没有孩子的结点，这个长子域就设置为 -1，如表 6-4-3 所示。

对于有 0 个或 1 个孩子结点来说，这样的结构是解决了要找结点孩子的问题了。甚至是有 2 个孩子，知道了长子是谁，另一个当然就是次子了。

另外一个问题场景，我们很关注各兄弟之间的关系，双亲表示法无法体现这样的关系，那我们怎么办？嗯，可以增加一个右兄弟域来体现兄弟关系，也就是说，每一个结点如果它存在右兄弟，则记录下右兄弟的下标。同样的，如果右兄弟不存在，则赋值为 -1，如表 6-4-4 所示。

但如果结点的孩子很多，超过了 2 个。我们又关注结点的双亲、又关注结点的孩子、还关注结点的兄弟，而且对时间遍历要求还比较高，那么我们还可以把次结构扩展为有双亲域、长子域、再有右兄弟域。存储结构的设计是一个非常灵活的过程。一个存储结构设计得是否合理，取决于基于该存储结构的运算是否适合，是否方便，时间复杂度好不好等。注意也不是越多越好，有需要时再设计相应的结构。

6.4.2 孩子表示法

孩子表示法：把每个结点的孩子结点排列起来，以单链表作存储结构，则 n 个结点由 n 个孩子链表，如果是叶子结点则此单链表为空。然后 n 个头指针又组成一个线性表，采用顺序存储结构，存放进一个一维数组中，如图 6-4-4 所示。

为此，设计两种结点结构，一个是孩子链表的孩子结点，如表 6-4-7 所示。

其中 child 是数据域，用来存储某个结点在表头数组中的下标。next 是指针域，用来存储指向某结点的下一个孩子结点的指针。

另一个是表头数组的表头结点，如表 6-4-8 所示。

其中 data 是数据域，存储某结点的数据信息。firstchild 是头指针域，存储该结点的孩子链表的头指针。

以下是我们的孩子表示法的结构定义代码。

/* 树的孩子表示法结构定义 */
#define MAX_TREE_SIZE 100  
 
/* 孩子结点 */
typedef struct CTNNode 
{
	int child;
	struct CTNode *next;
}*ChildPtr;

/* 表头结构 */
typedef struct 
{
	TElemType data;
	ChildPtr firstchild;
}CTBox;

/* 树结构 */
typedef struct 
{
	CTBox nodes[MAX_TREE_SIZE]; //结点数组
	int r, n; //根的位置和结点数
}CTree;

这样的结构对于我们要查找某个结点的某个孩子，或者找某个结点的兄弟，只需要查找这个结点的孩子单链表即可。对于遍历整棵树也是很方便的，对头结点的数组循环即可。

但是，这也存在着问题，我如何知道某个结点的双亲是谁呢？比较麻烦，需要整棵树遍历才行，难道就不可以把双亲表示法和孩子表示法综合一下吗？当然是可以。如图 6-4-5 所示。

我们把这种方法称为双亲孩子表示法，应该算是孩子表示法的改进。

6.4.3 孩子兄弟表示法

刚才我们分别从双亲的角度和从孩子的角度研究树的存储结构，如果我们从树结点的兄弟的角度又会如何呢？当然，对于树这样的层级结构来说，只研究结点的兄弟是不行的，我们观察后发现，任意一棵树，它的结点的第一个孩子如果存在就是唯一的，它的右兄弟如果存在也是唯一的。因此，我们设置两个指针，分别指向该结点的第一个孩子和此结点的右兄弟。

结点结构如表 6-4-9 所示。

其中 data 是数据域，firstchild 为指针域，存储该结点的第一个孩子结点的存储地址，rightsib 是指针域，存储该结点的右兄弟结点的存储地址。

结构定义代码如下。

/* 树的孩子兄弟表示法结构定义 */
typedef struct CSNode
{
	TElemType data;
	struct CSNode *firstchild, *rightsib;
}CSNode,*CSTree;

对于图 6-4-1 的树来说，这种方法实现的示意图如图 6-4-6 所示。

这种表示法，给查找某个结点的某个孩子带来了方便，只需要通过 fistchild 找到此结点的长子，然后再通过长子结点的 rightsib 找到它的二弟，直到找到具体的孩子。当然，如果想找某个结点的双亲，这个表示法也是有缺陷的，那怎么办呢？

呵呵，对，如果真的有必要，完全可以再增加一个 parant 指针域来解决快速查找双亲的问题，这里就不再细谈了。

其实这个表示法的最大好处是它把一棵复杂的树变成了一棵二叉树。我们把图 6-4-6 变变形就成了图 6-4-7 这个样子。

6.5 二叉树的定义

二叉树：二叉树（Binary Tree）是 n（n ≥ 0）个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树的二叉树组成。

图 6-5-2 就是一棵二叉树。

6.5.1 二叉树特点

二叉树的特点有：

• 每个结点最多有两棵子树，所以二叉树中不存在度大于 2 的结点。注意不是只有两棵树，而是最多有。没有子树或者有一棵子树都是可以的。
• 左子树和右子树是有顺序的，次序不能任意颠倒。就像人是双手、双脚，但显然左手，左脚，右脚是不一样的，右手戴左手套、右脚穿左鞋都会极其别扭和难受。
• 即使树中某结点只有一棵子树，也要区分它是左子树还是右子树。图 6-5-3 中，树 1 和树 2 是同一棵树，但它们却是不同的二叉树。就好像你一不小心，摔伤了手，伤的是左手还是右手，对你的生活影响度是完全不同的。

二叉树具有五种基本状态：

1. 空二叉树
2. 只有一个根结点
3. 根节点只有左子树
4. 根结点只有右子树
5. 根节点既有左子树又有右子树

如果是有三个结点的树，有几种形态？如果是有三个结点的二叉树，考虑一下，又有几种形态？

若只从形态上考虑，三个结点的树只有两种情况，那就是图 6-5-4 中有两层的树 1 和有三层的后四种的任意一种，但对于二叉树来说，由于要区分左右，所以就演变成五种形态，树 2，树 3，树 4 和树 5 分别代表不同的二叉树。

6.5.2 特殊二叉树

斜树

顾名思义，斜树一定要是斜的，但是往哪斜还是有讲究。所有的结点都只有左子树的二叉树叫左斜树,所有结点都只有右子树的二叉树叫右斜树。这两者统称为斜树。图 6-5-4 中的树 2 就是左斜树，树 5 就是右斜树。斜树有很明显的特点，就是每一层都只有一个结点，结点的个数与二叉树的深度相同。

有人会想，这也能叫树呀，与我们的线性表结构不是一样吗。对的，其实线性表结构就可以理解为是树的一种极其特殊的表现形式。

满二叉树

在一棵二叉树中，如果所有分支结点都存在左子树和右子树。并且所有叶子都在同一层上，这样的二叉树称为满二叉树。

图 6-5-5 就是一棵满二叉树，从样子上看就感觉它很完美。

单是每个结点都存在左右子树，不能算是满二叉树，还必须要所有的叶子都在同一层上，这就做到了整棵树的平衡。因此，满二叉树的特点有：

1. 叶子只能出现在最下一层。出现在其他层就不可能达到平衡。
2. 非叶子结点的度一定是 2。否则就是"缺胳膊少腿"了。
3. 在同样深度的二叉树中，满二叉树的结点个数最多，叶子数最多。

完全二叉树

对一棵具有 n 个结点的二叉树按层序编号，如果编号为 i(1<=i<=n) 的结点与同样深度的满二叉树中编号为 i 的结点在二叉树中位置完全相同，则这课二叉树称为完全二叉树，如图 6-5-6 所示。

这是一种有些理解难度的特殊二叉树。

首先从字面上要区分，“完全” 和 “满” 的差异，满二叉树一定是一棵完全二叉树，但完全二叉树不一定是满的。

其次，完全二叉树的所有结点与同样深度的满二叉树，它们按层序编号相同的结点，是一一对应的。这里有个关键词是按层序编号，像图 6-5-7 中的树 1，因为 5 结点没有左子树，却有右子树，那就是使得按层序编号的第 10 个编号空挡了。同样道理，图 6-5-7 中的树 3 又是因为 5 编号下没有子树造成第 10 和 11 位置空挡。只有图 6-5-6 中的树，尽管它不是满二叉树，但是编号是连续的，所以它是完全二叉树。

从这里我也可以得出一些完全二叉树的特点：

1. 叶子结点只能出现在最下两层。
2. 最下层的叶子一定集中在左部连续位置。
3. 倒数二层，若有叶子结点，一定都在右部连续位置。
4. 如果结点度为1，则该结点只有左孩子，即不存在只有右子树的情况。
5. 同样结点数的二叉树，完全二叉树的深度最小。

从上面的例子。也给了我们一个判断某二叉树是否完全二叉树的办法，那就是根据树的示意图，给每个结点按照满二叉树的结构逐层顺序编号，如果编号出现空挡，就说明不是完全二叉树，否则就是。

6.6 二叉树的性质

6.6.1 二叉树性质 1

性质 1：在二叉树的第 i 层上至多有 2^(i-1) 个结点（i>=1）。

这个性质很好记忆，观察一下图 6-5-5。

• 第一层是根结点，只有一个，所以 2^(1-1)=2⁽⁰⁾=1。
• 第二层有两个，2^(2-1)=2⁽¹⁾=2。
• 第三层有四个，2^(3-1)=2⁽²⁾=4。
• 第四层有八个，2^(4-1)=2⁽³⁾=8。

通过数据归纳法的论证，可以很容易得出在二叉树的第 i 层上至多有 2^(i-1) 个结点 (i>=1) 的结论。

6.6.2 二叉树性质 2

性质 2：深度为 k 的二叉树至多有 2^(k)-1 个结点（k>=1）。

注意这里一定要看清楚，是 2^(k) 后再减去 1，而不是 2^(k-1)。以前很多同学不能完全理解，这样去记忆，就容易把性质 2 与性质 1 给弄混淆了。

深度为 k 意思就是有 k 层的二叉树，我们先来看看简单的。

• 如果有一层，至多 1=2⁽¹⁾-1 个结点。
• 如果有两层，至多 1+2=3=2⁽²⁾-1 个结点。
• 如果有三层，至多 1+2+4=7=2⁽³⁾-1 个结点。
• 如果有四层，至多 1+2+4+8=15=2⁽⁴⁾-1 个结点。

通过数据归纳法的论证，可以得出，如果有 k 层，此二叉树至多有 2^(k)-1 个结点。

6.6.3 二叉树性质3

性质 3：对任何一棵二叉树 T。如果其终端结点数为 n0，度为 2 的结点数为 n2，则 n0=n2+1。

终端结点数其实就是叶子结点数，而一棵二叉树，除了叶子结点外，剩下的就是度为 1 或 2 的结点数了，我们设 n1 为度是 1 的结点数。则树 T 结点总数 n=n0+n1+n2。

比如图 6-6-1 的例子，结点总数为 10，它是有 A、B、C、D 等度为 2 结点，F、G、H、I、J 等度为 0 的叶子结点和 E 这个度为 1 的结点组成。总和为 4+1+5=10。

我们换个角度，再数一数它的连接线数，由于根结点只有分支出去，没有分支进入，所以分支总数为结点总数减去 1。图 6-6-1 就是 9 个分支。对于 A、B、C、D 结点来说，它们都有两个分支线出去，而E结点只有一个分支线出去。所以总分支线为 4x2+1x1=9。

用代数表达就是分支线总数=n-1=n1+2n2。因为刚才我们有等式 n=n0+n1+n2，所以可推导出 n0+n1+n2-1=n1+2n2。结论就是 n0=n2+1。

6.6.4 二叉树性质 4

性质 4：具有 n 个结点的完全二叉树的深度为 [log2n]+1([x] 表示不大于 x 的最大整数)。

由满二叉树的定义我们可以知道，深度为 k 的满二叉树的结点数 n 一定是 2^(k)-1。因为这个最多的结点个数。那么对于 n=2^(k)-1 倒推得到满二叉树的度数为 k=log2（n+1），比如结点数为 15 的满二叉树，度为 4。

完全二叉树我们前面已经提到，它是一棵具有 n 个结点的二叉树，若按层序编号后其编号与同样深度的满二叉树中编号结点在二叉树位置完全相同，那它就是完全二叉树。也就是说，它的叶子结点只会出现在最下面的两层。

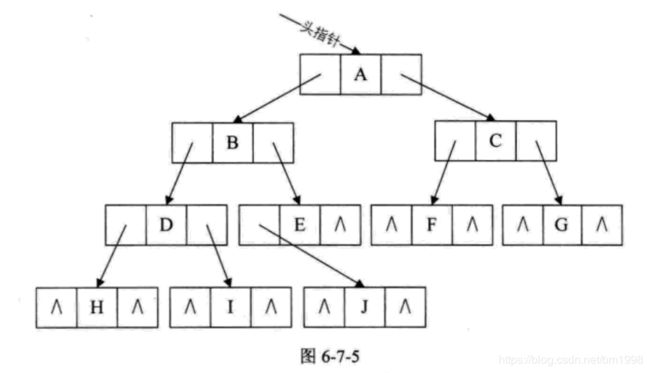
它的结点数一定少于等于同样度数的满二叉树的结点数 2^(k)-1，但一定多于 2^(k-1)-1。即满足 2^(k-1)-1(k)-1。由于结点数 n 是整数，n<=2^(k)-1 意味着 n<2^(k)，n>2^(k-1)-1，意味着 n>=2^(k-1)，所以 2^(k-1)<=n<2^(k)，不等式两边取对数，得到 k-1<=log2n

6.6.5 二叉树性质 5

性质 5：如果对一棵有 n 个结点的完全二叉树（其深度为 [log2n]+1）的结点按层序编号（从第一层到第 [log2n]+1 层，每层从左到右），对任一结点 i(1<=i<=n) 有：

1. 如果 i=1，则结点 i 是二叉树的根，无双亲；如果 i>1，则其双亲是结点 [i/2]。
2. 如果 2i>n，则结点 i 无左孩子（结点 i 为叶子结点）；否则其左孩子是结点 2i。
3. 如果 2i+1>n，则结点 i 无右孩子；否则其右孩子是结点 2i+1。

我们以图 6-6-2 为例，来理解这个性质。这是一个完全二叉树，度为 4，结点总数是 10。

• 对于第一条来说是很显然的，i=1 时就是根结点。i>1 时，比如结点 7，它的双亲就是 [7/2]=3，结点 9，它的双亲就是 [9/2]=4。
• 第二条，比如结点 6，因为 2x6=12 超过了结点总数 10，所以结点 6 无左孩子，它是叶子结点。同样，而结点 5，因为 2x5=10 正好是结点总数 10，所以它的左孩子是结点 10。
• 第三条，比如结点 5，因为 2x5+1=11，大于结点总数 10，所以它无右孩子。而结点 3，因为 2x3+1=7 小于 10，所以它的右孩子是结点 7。

6.7 二叉树的存储结构

6.7.1 二叉树顺序存储结构

前面我们已经谈到了树的存储结构，并且谈到了顺序存储对树这种一对多的关系结构实现起来是比较困难的。但是二叉树是一种特殊的树，由于它的特殊性，使得用顺序存储结构也可以实现。

二叉树的顺序存储结构就是用一维数组存储二叉树中的结点，并且结点的存储位置，也就是数组的下标要能体现结点之间的逻辑关系，比如双亲与孩子的关系，左右兄弟的关系等。

先来看看完全二叉树的顺序存储，一棵完全二叉树如图 6-7-1 所示。

将这棵二叉树存入到数组中，相应的下标对应其同样的位置，如图 6-7-2 所示。

这下看出完全二叉树的优越性来了吧。由于它定义的严格，所以用顺序结构也可以表现出二叉树的结构来。

当然对于一般的二叉树，尽管层序编号不能反映逻辑关系，但是可以将其按完全二叉树编号，只不过，把不存在的结点设置为 “^” 而已。如图 6-7-3，注意浅色结点表示不存在。

考虑一种极端的情况，一棵深度为 k 的右斜树，它只有 k 个结点，却需要分配 2^(k)-1 个存储单元空间，这显然是对存储空间的浪费，例如图 6-7-4 所示。所以，顺序存储结构一般只用于完全二叉树。

6.7.2 二叉链表

既然顺序存储适用性不强，我们就要考虑链式存储结构。二叉树每个结点最多有两个孩子，所以为它设计一个数据域和两个指针域，我们称这样的链表叫做二叉链表。结点结构图如表 6-7-1 所示。

其中 data 是数据域，lchild 和 rchild 都是指针域，分别存放指向左孩子和右孩子的指针。

以下是我们的二叉链表的结点结构定义代码。

/* 二叉树的二叉链表结点结构定义 */
typedef struct BiTNode //结点结构
{
	TElemType data; //结点数据
	struct BiTNode *lchild, *rchild; //左右孩子指针
}BiTNode,*BiTree;

结构示意图如图 6-7-5 所示。

就如同树的存储结构中讨论的一样，如果有需要，还可以再增加一个指向其双亲的指针域，那样就称之为三叉链表。由于与树的存储结构类似，这里就不详述了。