数据挖掘是从大型数据库中提取有趣的信息或模式。KDD过程又包括了数据清理、数据集成、数据选择与变换、数据挖掘以及模式评估和知识表示。其中关联规则挖掘是比较常见和贴近现实的一种。
关联规则挖掘的一个典型例子是购物篮分析。该过程通过发现顾客放入其购物篮中不同商品之间联系,分析顾客的购买习惯。通过了解哪些商品频繁地被顾客同时购买,这种关联的发现 可以帮助零售商制定营销策略。最经典的啤酒与尿布的营销案例。
关联规则挖掘
设 I = { i1 , i2 ,..., im }是项的集合。
设任务相关的数据 D 是数据库事务的集合,其中每个事务 T 是项的集合,使得 T ⊆ I。
设 A 是一个项集,事务 T 包含 A 当且仅当 A ⊆ T。关联规则是形如 A ⇒ B 的蕴涵式,其中 A ⊂ I,B ⊂ I,并且 A ∩ B = ∅。规则 A ⇒ B 在事务集 D 中成立,具有支持度 s, 规则 A ⇒ B 在事务集 D 中具有置信度 c。
即这条关联规则的支持度: support (A ⇒ B ) = P(A ∪ B)
关联规则的置信度: confidence (A ⇒ B ) = P(B|A)
同时满足小支持度阈值(min_sup)和小置信度阈值(min_conf)的规则称作强规则。为方便计, 我们用 0%和 100%之间的值,而不是用 0 到 1 之间的值表示支持度和置信度;
强关联规则就可以用来了解项之间的隐藏关系。所以关联分析的主要目的就是为了寻找强关联规则,而Apriori算法则主要用来帮助寻找强关联规则。
下面补充几个基本概念:
1.项集:项的集合称为项集。包含 k 个项的项集称为 k-项集。
2.项集频率:项集的出现频率是包含项集的事务数,简称为项集的频率、支持计数或计数。
3.频繁项集:项集满足小支持度 min_sup,如果项集的出现频率大于或等于 min_sup 与 D 中事务总数的乘积。如果项集满足小支持度,则称它为频繁项集。
频繁 k -项集的集合通常记作 Lk。
关联规则的挖掘是一个两步的过程:
1. 找出所有频繁项集:根据定义,这些项集出现的频繁性至少和预定义的小支持计数一样。
2. 由频繁项集产生强关联规则:根据定义,这些规则必须满足小支持度和小置信度。
Apriori算法
使用候选项集找频繁项集
Apriori算法是一种基于挖掘布尔关联规则频繁项集的算法。 算法使用频繁项集性质的先验知识(priori即有先验之意),正如我们将看到的。Apriori 使用一种称作逐层搜索的迭代方法, k-项集用于探索(k+1)-项集。首先,找出频繁 1-项集的集合。该集合记作 L1。L1 用于找频繁 2-项集 的集合 L2,而 L2用于找 L3,如此下去,直到不能找到频繁k-项集。找每个Lk需要一次数据库扫描。
为提高频繁项集逐层产生的效率,一种称作 Apriori 性质的重要性质用于压缩搜索空间。我们先介绍该性质,然后用一个例子解释它的使用。
Apriori 性质:频繁项集的所有非空子集都必须也是频繁的。根据 定义,如果项集 I 不满足小支持度阈值 s,则 I 不是频繁的,即 P(I) < s。如果项 A 添加到 I,则结果项集(即,I ∪ A)不可能比 I 更频繁出现。因此,I ∪ A 也不是频繁的,即 P(I ∪ A) < s。 该性质属于一种特殊的分类,称作反单调,意指如果一个集合不能通过测试,则它的所有超集也都不能通过相同的测试。称它为反单调的,因为在通不过测试的意义下,该性质是单调的。
下面的两步过程由连接和剪枝组成。
1. 连接步:为找 Lk,通过 Lk - 1与自己连接产生候选 k-项集的集合。该候选项集的集合记作 Ck。设 l1和 l2是 Lk - 1中的项集。记号 li[j]表示 li的第 j 项(例如,l1[k-2]表示 l1的倒数第 3 项)。为方便计,假定事务或项集中的项按字典次序排序。执行连接 Lk - 1 Lk - 1;其中,Lk - 1的元素是可连接的,如果它们前(k-2)个项相同;即,Lk - 1的元素 l1和 l2是可连接的,如果(l1 [1] = l2 [1]) ∧ (l1 [2] = l2 [2]) ∧ ... ∧ (l1 [k-2] = l2 [k-2]) ∧ (l1 [k-1] < l2 [k-1])。条件(l1 [k-1] < l2 [k-1])是简单地保证不产生重复。连接 l1和 l2产生的结果项集是 l1 [1] l1 [2]... l1 [k-1] l2 [k-1]。
2. 剪枝步:如何剪枝?就是根据上面说到的Apriori性质。候选集的每一条记录T,如果它的支持度小于最小支持度(min_sup),那么就会被剪掉;此外,如果一条记录T,它的子集有不是频繁集的,也会被剪掉。这种子集测试可以使用所有频繁项集的散列树快速完成。
看一个具体的例子,为了方便直观说明,参见了《数据挖掘:概念与技术》一书的示例:
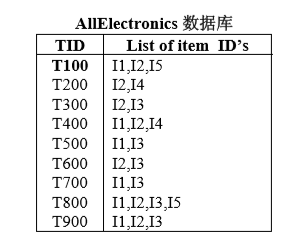
设最小事务支持度计数为2(即,min_sup=2/9),初始数据集如下图。
1.第一次迭代,每个项都是候选 1-项集的集合 C1的成员。算法简单地扫描所有的事务, 对每个项的出现次数计数。
2. 根据最小事务支持计数(或者说min_sup)。可以确定频繁 1-项集的集合 L1。它由 具有小支持度的候选 1-项集组成。
3.由L1产生C2。
4.扫描D中事务,计算C2中每个候选集的支持计数。
5. 确定频繁 2-项集的集合 L2,它由具有小支持度的 C2中的候选 2-项集组成。
6.由L2产生C3;
1).连接步:C3 = {{I1,I2,I3},{I1,I2,I5},{I1,I3,I5},{I2,I3,I4},{I2,I3,I5},{I2,I4,I5}}
2).剪枝步:频繁项集的所有子集必须是频繁的。
{I1,I2,I3}的 2-项子集是{I1,I2},{I1,I3}和{I2,I3}。{I1,I2,I3}的所有 2-项子集都是L2的元素。因此,保留{I1,I2,I3}在 C3中。
ƒ{I1,I2,I5}的 2-项子集是{I1,I2},{I1,I5}和{I2,I5}。{I1,I2,I5}的所有 2-项子集都是L2的元素。因此,保留{I1,I2,I5}在 C3中。 ƒ
{I1,I3,I5}的 2-项子集是{I1,I3},{I1,I5}和{I3,I5}。{I3,I5}不是 L2的元素,因而不是频繁的。删除{I1,I3,I5}。 ƒ
{I2,I3,I4}的 2-项子集是{I2,I3},{I2,I4}和{I3,I4}。{I3,I4}不是 L2的元素,因而不是频繁的。删除{I2,I3,I4}。 ƒ
{I2,I3,I5}的 2-项子集是{I2,I3},{I2,I5}和{I3,I5}。{I3,I5}不是 L2的元素,因而不是频繁的。删除{I2,I3,I5}。
{I2,I4,I5}的 2-项子集是{I2,I4},{I2,I5}和{I4,I5}。{I4,I5}不是 L2的元素,因而不是频繁的。删除{I2,I3,I5}
3).剪枝后的 C3 = {{I1,I2,I3},{I1,I2,I5}}。
由频繁项集产生关联规则
一旦由数据库 D 中的事务找出频繁项集,只需再验证关联规则是否满足最小置信度。对于置信度,可以用下式,其中条件概率用项集支持度计数表示。
confidence(A⇒B) = support_count(A∪B ) / support_count(A)
其中,support_count(A∪B)是包含项集 A∪B 的事务数,support_count(A)是包含项集 A 的事务数。根据该式,关联规则可以产生如下:
1.对于每个频繁项集 l,产生 l 的所有非空子集。
2.对于 l 的每个非空子集 s,如果support_count(l) / support_count(s) ≥ min_conf ,则输出规则“s ⇒ (l-s)”。其中,min_conf 是最小置信度阈值。
还是继续着上面的示例:
对于频繁项集{I1, I2, I5},可以由 l 产生哪些关联规则?
l 的非空子集有{I1,I2}, {I1,I5}, {I2,I5}, {I1}, {I2}和 {I5}。结果关联规则如下,每个都列出置信度。
I1∧I2 ⇒ I5, confidence = 2/4 = 50%
I1∧I5 ⇒ I2, confidence = 2/2 = 100%
I2∧I5 ⇒ I1, confidence = 2/2 = 100%
I1 ⇒ I2∧I5, confidence = 2/6 = 33%
I2 ⇒ I1∧I5, confidence = 2/7 = 29%
I5 ⇒ I1∧I2, confidence = 2/2 = 100%
如果小置信度阈值为 70%,则只有 2、3 和后一个规则可以输出。