《编程之美》学习笔记——2.13子数组的最大乘积

一、问题

  给定一个长度为N的整数数组，只允许使用乘法，不能用除法，计算任意(N-1)个数的组合乘积中最大的一组，并写出算法的时间复杂度。

分析：

输入：长度为N的整数数组array。

输出：(N-1)个数的组合最大乘积multiple。

约束：不能用除法计算。（如果可以使用除法，那么先求得N个整数数组的乘积，再遍历每个元素做除法运算即可求解，时间复杂度为O(n)）

二、解法

  解法一 暴力求解法 -> 空间换时间

思路：最简单的解法是遍历每一种组和求解，共有N种组合，对于每个组合都需要做(N-1)次乘法运算，因此时间复杂度为O(n^2)。

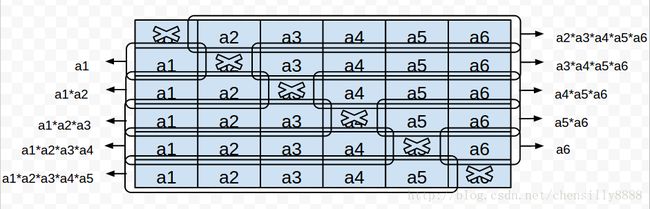
改进：考虑到大量的重复乘法工作，可以利用空间换时间，把重复的乘法工作利用最小的运算次数求得并把结果存储到一片内存中，然后再利用这些结果计算求解，减少大量的重复计算工作。对于这道题，假设数组长度为6，元素分别为a1，a2，a3，a4，a5，a6，如下图所示，要求(N-1)个数的所有组合的乘积，只需把下面每一行中左右两个圆角框内的结果相乘即可得到（首行和末行较特殊，乘积即单个框结果）。圆角框可描述为数组连续前i个数或后i个数的乘积。由于上下相邻的圆角框内的结果是只差一个乘积值，因此可用O(lgn)时间复杂度求得这些圆角框结果，利用圆角框的结果求最终解时也需O(lgn)时间复杂度。

时间复杂度：O(n)。

算法C实现：

上面圆角框结果采用两个数组存储，一个计算连续前n个数的乘积结果，头元素为1；一个计算连续后n个数的乘积结果，尾元素为1。（求取时从头至尾，从尾至头扫描数组两次）

/**
 * @brief find the subarray the max multipulation using more memory space.
 * the subarray with length n - 1 from input array with length n.
 *
 * @param[in,out]  array  array
 * @param[in]      count  array length
 *
 * @return the max multipulation
 */
ElementType find_subarray_max_multipulation(ElementType* array,
        CommonType count)
{
    assert(array != NULL && count > 1);
    CommonType i;
    ElementType temp, max_mutipulation = INT_MIN;
    /// memory space to save temp multipulation result
    ElementType* head_multiple = SMALLOC(count, ElementType);
    ElementType* tail_multiple = SMALLOC(count, ElementType);
    /// get head multipulation result
    head_multiple[0] = 1;
    for (i = 1; i < count; i++)
        head_multiple[i] = head_multiple[i - 1] * array[i - 1];
    /// get tail multipulation result
    tail_multiple[count - 1] = 1;
    for (i = count - 2; i >= 0; i--)
        tail_multiple[i] = tail_multiple[i + 1] * array[i + 1];
    /// get max multipulation result
    for (i = 0; i < count; i++) {
        if ((temp = head_multiple[i] * tail_multiple[i]) > max_mutipulation)
            max_mutipulation = temp;
    }
    return max_mutipulation;
}

  解法二 数学分析/数学规律

思路：我们利用数学分析对这道题求解，考察N个数的乘积P的正负性快速判断并剔除掉其中一个元素，从而留下的N-1个元素乘积即为问题的解。

1.P = 0，那么数组含0，假设去除1个0后的其他(N-1)个数乘积为Q：

  1.Q = 0：那么整个数组含有至少2个非零数，解为0；

  2.Q > 0：解为Q；

  3.Q < 0：解为0；

2.P > 0，那么数组可能含有偶数个或0个负数，且数组不含0：

  剔除掉最小的正数，剩下的N-1个数的乘积即为问题的解；

3.P < 0，那么数组含有奇数个负数，且数组不含0：

  剔除掉最大的负数（即绝对值最小的负数），剩下的N-1个数的乘积即为问题的解；

另外，判断P的正负性我们不必要求解这个乘积再来获得，可以统计数组大于0，等于0和小于0的元素个数来判断，避免了乘法运算，这些数据也可以用于Q的正负性判断。

（直接求N个数的乘积P在在编译环境下往往会有溢出的危险（这也是本题不使用除法的潜在用意）（摘自《编程之美》））

综上，求解步骤如下：

1.先遍历一遍数组，统计数组中大于0、小于0以及等于0的元素个数，并找到最大的负数和最小的正数；

2.通过上面分析思路，找到剔除的元素，再遍历一次数组求解最大乘积（实现时需注意可能存在多个最大负数或最小正数情况）。

时间复杂度：O(n)。

算法C实现：

/**
 * @brief find the subarray the max multipulation using math method.
 * the subarray with length n - 1 from input array with length n.
 *
 * @param[in,out]  array  array
 * @param[in]      count  array length
 *
 * @return the max multipulation
 */
ElementType find_subarray_max_multipulation(ElementType* array,
        CommonType count)
{
    assert(array != NULL && count > 1);
    CommonType i, flag_exclude = 0;
    CommonType positive_count = 0, negative_count = 0, zero_count = 0;
    ElementType max_mutipulation = 1;
    ElementType min_positive = INT_MAX, max_negative = INT_MIN;
    /// search needed math information from the array
    for (i = 0; i < count; i++) {
        /// count the positive, negative, zero value numbers
        /// get the minimum positive value and maximum negative value
        if (array[i] > 0) {
            positive_count++;
            if (min_positive > array[i])
                min_positive = array[i];
        } else if (array[i] < 0) {
            negative_count++;
            if (max_negative < array[i])
                max_negative = array[i];
        } else {
            zero_count++;
        }
    }
    /// get max multipulation by math analysis
    if (zero_count > 0) {
        if (zero_count > 1 || (negative_count & 0x01)) {
            max_mutipulation = 0;
        } else {
            /// exclude 0 element
            for (i = 0; i < count; i++) {
                if (array[i])
                    max_mutipulation *= array[i];
            }
        }
    } else if (negative_count & 0x01) {
        /// exclude a maximum negative element
        for (i = 0; i < count; i++) {
            if (array[i] == max_negative && !flag_exclude) {
                flag_exclude = 1;
                continue;
            }
            max_mutipulation *= array[i];
        }
    } else {
        /// exclude a minimum positive element
        for (i = 0; i < count; i++) {
            if (array[i] == min_positive && !flag_exclude) {
                flag_exclude = 1;
                continue;
            }
            max_mutipulation *= array[i];
        }
    }
    return max_mutipulation;
}

三、总结

  要善用元素的正负性判断、是否为零判断求解一些最值问题。