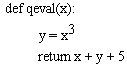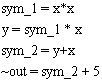hi 欢迎来到小秘课堂第三期,今天我们来讲讲白话零知识证明(二)的那些事儿,欢迎主讲人马宇峰
讲师:马宇峰
编辑:Leo
前言
本文是建立在 Vitalik 的博客《Quadratic Arithmetic Programs: from Zero to Hero》基础之上,加上一点点自己的理解写成的。相信许多小伙伴和我一样,在阅读各种关于 zk-SNARK 的论文和博客过程中,都曾被 QAP 搞得一头雾水,Vitalik 这篇博客的厉害之处就在于他把计算问题转换为 R1CS,再把 R1CS 转换成 QAP 问题的过程描述的很清楚。
QAP问题
首先,zk-SNARK 不能直接用于解决任何计算问题,我们必须先把问题转换成正确的“形式”来处理,这种形式叫做 "quadratic arithmetic problem"(QAP),在进行 QAP 转换的同时,如果你有代码的输入就可以创建一个对应的解(有时称之为 QAP 的 witness)。之后,还需要一个相当复杂的步骤来为 witness 创建实际的“零知识证明”,此外还有一个独立的过程来验证某人发送给你的证明。
举例说明
我们来选择一个简单的例子来做说明:证明你知道一个立方方程的解:
![]()
(提示:解是 3,解用来构造 witness)。这个例子既可以让你理解 zk-SNARK 背后的技术原理,又不会产生出很大的 QAP.
首先我们将这个方程用一种特殊的程序语言来表达
我们这里所使用的特殊的程序语言支持基本算术运算 (+,-,*,/),常量阶指数运算(如:可以计算 ![]() 但是不能计算
但是不能计算 ![]() ) 和变量赋值,理论上可以在这个语言中做任意计算(只要计算步骤的次数是受限制的,此外,不允许循环)。注意,这个语言不支持模运算 (%) 和比较运算 (<, >, <=, >=),但是通过提供辅助输入可以扩展到支持这两种运算,此处我们不做展开。
) 和变量赋值,理论上可以在这个语言中做任意计算(只要计算步骤的次数是受限制的,此外,不允许循环)。注意,这个语言不支持模运算 (%) 和比较运算 (<, >, <=, >=),但是通过提供辅助输入可以扩展到支持这两种运算,此处我们不做展开。
下一步是“拍平”(Flattening),我们要将刚才的代码转换成一系列只包含以下两种形式的声明
1:x = y ( y 可以是变量或者数字)
2:x = y op z ( op 是二元运算符,可以是 (+, - , *, /) 运算,y,z 可以是变量,数字或者子表达式 )
“拍平”后的结果是:
你可以认为上述的每一行声明都是一个电路中的逻辑门,与原始代码相比,这里我们引入了两个中间变量 sym_1 和 sym_2,还有一个表示输出的冗余变量 ~out,不难看出 “拍平” 后的声明序列和原始代码是等价的。
接下来我们要把上述结果转化成R1CS(rank-1 constraint system,一阶约束系统)
R1CS 是一个由三向量组 (a,b,c) 组成的序列,R1CS 有个解向量 s,s 必须满足,符号表示向量的内积运算。这里的解向量 s 就是 witness。举个例子:
a = (5,0,0,0,0,1),
b = (1,0,0,0,0,0),
c = (0,0,1,0,0,0),
s = (1,3,35,9,27,30),
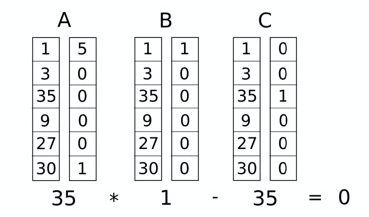
是一个满足的 R1CS,通过下图可以更直观的看出运算过程:
上述例子只有一个约束,接下来我们要将每个逻辑门 (即“拍平”后的每一个声明语句) 转化成一个约束(即一个三向量组),转化的方法取决于声明是什么运算 (+,-,*,/) 和声明的参数是变量还是数字。
在我们这个例子中,除了“拍平”后的五个变量 ('x', '~out', 'sym_1', 'y', 'sym_2') 外,还需要在第一个分量位置处引入一个冗余变量 ~one 来表示数字 1,就我们这个系统而言,一个向量所对应的 6 个分量是 (可以是其他顺序,只要对应起来即可):
'~one',' x', '~out', 'sym_1', 'y', 'sym_2' 解向量是以这个顺序对这些变量所赋的值。
通常,我们得到的向量都是稀疏的,现在我们给出第一个门![]()
![]() 的三向量组 (a,b,c):
的三向量组 (a,b,c):
'~one', ' x', '~out', 'sym_1', 'y', 'sym_2'
a = [0, 1, 0, 0, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 1, 0, 0]
可以看出如果解向量s的第二个标量是 3,第四个标量是 9,无论其他标量是多少,都有![]()
,同样,如果 s 的第二个标量是 7,第四个标量是 49,也会通过检查,第一次检查仅仅是为了验证第一个门的输入和输出的一致性。
类似的第二个门 ![]()
![]() 的三向量组 (a,b,c) 为:
的三向量组 (a,b,c) 为:
'~one', ' x', '~out', 'sym_1', 'y', 'sym_2'
a = [0, 0, 0, 1, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 0, 1, 0]
第三个门 ![]()
![]() 的三向量组 (a,b,c) 为:
的三向量组 (a,b,c) 为:
'~one', ' x', '~out', 'sym_1', 'y', 'sym_2'
a = [0, 1, 0, 0, 1, 0]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 0, 0, 0, 1]
加法的转化方式略有不同,我们应该理解为 (x + y)*1 - sym_2 类似的,最后一个门 ![]()
![]() 的三向量组 (a,b,c) 为:
的三向量组 (a,b,c) 为:
'~one', ' x', '~out', 'sym_1', 'y', 'sym_2'
a = [5, 0, 0, 0, 0, 1]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 1, 0, 0, 0]
好了,我们现在已经做了最后一次验证:
~out = sym_2 + 5.
witness(即解向量)是 [1,3,35,9,27,30]。(因为我们知道 x=3,将它带入“拍平”后的声明语句就可得到其他变量的解)。
现在我们得到了四个约束的 R1CS,完整的 R1CS 如下:
A
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 1, 0]
[5, 0, 0, 0, 0, 1]
B
[0, 1, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
C
[0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 1, 0]
[0, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 0, 0]
接下来我们要做的是将R1CS转化成QAP形式
这两者的区别是 QAP 使用多项式来代替点积运算,他们所实现的逻辑完全相同。在介绍这种转化之前,我们需要学习拉格朗日差值公式,这个公式的作用是构造一个穿过指定点的多项式,Vitalik 的文章中用了很大的篇幅介绍这个公式的使用,在这里我直接给出拉格朗日插值公式:
通过 n 个点 ![]() 的 n-1 阶多项式为
的 n-1 阶多项式为
例如通过点 (1,3), (2,2), (3,4) 的多项式为:
好了,学会使用这个公式后可以继续我们的步骤了。现在我们要将四个长度为六的三向量组转化为六组多项式,每组多项式包括三个三阶多项式,我们在每个x点处来评估不同的约束,在这里,我们共有四个约束,因此我们分别用多项式在 x = 1,2,3,4 处来评估这四个向量组。现在我们使用拉格朗日差值公式来将 R1CS 转化为 QAP 形式。
我们先求出四个约束所对应的每个 a 向量的第一个值的多项式,也就是说使用拉格朗日插值定理求过点 (1,0), (2,0), (3,0), (4,0) 的多项式,类似的我们可以求出其余的四个约束所对应的每个向量的第i个值的多项式。结果如下:
A 多项式组
[-5.0, 9.166, -5.0, 0.833]
[8.0, -11.333, 5.0, -0.666]
[0.0, 0.0, 0.0, 0.0]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
[-1.0, 1.833, -1.0, 0.166]
B 多项式组
[3.0, -5.166, 2.5, -0.333]
[-2.0, 5.166, -2.5, 0.333]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
C 多项式组
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[-1.0, 1.833, -1.0, 0.166]
[4.0, -4.333, 1.5, -0.166]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
这些系数是升序排序的,例如上述第一个多项式是 0.833x3 - 5x2 +9.166x -5. 如果我们将 x=1 带入上述十八个多项式,可以得到第一个约束的三个向量 (0, 1, 0, 0, 0, 0), (0, 1, 0, 0, 0, 0), (0, 0, 0, 1, 0, 0), 类似的我们将 x = 2, 3, 4 带入上述多项式可以恢复出 R1CS 的剩余部分。
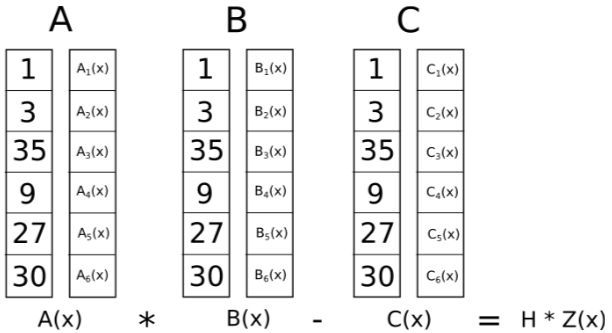
通过将 R1CS 转换成 QAP 我们可以通过多项式的内积运算来同时检查所有的约束而不是像 R1CS 那样单独的检查每一个约束。如下图所示:
我们需要检查结果多项式 A(x) * B(x) - C(x) 在 x=1,2,3,4 处是否都为 0,若在这四个点处有一处不为 0,那么验证失败,否则,验证成功。
根据代数学原理,正确性检查等价于结果多项式 A(x) * B(x) - C(x) 是否能够整除多项式 Z(x) = (x-1)(x-2)(x-3)(x-4). 不难看出多项式 Z(x) 是根据所有逻辑门约束条件所对应的点算出来的。通过这种等价形式的转化会大大减少我们的开销。
写到这里 zk-SNARK 的基本原理就算讲清楚了,后续都是一些优化过程,比如说我们的多项式系数是小数,这样会有舍入误差,在实际中我们会在有限域上做算术运算,这样结果都是整数,不存在舍入误差了。还有我们会将多项式验证转化为椭圆曲线上的双线性对运算来验证,这样可以进一步降低时间开销。
剩余部分
在完成我们的剩余部分前,我们需要先了解一些椭圆曲线对运算的知识,在这里我们仅介绍椭圆曲线对运算的一些性质,懂得这些性质就可以理解后续内容,有关椭圆曲线对运算的详细介绍,可以参考 Vitalik 的 blog。
关于椭圆曲线你需要知道以下知识:
1)椭圆曲线有一个 "生成点" G,G 做 n 次加法运算后可得到椭圆曲线上的所有点,n 称为椭圆曲线的阶。
2)当 d 足够大时,知道椭圆曲线上的两个点 P, Q 其中 Q = d*P,求 d 困难,这就是椭圆曲线上的离散对数问题。
设 P,Q,R,S 是椭圆曲线上的点,a,b 是整数,关于椭圆曲线对运算你需要知道以下性质:
1. e(aP, bQ) = e(P, Q)ab
2. e(P, Q+R) = e(P, Q)*e(P, R)
3. e(P+S, Q) = e(P, Q)*e(S, Q)
好,现在我们看看刚才学的知识的作用:如果你使用椭圆曲线上点 G 对一个数字 p 进行单项加密:
encrypt(p) = p*G = P,
椭圆曲线可以检查数字的线性组合,例如(大写字母表示椭圆曲线上的点,小写字母表示数字):
P = p*G, Q = q*G, R = r*G
检查
5*p + 7*q = 11 *r
相当于检查
5*P + 7*Q = 11 *R
这说明椭圆曲线具有同态性。
椭圆曲线上的对运算可以检查二次约束,例如:
检查
e(P, Q)*e(G, G*5)=1
相当于检查
p*q + 5 = 0.
目前为止我们已经了解了 QAP,可以将任何计算问题转化为多项式等式形式,这样可以更容易验证数学欺骗。此外我们也了解了椭圆曲线对运算,可以做等值验证。
下面我们要利用椭圆曲线对运算和其他的数学技巧来让证明者在不泄露解信息的情况下证明他知道一个 QAP 的解。
首先我们要引入KEA (指数知识假设, knowledge-of-exponent assumption)
在椭圆曲线上,KEA 指的是给定一对点 P, Q,其中 P*k = Q,然后在给定一个点 C,你不可能得到一个点 R = C *k,除非你知道 C 是怎样有点 P “派生” 出来的(例如,你知道 C = n*P 中的 n,那么 C*k=n*P*k=n*k*P=n*Q)。
以上是指数知识假设,zk-SNARK 的安全性依赖于这个假设,尽管 KEA 还没有被证明等价于其他困难问题(如离散对数问题),但是大多数密码学家认为它足够坚固。
下面我们看一下对椭圆曲线运算是怎样运用对运算的
假设现在有一对点 (P, Q) 其中 P*k = Q,没人知道 k 的值是什么,我得到这对点之后我给出一对新的点 (R, S) 并声称 R*k = S. 指数知识假设可以保证我能得到这对点的唯一途径是我用点 P 和 Q 同时乘以一个只有我自己知道的值 r. 通过椭圆曲线对运算的性质,我们可以在不需要知道 k 的情况下验证 R*k = S 是否成立:
e(R, Q) ?= e(P, S).
现在我们进一步给定十对点 (P1, Q1), (P2, Q2),...,(P10, Q10),每对点都有 Pi*k=Qi. 类似的,我给出一对新的点 (R, S) 并声称 R*k = S,这时可以推出我知道 R 是 P1,P2,...P10 的线性组合:
P1*i1+P2*i2+...+P10*i10,S 是点 Q1,Q2,...,Q10 使用同样系数的线性组合。我们可以使用同样的方法来验证 R*k = S.回顾一下我们刚刚讲的 QAP 的解是这种形式的:
A(x) * B(x) - C(x) = H(x) * Z(x).
其中:
多项式 A(X) 是多项式组 {A1(x), A2(x),..., A6(x)} 的线性组合;
多项式 B(X)是与 A(x) 相同系数的多项式组 {B1(x), B2(x),..., B6(x)} 的线性组合;
多项式 C(X) 是与 A(x) 相同系数的多项式组 {C1(x), C2(x),..., C6(x)} 的线性组合;
注意,在实际使用中多项式 A(X), B(X), C(X) 是很大的,可能会有上万个子项,因此证明者提供一个多项式的线性组合会很复杂。根据 Schwartz-Zippel 定理,两个 2d 阶(最高阶是 2d )多项式最多在 2d 个点处值相等,因此我们选一个随机值 t (由于我们所使用的有限域的阶远大于多项式的阶,因此找到另一个多项式使得这个多项式在t处取值和此多项式相等的概率小到可以忽略),来验证 A(t) * B(t) - C(t) ?= H(t) * Z(t) .
我们通过椭圆曲线上的对运算进一步降低计算量,设 G 是椭圆曲线的生成点(基点),证明者需要给出以下证明:
πA = G * A(t), πA' = G*A(t)*ka
πB = G * B(t), πB' = G*B(t)*kb
πC = G * C(t), πC' = G*C(t)*kc
πH = G * H(t)
验证者检查:
e(πA, πB)/e(πC, G)?=e(πH, G*Z(t))
到这里 zk-SNARK 的基本原理就讲完了,本文通过一个例子详细介绍了怎样将计算问题转化为 QAP形式,后面的部分写的有些简单,但是足够让大家理解 zk-SNARK 的基本原理。
关于讲师
马宇峰(Cris Ma)
秘猿科技研究院密码学研究员
秘猿科技 repo:https://github.com/cryptape
连接开发者与运营方的合作平台 CITAHub:https://www.citahub.com/
有任何技术问题可以在论坛讨论:https://talk.nervos.org
本文中涉及到的参考文献如下:
1.《Quadratic Arithmetic Programs: from Zero to Hero》
https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649
2.《Exploring Elliptic Curve Pairings 》
https://medium.com/@VitalikButerin/exploring-elliptic-curve-pairings-c73c1864e627
3.《Zk-SNARKs: Under the Hood 》
https://medium.com/@VitalikButerin/zk-snarks-under-the-hood-b33151a013f6