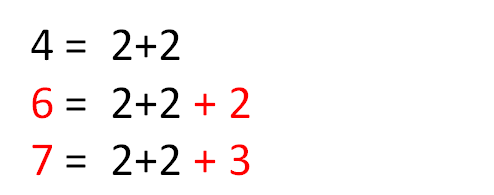漫画:什么是哥德巴赫猜想?
故事发生在小灰上小学的时候,有一天小灰向他的小学老师请教问题......
————————————
哥德巴赫猜想的起源
说起哥德巴赫猜想的起源,就不得不提到两个人,其中一位是业余数学家哥德巴赫,另一位是著名的大数学家欧拉。
首先让我们来回顾一下素数的含义:
所谓素数,就是除了1和它本身以外,无法被其他自然数所整除的数。比如 2,3,5,7,11,13,17,19......
话说有一天,哥德巴赫同学脑洞大开,发现有许多正整数都可以写成三个素数之和。
什么意思呢?让我们看几个例子:
整数9,可以写成 2+2+5
整数16,可以写成 2+7+7
整数30,可以写成2+11+17
那么,如何能证明,任何一个大于5的整数都可以写成三个素数之和?
哥德巴赫自己也想不出来,于是他写信询问他的朋友欧拉。
欧拉把哥德巴赫的命题做了如下转化:
任何一个大于2的偶数,都可以写成两个素数之和。
这又是什么意思呢?让我们再看几个例子:
偶数6,可以写成 3 + 3
偶数18,可以写成 5 + 13
偶数24,可以写成 5 + 19
“任何一个大于5的整数,都可以写成三个素数之和。”
“任何一个大于2的偶数,都可以写成两个素数之和。”
为什么说这两个命题等价呢?
简单地解释,把所有写成两素数之和的偶数再加上2或3,就可以表示一切大于5的正整数:
这样一个等价版本的命题,就成为了后世著名的哥德巴赫猜想。
什么是殆素数 ?
所谓殆素数,是指素数因子的个数不超过某一固定常数的正整数。
比如 15=3×5,有2个素数因子,我们可以说整数15是素数因子数量不超过2的殆素数。
再比如 45 = 3×3×5,有3个素数因子,我们可以说整数45是素数因子数量不超过3的殆素数。
而真正的素数,本身就只有1个素数因子。
想要一步到位证明哥德巴赫猜想,即“任何一大于2的偶数都可以写成两个素数之和”,恐怕并不太容易。那么我们不妨降低要求,首先证明任何一个大于2的偶数都可以写成两个殆素数之和,再一步一步向最终目标推进。
功夫不负有心人,1920年,有人成功证明了任何一个大于2的偶数都可以写成两个 “素数因子数量不超过9” 的殆素数之和,这个成果被简称为 “9+9”。
很快,更多的 “捷报” 陆续诞生:
1924年,“7 + 7” 被成功证明,即任何一个大于2的偶数都可以写成两个“素数因子数量不超过7” 的殆素数之和。
1932年,“6 + 6” 被成功证明。
1937年,“5 + 7”、“4 + 9” 被成功证明。
1938年,“5 + 5” 被成功证明。
1940年,“4 + 4” 被成功证明。
1956年,“3 + 4”、“3 + 3”、“2 + 3” 被成功证明。
1962年,“1 + 5”、 “1 + 4” 被成功证明。
1965年,“1 + 3” 被成功证明。
1966年,“1 + 2” 被成功证明,这一次的功臣是我国的著名数学家陈景润先生。
用最直白的语言来描述,陈景润证明了任何一个大于2的偶数都可以写成(素数A+素数B×素数C)或(素数A+素数B)的形式。
此时,关于哥德巴赫猜想的研究进展距离最终目标只有一步之遥!
而这个问题的终点,“任何一大于2的偶数都可以写成两个素数之和”,就是传说中的 “1+1”。
因此,这里的“1+1”指的是两个素数之和,千万不要把它理解成字面上的1+1=2,不然就丢人现眼了!
哥德巴赫猜想的未来
既然陈景润先生已经成功证明了 “1+2”,那么最终证明 “1+1” 岂不是手到擒来了?
很遗憾,一直到50多年后的今天,哥德巴赫猜想的终点 “1+1” 还是没有得到成功证明。
时至今日,有许许多多的 “民间数学家” 花费大量精力试图证明哥德巴赫猜想,他们对于数学世界的探索精神很值得赞赏。但是,由于缺乏起码的数学功底,他们的证明往往从根儿上就是错误的。
但是话说回来,我们也期望着有朝一日,哥德巴赫猜想能够被某个绝世的数学天才成功证明。
作者:小灰,本文经授权转自个人公众号「程序员小灰」,版权归其所有。