Python学习-机器学习实战-ch07 AdaBoost
终于完成答辩了,抓紧最后学生时光学习
----------------------------------------------------------------------------------
这章里书中首先介绍了几个概念:
一、元算法(meta-algorithm)
元算法也叫集成方法(ensemble method),其思想是使用其他算法进行组合,也是常说的“三个臭皮匠凑成一个诸葛亮”。AdaBoost是其中最流行的元算法。使用集成方法时可以有多种形式:可以是不同算法的集成,也可以是同一算法在不同设置下的集成,还可以是数据集不同部分分配给不同分类器的集成。
集成方法主要有两种:bagging方法和boosting方法。
bagging方法
自举汇聚法(boostrap aggregating),也称bagging方法。
Bagging的策略【来源】:
- 从样本集中用Bootstrap采样选出n个样本
- 在所有属性上,对这n个样本建立分类器(CART or SVM or ...)
- 重复以上两步m次,i.e.build m个分类器(CART or SVM or ...)
- 将数据放在这m个分类器上跑,最后vote看到底分到哪一类
bagging方法是一种从原始数据及选择S次后得到S个新数据集的一种技术。新数据集和原数据集的大小相等。每个数据集都是通过在原始数据集中随机选择一个样本进行替换而得到的。(替换的方法可以是随机选择一个样本,再随机选择一个样本替换。)所以,新数据集中可以存在重复的值,同时,原始数据集的部分值在新数据集中不再出现。bagging方法在S个数据集建好之后,将某个学习算法分别作用于每个数据集就得到了S个分类器。要对新数据进行分类时,就可以应用这S个分类器进行分类。选择分类器投票最多的类别作为分类结果。
-------【来源】--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
- Random forest(Breiman1999):
- 从样本集中用Bootstrap采样选出n个样本,预建立CART
- 在树的每个节点上,从所有属性中随机选择k个属性,选择出一个最佳分割属性作为节点
- 重复以上两步m次,i.e.build m棵CART
- 这m个CART形成Random Forest
boosting方法
boosting方法是一种用来提高弱分类器算法准确度的方法。boosting方法是一种用来提高弱分类算法准确度的方法,这种方法通过构造一个预测函数系列,然后以一定的方式将他们组合成一个预测函数。他是一种框架算法,主要是通过对样本集的操作获得样本子集,然后用弱分类算法在样本子集上训练生成一系列的基分类器。
与bagging方法相比,后者是不同分类器是通过串行训练而获得,每个分类器都根据已训练出的分类器的性能来进行训练。boosting方法是集中关注被已有分类器误分的数据来获得新的分类器。bagging方法的分类器的权重是相等的,boosting方法的分类器权重并不相等,每个权重代表其对应分类器在上一轮迭代中的成功度。
AdaBoost方法是boosting方法中最流行的一个。
优点:泛化错误率低,易编码,可以用在大部分的分类器上,无参数调整。
缺点:对离群点敏感。
AdaBoost是adaptive boosting的缩写,基本思想是由若干个弱分类器组合而成一个强分类器。“弱”意味着该分类器的性能只比随机猜测要略好,但也不会好太多。,其方法是:给训练数据中的每个样本赋予一个权重,初始时权重都是相等的。首先在训练数据上训练从一个弱分类器并计算分类器的错误率。对样本的权重进行修改,分类正确的样本权重会降低,分类错误的样本权重会提高。对权重修改后的样本再次训练出一个分类器。每个弱分类器自身也有一个权重值,由分类器的错误率决定。在更新样本的权重后进入下一次迭代。最终的强分类器由弱分类器加权求和而成。
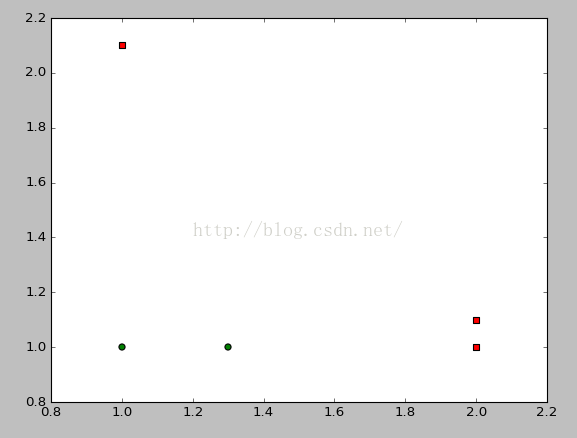
def loadSimpleData():
datMat=matrix([[1.,2.1],[2.,1.1],[1.3,1.],[1.,1.],[2.,1.]])
classLabel=[1.0,1.0,-1.0,-1.0,1.0]
return datMat,classLabel书中的可视化图有错误。
n=shape(dataMat)[0]
xcord1=[];ycord1=[]
xcord2=[];ycord2=[]
for i in range(n):
if int(classLabel[i])== 1:
xcord1.append(dataMat[i,0]);ycord1.append(dataMat[i,1])
else:
xcord2.append(dataMat[i,0]);ycord2.append(dataMat[i,1])
fig=plt.figure()
ax=fig.add_subplot(111)
ax.scatter(xcord1,ycord1,s=30,c='red',marker='s')
ax.scatter(xcord2,ycord2,s=30,c='green')
plt.show()可视化代码如上所示。
接着开始实现adaboost,首先使用单层决策树作为弱分类器。
def stumpClassify(dataMatrix,dimen,threshVal,threshIneq):
#函数在数据与阈值比较进行分类
retArray=ones((shape(dataMatrix)[0],1))
if threshIneq=='lt':
retArray[dataMatrix[:,dimen]<=threshVal]=-1.0
else:
retArray[dataMatrix[:,dimen]>threshVal]=-1.0
return retArray
这是一个简单的根据阈值进行分类的函数。
def buildStump(dataArr,classLabels,D):
#找到数据集上最佳单层决策树,D是数据对应的权重向量
dataMatrix=mat(dataArr)
labelMat=mat(classLabels).T
m,n=shape(dataMatrix)
#获得数据行列数
numSteps=10.0
#设置步数
bestStump={}
bestClassEst=mat(zeros((m,1)))
#初始化最佳
minError=inf
for i in range(n):
#遍历每个特征维度
rangeMin=dataMatrix[:,i].min()
rangeMax=dataMatrix[:,i].max()
stepSize=(rangeMax-rangeMin)/numSteps
#根据该特征的最大最小值设置步长
for j in range(-1,int(numSteps)+1):
#循环在步长上进行遍历
for inequal in ['lt','gt']:
threshVal=(rangeMin+float(j)*stepSize)
#根据步长设置阈值
predictedVals=stumpClassify(dataMatrix,i,threshVal,inequal)
#按照阈值分类,最简单的分类方法
errArr=mat(ones((m,1)))
errArr[predictedVals==labelMat]=0
#统计错误个数
weightedError=D.T*errArr
#错误样本的加权求和
print("split: dim %d, thresh %.2f, thresh inequal:%s, the weighted error is %.3f" %(i,threshVal,inequal,weightedError))
if weightedError一个简单版单层决策树函数。
构建完简单版的决策树节点作为弱分类器之后,开始在此基础上完成AdaBoost训练
def adaBoostTrainDS(dataArr,classLabels,numIt=40):
#adaboost函数,numIt表示迭代次数
weakClassArr=[]
m=shape(dataArr)[0]
#获得数据个数
D=mat(ones((m,1))/m)
#初始化权重,平均值
aggClassEst=mat(zeros((m,1)))
for i in range(numIt):
bestStump,error,classEst=buildStump(dataArr,classLabels,D)
#选择弱分类器
print("D:",D.T)
alpha=float(0.5*log((1.0-error)/max(error,1e-16)))
#alpha是每个弱分类器对应的权重
#此处max(error,1e-16)是防止error为0导致溢出
bestStump['alpha']=alpha
weakClassArr.append(bestStump)
#把当前弱分类器加入到弱分类器数组里
print("classEst:",classEst.T)
expon=multiply(-1*alpha*mat(classLabels).T,classEst)
#根据是否被错分是不一样的,分对权重低、分错权重高。
D=multiply(D,exp(expon))
D=D/D.sum()
#更新权重向量D,D表示样本的权重,根据是否被错分会进行调整
aggClassEst+=alpha*classEst
#每个数据点的类别累计值
print("aggClassEst:",aggClassEst.T)
aggError=multiply(sign(aggClassEst)!=mat(classLabels).T,ones((m,1)))
#累加错误
errorRate=aggError.sum()/m
print("total error:",errorRate,"\n")
if errorRate==0.0:break
#如果错误率为0也停止循环
return weakClassArr,aggClassEst这样就能完成AdaBoost的训练了,接着构造一个分类函数
def adaClassify(datToClass,classifierArr):
dataMatrix=mat(datToClass)
m=shape(dataMatrix)[0]
aggClassEst=mat(zeros((m,1)))
#对应的结果
for i in range(len(classifierArr)):
classEst=stumpClassify(dataMatrix,classifierArr[i]['dim'],\
classifierArr[i]['thresh'],classifierArr[i]['ineq'])
#由分类函数可以得到每个弱分类器的分类结果
aggClassEst+=classifierArr[i]['alpha']*classEst
#将每个结果加权求和得到最终的分类结果
print(aggClassEst)
return sign(aggClassEst)上述函数已经能够实现训练和分类功能了。下面在一个较难数据集上使用:
def loadDataSet(fileName):
numFeat=len(open(fileName).readline().split('\t'))
#获得特征的维数
dataMat=[]
labelMat=[]
fr=open(fileName)
for line in fr.readlines():
lineArr=[]
curLine=line.strip().split('\t')
for i in range(numFeat-1):
lineArr.append(float(curLine[i]))
dataMat.append(lineArr)
labelMat.append(float(curLine[-1]))
return dataMat,labelMatdef plotROC(predStrengths,classLabels):
import matplotlib.pyplot as plt
cur=(1.0,1.0)
ySum=0.0
numPosClas=sum(array(classLabels)==1.0)
#统计真正例个数
yStep=1/float(numPosClas)
#1/正例个数为Y轴步长
xStep=1/float(len(classLabels)-numPosClas)
#1/反例个数为X轴步长
sortedIndicies=predStrengths.argsort()
#argsort返回的是从小到大排列后的索引值
fig=plt.figure()
fig.clf()
ax=plt.subplot(111)
for index in sortedIndicies.tolist()[0]:
if classLabels[index]==1.0:
delX=0
delY=yStep
else:
delX=xStep
delY=0
ySum+=cur[1]
#划线时如果是正例,y轴改变,如果是反例,x轴改变。
ax.plot([cur[0],cur[0]-delX],[cur[1],cur[1]-delY],c='b')
#plot([x1,x2],[y1,y2])表示从(x1,y1)画到(x2,y2)
cur=(cur[0]-delX,cur[1]-delY)
#从右往左画
ax.plot([0,1],[0,1],'b--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
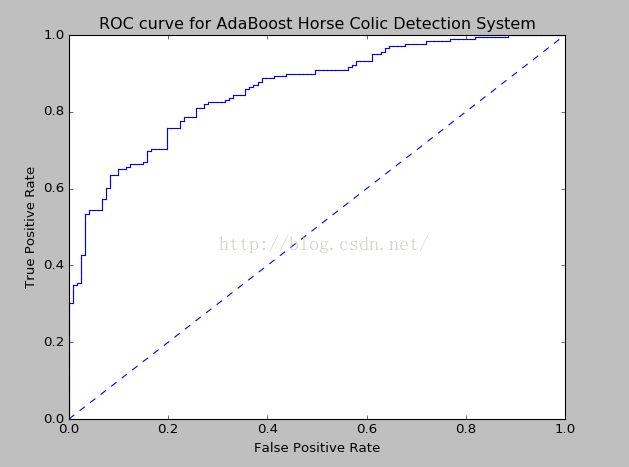
plt.title('ROC curve for AdaBoost Horse Colic Detection System')
ax.axis([0,1,0,1])
plt.show()
print('the Area Under the Curve is :',ySum*xStep)上面这个函数实现的是一个绘制ROC曲线的功能,ROC曲线的横轴是假阳率(=FP/(FP+TN)),纵轴是真阳率(=TP/(TP+FN))。至于TP、TN、FP、FN的概念就比较简单了。
TP和TN比较简单,T表示TRUE就是判断正确的意思。
那么FP和FN表容易搞错,F表示FALSE。既然是false,FP直译就是错误的正例。错误的正例是什么?就是一个反例啊。也就是一个反例被误判成了正例。同理,FN表示一个正例被误判成了反例。
FP+TN等同于数据集里真实的反例个数。TP+FN表示数据集里真实的正例个数。
本章对非均衡分类问题稍微提了一下,总结了处理非均衡问题的数据抽样方法:
除了对分类器进行调整,还可以从训练数据上下手。一般通过欠抽样或过抽样来实现。过抽样是通过复制样例,而欠抽样是删除样例。
例如,信用卡欺诈案例中,正例类别属于罕见类别,希望能对这种罕见类别尽可能多的保留更多的信息。所以,可以保留所有整理,欠抽样处理反例。但是这样的问题在于,无法确定哪些样例需要剔除。解决这个问题的方法可以是选择那些离决策边界较远的样例进行删除。但是,当正反例样本数量相差巨大时,需要另一种替代策略是使用反例类别的欠抽样和正例类别的过抽样混合的方法。正例样本进行过抽样可以通过复制已有样例或加入已有样例相似样本。一种是加入已有数据的插值点,但这种可能导致过拟合的问题。