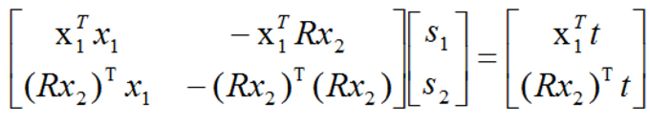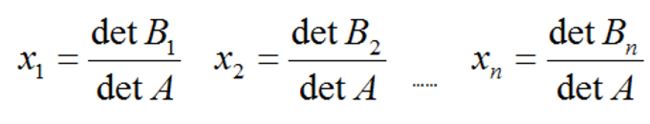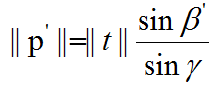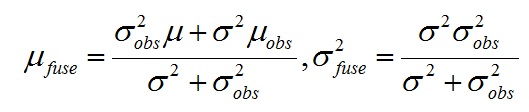三角测量恢复深度
(一)三角化得到深度值
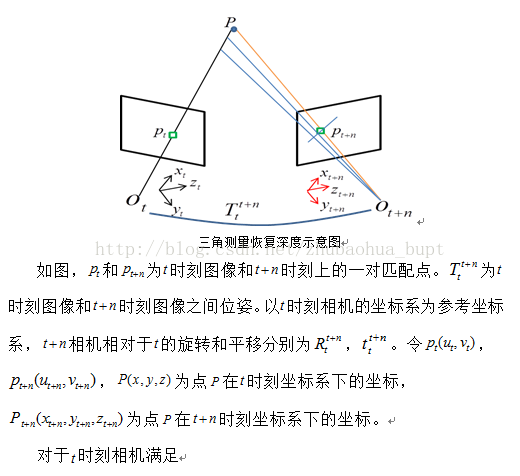
三角化恢复深度信息。目录:
(1)三角化的提出
(2)三角化公式
(3)求解深度的另外两种方法
(1)三角化的提出
三角化最早由高斯提出,并应用于测量学中。简单来讲就是:在不同的位置观测同一个三维点P(x, y, z),已知在不同位置处观察到的三维点的二维投影点X1(x1, y1), X2(x2, y2),利用三角关系,恢复出三维点的深度信息z。
(2)三角化公式
按照对极几何中的定义,设x1, x2为两个特征点的归一化坐标,则它们满足:
s1x1 = s2Rx2 + t 公式(1)
=> s1x1 - s2Rx2 = t 公式(2)
对公式(2)左右两侧分别乘以x1T,得:
s1x1Tx1 - s2x1TRx2 = x1T t 公式(3)
对公式(2)左右两侧分别乘以(Rx2)T,得:
s1(Rx2)Tx1 - s2(Rx2)TRx2 = (Rx2)T t 公式(4)
由公式(3)和公式(4)可以联立得到一个一元二次线性方程组,然后可以利用Cramer's法则(参见线性代数书)进行求解。
如下是对应的代码
(3)求解深度的另外两种方法
a.利用叉乘进行消元进行求解
由
s1x1 = s2Rx2 + t 公式(1)
左右两边同时乘以x1的反对称矩阵,可得:
s1x1^x1 = 0 = s2x1^Rx2 + x1^t 公式(2)
由上式可解得s2,
将s2代入公式(1),可求得s1
b.利用Mid Point Method进行求解(Hartley大名鼎鼎的《Multiple View Geometry》中有讲解)
从此图中我们可以知道,理想情况下O1P和O2P会相交于空间中的一点,但是由于图像分辨率以及噪声的存在,实际的情况更可能是上图所描述的那样:O1P和O2P在空间中没有交点,这时我们需要找到一个O1P与O2P之间的公垂线,然后取其上的中点作为我们重建出的三维点,此即为Mid Point Method,具体的推导及公式请参看Hartley的《Multiple View Geometry》。
好了,今天的三角化深度信息我们就讲解到这里,下次课我们接着讨论三角化深度信息中的误差分析。
附录:
1.Cramer's 法则:
如果A的行列式不为0, Ax=b可以通过如下行列式进行求解:
矩阵Bj为A的第j列被b替换后得到的新的矩阵。
(二)三角化深度值的误差分析
(1)三角化所带来的误差的提出
(2)三角化中误差的来源分析
(3)如何减小三角化所带来的误差
(4)三角化所遇到的奇异情况
(1)三角化所带来的误差的提出
两帧图像中的特征点坐标三角化得到空间点的三维信息。来分析一下三角化得到的三维信息中深度的误差。
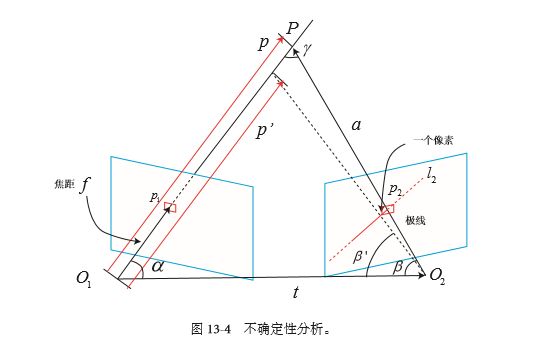
如上图所示:
P为空间中的一个三维点,p1和p2分别为在两个位置处,摄像机观察到的投影的二维点坐标。
l2为p1在第二幅图中所对应的极线(极线的概念请参考立体视觉中的对极几何,这里不再赘述)。
现在,我们要探讨的是:
如果我们在l2进行极线搜索时,所找到的p2'点与真实的p2点有一个像素的误差,那么会给三角化后的三维点P的深度z带来多大的误差。
首先,根据上图,我们可以得到向量之间的关系,以及三角化中的两个夹角的定义:
a = p - t 公式(1)
α = arccos
β = arccos
其中,a, p, t均为向量,α和β为图中所示的两个夹角。
如果此时,我们求取的p2'点与p2点有一个像素的偏差,同时,这一个像素的偏差又会给β带来δβ的角度变化,我们利用β'来表示对β进行δβ扰动后的新的角度。
设相机的焦距为f,则:
公式(4):
公式(5):
公式(6):
至此,加入扰动后的所有新的角度我们都求出来了。
由正弦定理,我们可以得到:
公式(7):
则由第二个位置上的二维点的一个像素的误差,可能导致的三角化后深度的误差为:
δp = ||p|| - ||p'||
这里的δp其实也正是深度的一个均方差(不确定度σobs),这个不确定度是我们后面要介绍的深度滤波器的一个很重要的概念,深度滤波器的目的也正是要不断减小这个不确定度,使得深度的不确定度最后能够收敛到一个能够接受的值。
(2)三角化中误差的来源分析
上面分析了第二幅图中的特征点p2的误差是如何影响三角化后的深度值的。
下面,我们来指出三角化的误差来源有哪几方面:
a.图像的分辨率:图像的分辨率越高,一个像素所带来的δβ就越小。
b.特征点求取时的精度:是否做到亚像素,在亚像素的基础上,误差有多大?
c.p1点的误差:会引起极线l2的误差,从而间接地影响p2点的精度。
d.相机两次位置的平移向量t的大小:t的模的大小也代表了对极几何中的基线长度,由公式(7)可以看出基线长度越大,三角化的误差越小。
(3)如何减小三角化所带来的误差
根据【(2)三角化中误差的来源分析】中所分析的一些因素可知,要想减小三角化过程中引入的误差,可以有如下几个方法:
a.选取尽可能高分辨率的相机。
b.进行亚像素的优化(比如在极线搜索时对像素点坐标进行双线性插值)
(关于双线性插值,这篇文章做了比较清晰的讲解:http://blog.163.com/guohuanhuan_cool@126/blog/static/167614238201161525538402/)
c.同样使用亚像素级的图像处理算法来处理p1点。
d.在不丢失特征点的情况下,让平移量t尽量大。
(4)三角化所遇到的奇异情况
由上面的公式推导我们可以看出,三角化中,必须要有平移量t,否则无法构成三角形,进行三角化。
所以在有些单目的SLAM,AR/VR的场景中,有经验的人都会有意识地将设备或者相机进行一定量的平移,而不会在原地进行纯旋转。
总结一下,我们今天分析了三角化过程中的误差有哪些,并从理论上对误差进行了量化的推导。同时,我们还分析了如何减小三角化过程中的误差。
(三)深度滤波器的原理及实现
一提到深度滤波器,大家肯定首先会觉得深不可测,听名字就觉得高大上。其实,有了前面的预备知识,不难理解今天要讲解的深度滤波器的原理。
我们今天给大家介绍的是比较简单的高斯分布假设下的深度滤波器。
高斯分布是自然界中最常见的一种分布形式,并且也符合绝大部分的自然情况。简单起见,我们先假设三角化后恢复的深度值符合高斯分布。对于像素点的深度值d,满足:
P(d) = N(μ,σ2)
每当新的数据过来,我们就要利用新的观测数据更新原有的深度d的分布。
这里的数据融合的方式与经典的Kalman滤波方式大同小异。
这里,我们利用观测方程进行信息融合。
假设新计算出来的深度数据的分布为:
P(dobs) = N(μobs,σobs2)
我们将新计算出来的深度数据乘在原来的分布上,进行信息融合的更新:
我们知道,利用两个高斯分布的乘积的分布公式,可以得到融合后的高斯分布:
P(dfuse) = N(μfuse, σfuse2)
其中,
那么问题来了,这里的μobs,σobs2该如何才能得到呢?
这里的μobs实际上就是每次我们新三角化出来的深度值,而对于σobs2,如果你还对上一篇文章有印象的话,就会记得我们推导了一系列公式所得到的那个δp(不确定度σobs),如果你忘记了,可以回去上一篇文章再复习一下。
那么原始的分布μ,σ2该如何得到呢?
这个很简单,第一次三角化出来的μ,σ2就可以作为初始值,然后每次新三角化出一个三维点,就去更新深度值的分布。
至此,我们似乎得到了一个不错的结果:既简单又优美的公式。
实际上还会存在什么问题呢?
(1)实际的深度值分布是否真的符合高斯分布?
(2)如果我们中间过程有一次三角化的过程求错了,并且还进行了信息融合,会有什么后果?
(3)我们如何避免第二个问题中所提出的情况?
这些问题留给读者去思考,也欢迎在下方给我留言,一起探讨这些问题的解决方案。