前言
首先,我将介绍这3个任务,它们以多项式的推导为中心,并且输出的目的是相同的。 换句话说,对输入多项式进行微分,并将求导结果打印在显示器上,从而增加了操作难度。 从简单的固定多项式到复杂的弹性多项式,放宽了要求,增加了导数难度。 从使用正则表达式解决所有问题到继承接口,处理的难度不断增加。 随着状态的引入,Java代码变得更加复杂,因此让我们分别分析这三个任务。
1、第一次作业
工作要求的简要说明:多项式推导通过将多个项目与加法和减法运算符连接而形成多项式,该运算符由有符号整数和幂乘积组成。 +1 + x的省略形式可能在多项式之前有一个符号,带符号整数之间没有空格,而在其他位置也有空格。 以上是对工作要求的改进。
解决作业问题的想法:这次,作业结构:
实施摘要:
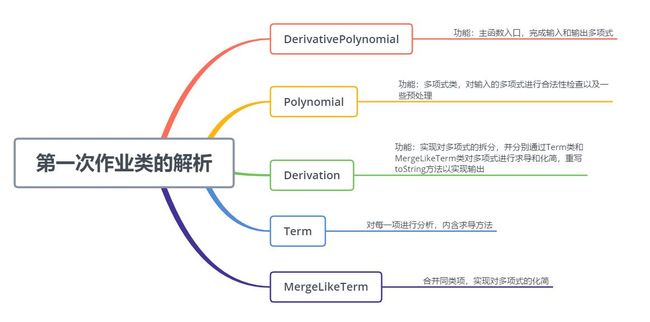
主要类是DerivationPolynomial,它提供函数输入,然后调用多项式以进行合法性检查。浏览字符串,检查无效字符,然后列出空格不正确的情况,最后进行大的常规匹配检查合法性后,从字符串中删除所有空格并合并多个符号
多项式类检查合法性,派生派生实例化派生,使用正则表达式捕获组单独提取字符串的每个项目,将其存储在数组中,然后编写Term类以提取Term类的每个项目。通过计算索引和符号,创建派生方法,返回派生结果以及实例化MergeLikeTerm类来执行多项式合并。合并算法非常简单。标记为无效的项目,重写为String类,输出标记为有效的项目
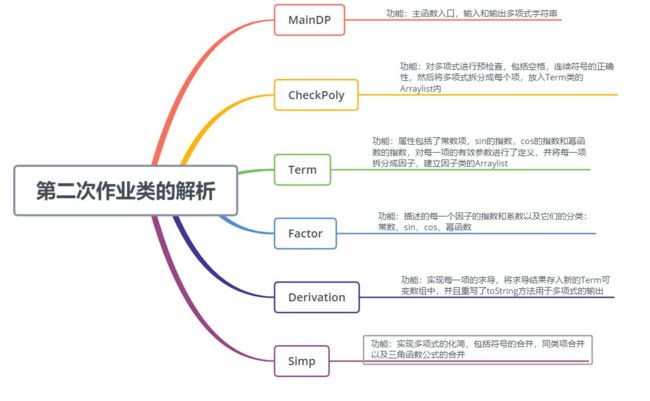
2、第二次作业作业要求简述:在第一次作业的基础上增加了三角函数sin(x)和cos(x),要求是三角函数保留字内不可以有空格,而且三角函数的参数里只能是x,不能是其他函数,除此之外,因子之间组合形式更加复杂,项可以是多个因子的乘积,而且第一个因子如果是1*的形式可以简写为+,-1*可以简写为-,其他要求和第一次相同作业解题思路:
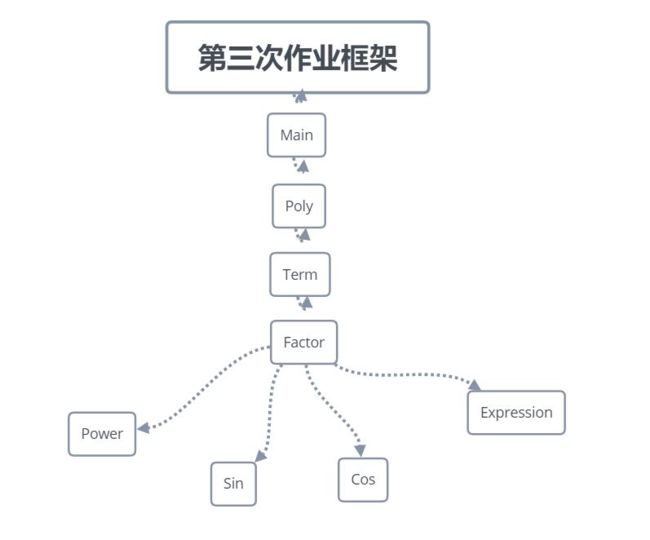
3、第三个作业的作业要求的简要说明:与前两个作业相比,第三个作业增加了多项式推导的难度,增加了三角函数的叠加,并增加了表达系数。 它是一个简单的常数,三角函数或平方幂函数,括号中的表达式可能会作为某些项目的因子出现,三角函数的参数不再是x,而可以是任何表达式。 它已经完成,并且我无法在指定的时间内实现基本功能,但是通用框架不是问题。 让我介绍一下我的框架。
二、心得
第一个单元的工作已经结束,对我作业难度比较大,我只能专心于学习java和oo思想,在此过程中,我发现我的思维漏洞(即对象封装)始终是不完整的,并且很容易将许多对象组合在一起,从而使它们之间的逻辑变得复杂且难以理解。 很难处理。 希望后续的作业可以跟上课程进度