【Python Deap库】遗传算法/遗传编程 进化算法基于python DEAP库深度解析讲解

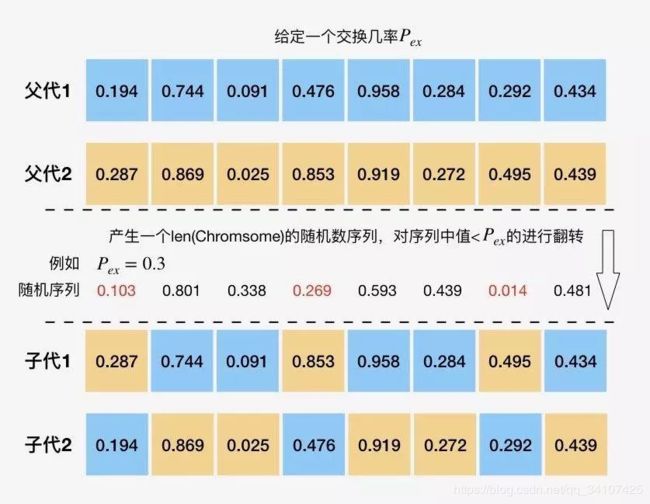
前言

看了很多，发现这个遗传算法，进化算法是一个非常有用的一个方法。而且可解释性远远强于神经网络。之前写了一篇博文，专门讲解基于DEAP库的python编程，来编写遗传算法，但是那一篇主要偏重代码，出于想要深入理解代码的含义，因此专门记下这篇博文，既是笔记，也是分享。

---

所有的用python实现的代码，请看这个博文：
GEAP 遗传算法/遗传编程 genetic programming + python(deap库)实现
如果需要还有这两个：
遗传算法GA和遗传编程GP有什么不同？
粒子群算法PSO 和 遗传算法GA 的相同点和不同点

---

概述

“物竞天择，优胜劣汰”， 达尔文提出了著名的生物进化理论，即所有的动植物都是由较早期、较原始的形式演变而来的。而遗传编程（遗传规划）则在数学和计算机科学领域应用了这一演化过程：从基数较为庞大的原始、粗糙的程序种群中通过评估适应性选择父系、进行遗传操作生成新一代种群，再判断终止条件决定是否再次迭代、生成下一代种群。类比如下：


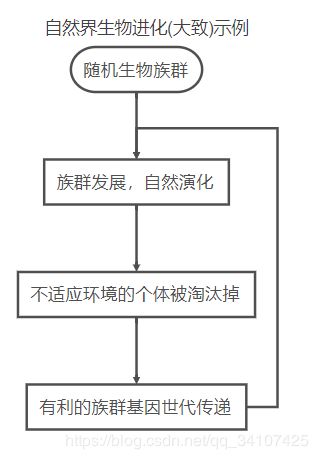
讲到这里可否理解了，进化算法的本质就是模拟优胜劣汰，下面进入正题

启发式的理解（重点）

整个包含以下几个方面！一定要看一下

1. 个体编码(Individual representation): 将问题的解空间编码映射到搜索空间的过程。常用的编码方式有二值编码(Binary)，格雷编码(Gray)，浮点编码(Floating-point)等。
   简单的说就是你怎么表示一个个体，使用01010101010101来表示一个个体，还是用1238583241来表示一个个体
2. 评价(Evaluation): 设定一定的准则评价族群内每个个体的优秀程度。这种优秀程度通常称为适应度(Fitness)。
   基于你的个体编码，判断你的个体编码好不好的一个评价函数
3. 配种选择(Mating selection): 建立准则从父代中选择个体参与育种。尽可能选择精英个体的同时也应当维护种群的多样性，避免算法过早陷入局部最优。
   你要选择哪些个体参与育种，也就是参与下面那一个环节
4. 变异(Variation): 变异过程包括一系列受到生物启发的操作，例如重组(Recombination)，突变(mutation)等。通过变异操作，父代的个体编码以一定方式继承和重新组合后，形成后代族群。
   保留下来的个体，进行重组，突变等等
5. 环境选择(Environmental selection): 将父代与子代重组成新的族群。这个过程中育种得到的后代被重新插入到父代种群中，替换父代种群的部分或全体，形成具有与前代相近规模的新族群。
   生下来的个体 按道理讲应该是比父类数量少的，一般都会补全到和父类的size相同，补全的方案就叫做环境选择
6. 停止准则(Stopping crieterion): 确定算法何时停止，通常有两种情况：算法已经找到最优解或者算法已经选入局部最优，不能继续在解空间内搜索。

---

咱们看个流程图理解理解：

优化问题的定义

这个不再理解范围内，但是，如果要用python编程进化算法的话，就需要先设置这个问题。
有单优化问题：creator.create('FitnessMin', base.Fitness, weights=(-1.0, ))

• 在创建单目标优化问题时，weights用来指示最大化和最小化。此处-1.0即代表问题是一个最小化问题，对于最大化，应将weights改为正数，如1.0。
• 另外即使是单目标优化，weights也需要是一个tuple，以保证单目标和多目标优化时数据结构的统一。
• 对于单目标优化问题，weights 的绝对值没有意义，只要符号选择正确即可。

和多优化问题:creator.create('FitnessMulti', base.Fitness, weights=(-1.0, 1.0))

• 对于多目标优化问题，weights用来指示多个优化目标之间的相对重要程度以及最大化最小化。如示例中给出的(-1.0, 1.0)代表对第一个目标函数取最小值，对第二个目标函数取最大值。

个体编码

• 实数编码(Value encoding)：直接用实数对变量进行编码。优点是不用解码，基因表达非常简洁，而且能对应连续区间。但是实数编码后搜索区间连续，因此容易陷入局部最优。
• 二进制编码(Binary encoding)：在二进制编码中，用01两种数字模拟人类染色体中的4中碱基，用一定长度的01字符串来描述变量。其优点在于种群多样性大，但是需要解码，而且不连续，容易产生Hamming cliff（例如0111=7, 1000=8，改动了全部的4位数字之后，实际值只变动了1），在接近局部最优位置时，染色体稍有变动，就会使变量产生很大偏移（格雷编码（Gray coding）能够克服汉明距离的问题，但是实际问题复杂度较大时，格雷编码很难精确描述问题）。
  
• 序列编码(Permutation encoding)：通常在求解顺序问题时用到，例如TSP问题。序列编码中的每个染色体都是一个序列。
• 粒子(Particles)：粒子是一种特殊个体，主要用于粒子群算法。相比普通的个体，它额外具有速度、速度限制并且能记录最优位置。

初始族群的创建

• 一般族群：这是最常用的族群类型，族群中没有特别的顺序或者子族群。
  toolbox.register('population', tools.initRepeat, list, toolbox.individual)
• 同类群(Demes)：同类群即一个族群中包含几个子族群。在有些算法中，会使用本地选择(Local selection)挑选育种个体，这种情况下个体仅与同一邻域的个体相互作用。

toolbox.register("deme", tools.initRepeat, list, toolbox.individual)

DEME_SIZES = 10, 50, 100
population = [toolbox.deme(n=i) for i in DEME_SIZES]

• 粒子群：粒子群中的所有粒子共享全局最优。在实现时需要额外传入全局最优位置与全局最优适应度给族群。

creator.create("Swarm", list, gbest=None, gbestfit=creator.FitnessMax)
toolbox.register("swarm", tools.initRepeat, creator.Swarm, toolbox.particle)

评价

评价部分是根据任务的特性高度定制的，DEAP库中并没有预置的评价函数模版。
这里给一个例子

from deap import base, creator, tools
import numpy as np
# 定义问题
creator.create('FitnessMin', base.Fitness, weights=(-1.0,)) #优化目标：单变量，求最小值
creator.create('Individual', list, fitness = creator.FitnessMin) #创建Individual类，继承list

# 生成个体
IND_SIZE = 5
toolbox = base.Toolbox()
toolbox.register('Attr_float', np.random.rand)
toolbox.register('Individual', tools.initRepeat, creator.Individual, toolbox.Attr_float, n=IND_SIZE)

# 生成初始族群
N_POP = 10
toolbox.register('Population', tools.initRepeat, list, toolbox.Individual)
pop = toolbox.Population(n = N_POP)

# 定义评价函数
def evaluate(individual):
  return sum(individual), #注意这个逗号，即使是单变量优化问题，也需要返回tuple

# 评价初始族群
toolbox.register('Evaluate', evaluate)
fitnesses = map(toolbox.Evaluate, pop)
for ind, fit in zip(pop, fitnesses):
  ind.fitness.values = fit
  print(ind.fitness.values)

# 结果：
# (2.593989197511478,)
# (1.1287944225903104,)
# (2.6030877077096717,)
# (3.304964061515382,)
# (2.534627558467466,)
# (2.4697149450205536,)
# (2.344837782191844,)
# (1.8959030773060852,)
# (2.5192475334239,)
# (3.5069764929866585,)

配种选择

锦标赛

deap.tools.selTournament(individuals, k, tournsize, fit_attr = 'fitness')

锦标赛选择顾名思义，就是模拟锦标赛的方式，首先在族群中随机抽取tournsize个个体，然后从中选取具有最佳适应度的个体，将此过程重复k次，获得育种族群。tournsize越大，选择强度(selection intensity)越高，在选择之后留下的育种族群的平均适应度也就越高。比较常用的tournsize是2。
假设tournsize是2，就是在原来的种群中取出来2个，然后再这两个中选一个最适应的，然后重复k次，我们就可以得到k个最适应的，这个就是育种族群，用来后面生孩子重组基因的；

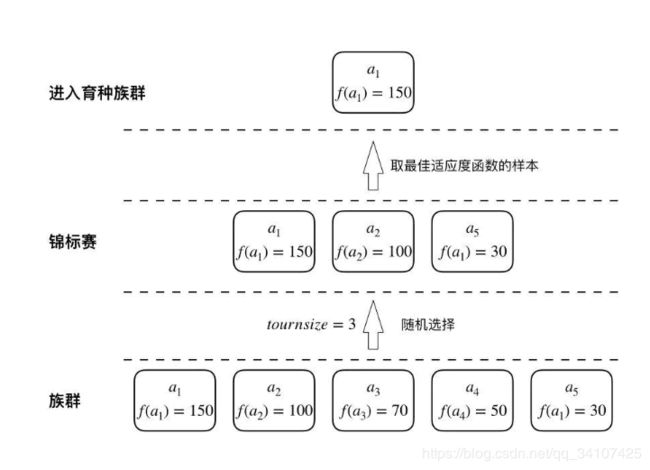
如图，假设这个族群有5个人，tournsize为3，就是选出来3个人，然后在3个人中选取一个最好的
锦标赛选择相比于轮盘赌选择，通常能够有更快的收敛速度，在实际场景中应用较多。

轮盘赌选择

deap.tools.selRoulette(individuals, k, fit_attr = 'fitness')
在轮盘赌选择中，每个个体a被选中的概率P(a)与他的评价函数f(a)成正比

\[P(a_i) = \frac{f(a_i)}{\sum_j f(a_j)} \]

但是如果评价函数出现负数，就不适用
并且很多文章指出来，轮盘赌选择的效果并不好

随机普遍抽样选择

deap.tools.selStochasticUniversalSampling(individuals, k, fit_attr = 'fitness')
随机普遍抽样选择是一种有多个指针的轮盘赌选择，其优点是能够保存族群多样性，而不会像轮盘赌一样，有较大几率对重复选择最优个体。

在与前文相同的例子中使用随机普遍抽样选择，设定指针数k为3，那么指针间距即为，如下图所示：

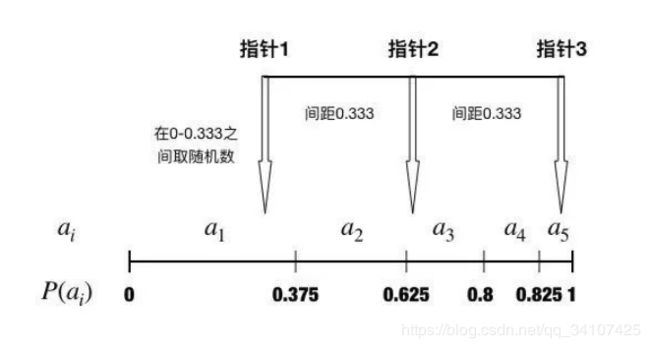
就是我一选就选3个个体，一选选3个，保证了多样性

变异

单点交叉

deap.tools.cxOnePoint(ind1, ind2)

• 最简单的交叉方式，选择一个切口，将两条基因切开之后，交换尾部基因段。尽管该方法非常简单，但是多篇文章指出，该算法在各种实验中性能都被其他交叉算法吊打，因此算是一种不建议使用的loser algorithm
  

两点交叉

deap.tools.cxTwoPoint(ind1, ind2)

• 用两个点切开基因之后，交换切出来的基因段
  

均匀交叉

deap.tools.cxUniform(ind1, ind2, indpb)

• 指定一个变异几率，两父代中的每个基因都以该几率交叉。
  

部分匹配交叉

deap.tools.cxPartialyMatched(ind1, ind2)

• 部分匹配交叉主要用于序列编码的个体
• 这个太难叙述了，能看懂就看，看不懂就记住在哪里用就好了，就是上面那句话
  

突变

高斯突变

tools.mutGaussian(individual, mu, sigma, indpb)

• 对个体序列中的每一个基因按概率变异，变异后的值为按均值为mu，方差为sigma的高斯分布选取的一个随机数。如果不希望均值发生变化，则应该将设mu为0。

乱序突变

tools.mutShuffleIndexes(individual, indpb)

• 将个体序列打乱顺序，每个基因位置变动的几率由indpb给出。

位翻转突变

tools.mutFlipBit(individual, indpb)

对个体中的每一个基因按给定对变异概率取非。

均匀整数突变

tools.mutUniformInt(individual, low, up, indpb)
对序列中的每一位按概率变异，变异后的值为[low, up]中按均匀分布随机选取的一个整数。

环境选择

完全重插入(Pure reinsertion)

• 产生与父代个体数量相当的配种个体，直接用配种个体生成新一代族群。

均匀重插入(Uniform reinsertion)

• 产生比父代个体少的配种个体，用配种个体随机均匀地替换父代个体。

精英重插入(Elitist reinsertion)

• 产生比父代个体少的配种个体，选取配种后代中适应度最好的一些个体，插入父代中，取代适应度较低的父代个体。

精英保留重插入(Fitness-based reinsertion)

• 产生比父代个体多的配种个体，选取其中适应度最大的配种个体形成新一代族群。
  通常来说后两种方式由于精英保留的缘故，收敛速度较快，因此比较推荐。

进化算法的python实现

GEAP 遗传算法/遗传编程 genetic programming + python(deap库)实现

进化算法的优缺点

优点

• 泛用性强，对连续变量和离散变量都能适用；

• 不需要导数信息，因此不要求适应度函数的连续和可微性质(或者说不需要问题内在机理的相关信息)；

• 可以在解空间内大范围并行搜索；

• 不容易陷入局部最优；

• 高度并行化，并且容易与其他优化方法整合。

• 对于凸优化问题，相对基于梯度的优化方法（例如梯度下降法，牛顿/拟牛顿法）收敛速度更慢；

• 进化算法需要在搜索空间投放大量个体来搜索最优解。对于高维问题，由于搜索空间随维度指数级膨胀，需要投放的个体数也大幅增长，会导致收敛速度变慢；

• 设计编码方式、适应度函数以及变异规则需要大量经验。
  简单说最大的缺点就是慢

参考：
GEAP 遗传算法/遗传编程 genetic programming + python(deap库)实现
【遗传编程/基因规划】Genetic Programming