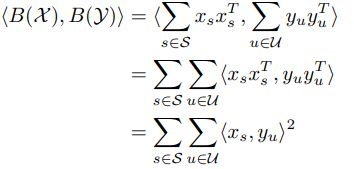多模态融合算法——Multimodal Compact Bilinear Pooling

【摘要】 很多多模态任务，都需要融合两个模态的特征。特征融合即输入两个模态的特征向量，输出融合后的向量。最常用的方法是拼接（concatenation）、按位乘（element-wise product）、按位加（element-wise sum）。MCB的作者认为这些简单的操作效果不如外积（outer product），不足以建模两个模态间的复杂关系。但外积计算存在复杂度过高的问题。

Multimodal Compact Bilinear Pooling (MCB)来自EMNLP 2016的论文《Multimodal Compact Bilinear Pooling for Visual Question Answering and Visual Grounding》。

很多多模态任务，比如VQA、视觉定位等，都需要融合两个模态的特征。特征融合即输入两个模态的特征向量，输出融合后的向量。最常用的方法是拼接（concatenation）、按位乘（element-wise product）、按位加（element-wise sum）。MCB的作者认为这些简单的操作效果不如外积（outer product），不足以建模两个模态间的复杂关系。但外积计算存在复杂度过高的问题。n维的向量，外积计算得到n^2的向量。于是MCB被提出，MCB将外积的结果映射到低维空间中，并且不需要显式计算外积。

MCB

双线性（Bilinear）就是向量外积的计算。双线性池化（Bilinear Pooling）是对双线性融合后的特征进行池化。在[2]中，双线性池化首先对卷积得到的feature map的每个位置的特征向量进行向量外积计算，再对所有位置外积计算的结果进行sum pooling得到特征向量x。x经过signed square root和L2 normalization得到最后的特征。

但是双线性特征的维度是极高的，Compact Bilinear Pooling（CBP）[3]是对双线性池化的一种降低维度的近似。

双线性池化的操作可以表示为：

在线性核的情况下有：

因为：

对多项式核的进行低维近似的映射函数Φ，可以用来做对双线性池化的压缩。Tensor Sketching [4]是一种近似多项式核的算法，可以用Tensor Sketching进行压缩。使用Tensor Sketching进行近似双线性池化的算法如下：

其中Count Sketch function有良好的性质：

MCB对CBP进行改进，使其适用于融合不同模态的特征。MCB的计算方法如Figure2所示。

首先两个模态的特征向量分别通过Count Sketch映射函数得到特征的Count Sketch。再经过FFT和逆FFT得到融合的特征。

具体的计算步骤如Algorithm1所示。

VQA

将MCB应用于VQA的框图如下：

这里用到了两次MCB模块，第一个MCB融合图像特征和文本特征计算图像每个空间位置的attention weight。第二个MCB融合图像特征和文本特征得到答案。

下面是在VQA数据集上使用不同融合方式的实验结果。

Visual Grounding

Visual Grounding的框图如下：

MCB将图像proposal的特征和问题的文本特征融合。

下面是在Flickr30k实体数据集上的结果。

参考资料

[1] Fukui A, Park D H, Yang D, et al. Multimodal compact bilinear pooling for visual question answering and visual grounding[J]. arXiv preprint arXiv:1606.01847, 2016.

[2] Lin T Y, RoyChowdhury A, Maji S. Bilinear cnn models for fine-grained visual recognition[C]//Proceedings of the IEEE international conference on computer vision. 2015: 1449-1457.

[3] Gao Y, Beijbom O, Zhang N, et al. Compact bilinear pooling[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2016: 317-326.

[4] Pham N, Pagh R. Fast and scalable polynomial kernels via explicit feature maps[C]//Proceedings of the 19th ACM SIGKDD international conference on Knowledge discovery and data mining. 2013: 239-247.

[5] https://zhuanlan.zhihu.com/p/62532887

作者：冰糖柠萌