新型冠状病毒传染模型SI、SIS、SIR、SEIR
SI模型
在经典的传染病模型中,种群(Population)内N个个体的状态可分为如下几类:
**易感状态(Susceptible):**一个个体在感染前是处于易感状态的,即该个体有可能被邻居个体感染。
**感染状态I(Infected):**一个感染上某种病毒的个体就称为是处于感染状态。,即该个体还会以一定概率感染其邻居个体。
**移除状态(Remove,Refractory或者Recovered):**也成为免疫状态或恢复状态,当一个个体经历过一个完整的感染周期后,该个体就不再被感染,因此就可以不再考虑改革提。
SI传播模型是最简单的疾病传播模型,模型中的所有个体都只可能处于两个状态中的一个:即易感(S)状态或感染(I)状态。
SI模型中的个体一旦被感染后就永远处于感染状态。
在给定时刻t,令S(t)与I(t)分别代表该时刻处于易感和感染状态的个体数目,显然有
S(t)+I(t)恒等于N,这里,N是个体总数。随着时间t的增长,易感个体与感染个体的接触会导致感染个体数量的增加。加入由于个体之间的接触而导致疾病传播的概率为β,疾病仅在感染个体和易感个体之间进行接触时才会以概率β将疾病传染给易感个体。在时刻t,易感个体的比例为S(t)/N,感染个体的数量为I(t),一次,易感个体的数量将以如下变化率减少
ds/dt = -β*S(t)I(t)/N
同时,感染个体的数量会以与易感个体相反的变化率增加,
ds/dt = βS(t)*I(t)/N
分别将时刻t处于易感状态和感染状态的个体所占比例记为,
s(t)=S(t)/N
i(t)=I(t)/N
显然有,
s(t)+i(t)恒等于1,此时之前的公式可以记做
ds/dt=-βsi
di/dt=βsi
即 di/dt=βi(1-i)
```python
def diff_eqs1(INP,t):
Y=np.zeros((2))
V = INP
Y[0] = - beta * V[0] * V[1] + gamma * V[1]
Y[1] = beta * V[0] * V[1] - gamma * V[1]
return Y
t_start = 0.0
t_end = ND
t_inc = TS
t_range = np.arange(t_start, t_end+t_inc, t_inc) #生成日期范围
RES = spi.odeint(diff_eqs1,INPUT,t_range)
pl.plot(RES[:,0], 'b', label='易感者')
pl.plot(RES[:,1], 'r', label='传染者')
pl.legend(loc=0)
pl.title('SI-nCoV 传播时间曲线')
pl.xlabel('时间(天)')
pl.ylabel('人数比例')
pl.savefig('SI-nCoV 传播时间曲线.png', dpi=900)
pl.show()
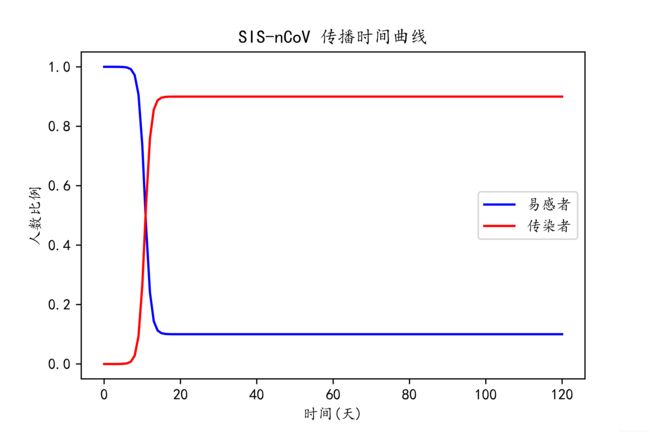
SIS模型
在SI模型基础上加入康复的概率,即治愈率
S:易感者
I:感染者
a:感染率
b:治愈率
条件:
1、在疾病传播期间总人数N不变, N=S+I
2、每个病人每天接触人数为定值
3、病人每天治愈率定值
```python
beta=1.4247
gamma=0.14286
I0=1e-6
ND=70
TS=1.0
INPUT = (1.0-I0, I0)
def diff_eqs2(INP,t):
Y=np.zeros((2))
V = INP
Y[0] = - beta * V[0] * V[1] + gamma * V[1]
Y[1] = beta * V[0] * V[1] - gamma * V[1]
return Y
t_range = np.arange(t_start, t_end+t_inc, t_inc)
RES = spi.odeint(diff_eqs2,INPUT,t_range)
pl.plot(RES[:,0], '-b', label='易感者')
pl.plot(RES[:,1], '-r', label='传染者')
pl.legend(loc=0)
pl.title('SIS-nCoV 传播时间曲线')
pl.xlabel('时间(天)')
pl.ylabel('人数比例')
pl.savefig('SIS-nCoV 传播时间曲线.png', dpi=900) # This does increase the resolution.
pl.show()
SIR模型
alpha=0.000004
beta= 0.1
TS=1.0 #观察间隔
ND=120.0 #观察结束日期
S0=100000 #初始易感人数
I0=10 #初始感染人数
INPUT = (S0, I0, 0.0)
def diff_eqs(INP,t):
Y=np.zeros((3))
V = INP
Y[0] = - alpha * V[0] * V[1]
Y[1] = alpha * V[0] * V[1] - beta * V[1]
Y[2] = beta * V[1]
return Y
t_start = 0.0
t_end = ND
t_inc = TS
t_range = np.arange(t_start, t_end+t_inc, t_inc) #生成日期范围
RES = spi.odeint(diff_eqs,INPUT,t_range)
pl.plot(RES[:,0], '-g', label='易感者')
pl.plot(RES[:,1], '-r', label='传染者')
pl.plot(RES[:,2], '-k', label='移除者')
pl.legend(loc=0)
pl.title('SIR-nCoV 传播时间曲线')
pl.xlabel('时间(天)')
pl.ylabel('人数')
pl.savefig('SIR-nCoV 传播时间曲线.png', dpi=900)
pl.show()
SEIR模型
引入潜伏者
S:易感者 a:接触率
E:潜伏者 b:感染率
I:感染者 i: 转病率
R:康复者 r:治愈率
D:死亡者 k:病死率
微分方程为:


def calc(T):
for i in range(0, len(T) - 1):
S.append(S[i] - r * b * S[i] * I[i] / N - r2 * b2 * S[i] * E[i] / N)
E.append(E[i] + r * b * S[i] * I[i] / N - a * E[i] + r2 * b2 * S[i] * E[i] / N)
I.append(I[i] + a * E[i] - y * I[i])
R.append(R[i] + y * I[i])
全部python文件为:
```python
import math
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import scipy.integrate as spi
import pylab as pl
plt.rcParams['font.sans-serif'] = ['KaiTi']
plt.rcParams['axes.unicode_minus'] = False
def calc(T):
for i in range(0, len(T) - 1):
S.append(S[i] - r * b * S[i] * I[i] / N - r2 * b2 * S[i] * E[i] / N)
E.append(E[i] + r * b * S[i] * I[i] / N - a * E[i] + r2 * b2 * S[i] * E[i] / N)
I.append(I[i] + a * E[i] - y * I[i])
R.append(R[i] + y * I[i])
beta=1.4247
gamma=0
I0=1e-6
INPUT = (1.0-I0, I0)
def diff_eqs1(INP,t):
Y=np.zeros((2))
V = INP
Y[0] = - beta * V[0] * V[1] + gamma * V[1]
Y[1] = beta * V[0] * V[1] - gamma * V[1]
return Y
t_start = 0.0
t_end = ND
t_inc = TS
t_range = np.arange(t_start, t_end+t_inc, t_inc) #生成日期范围
RES = spi.odeint(diff_eqs1,INPUT,t_range)
pl.plot(RES[:,0], 'b', label='易感者')
pl.plot(RES[:,1], 'r', label='传染者')
pl.legend(loc=0)
pl.title('SI-nCoV 传播时间曲线')
pl.xlabel('时间(天)')
pl.ylabel('人数比例')
pl.savefig('SI-nCoV 传播时间曲线.png', dpi=900)
pl.show()
beta=1.4247
gamma=0.14286
I0=1e-6
ND=70
TS=1.0
INPUT = (1.0-I0, I0)
def diff_eqs2(INP,t):
Y=np.zeros((2))
V = INP
Y[0] = - beta * V[0] * V[1] + gamma * V[1]
Y[1] = beta * V[0] * V[1] - gamma * V[1]
return Y
t_range = np.arange(t_start, t_end+t_inc, t_inc)
RES = spi.odeint(diff_eqs2,INPUT,t_range)
pl.plot(RES[:,0], '-b', label='易感者')
pl.plot(RES[:,1], '-r', label='传染者')
pl.legend(loc=0)
pl.title('SIS-nCoV 传播时间曲线')
pl.xlabel('时间(天)')
pl.ylabel('人数比例')
pl.savefig('SIS-nCoV 传播时间曲线.png', dpi=900) # This does increase the resolution.
pl.show()
alpha=0.000004
beta= 0.1
TS=1.0 #观察间隔
ND=120.0 #观察结束日期
S0=100000 #初始易感人数
I0=10 #初始感染人数
INPUT = (S0, I0, 0.0)
def diff_eqs(INP,t):
Y=np.zeros((3))
V = INP
Y[0] = - alpha * V[0] * V[1]
Y[1] = alpha * V[0] * V[1] - beta * V[1]
Y[2] = beta * V[1]
return Y
t_start = 0.0
t_end = ND
t_inc = TS
t_range = np.arange(t_start, t_end+t_inc, t_inc) #生成日期范围
RES = spi.odeint(diff_eqs,INPUT,t_range)
pl.plot(RES[:,0], '-g', label='易感者')
pl.plot(RES[:,1], '-r', label='传染者')
pl.plot(RES[:,2], '-k', label='移除者')
pl.legend(loc=0)
pl.title('SIR-nCoV 传播时间曲线')
pl.xlabel('时间(天)')
pl.ylabel('人数')
pl.savefig('SIR-nCoV 传播时间曲线.png', dpi=900)
pl.show()
def plot(T,S,E,I,R):
plt.figure()
plt.title("SEIR-nCoV 传播时间曲线")
plt.plot(T,S,color='r',label='易感者')
plt.plot(T, E, color='k', label='潜伏者')
plt.plot(T, I, color='b', label='传染者')
plt.plot(T, R, color='g', label='移除者')
plt.grid(False)
plt.legend()
plt.xlabel("时间(天)")
plt.ylabel("人数")
pl.savefig('SEIR-nCoV 传播时间曲线.png', dpi=900)
plt.show()
if __name__ == '__main__':
N = 100000 # 人口总数
E = [] # 潜伏携带者
E.append(0)
I = [] # 传染者
I.append(1)
S = [] # 易感者
S.append(N - I[0])
R = [] # 康复者
R.append(0)
r = 20 # 传染者接触人数
b = 0.03 # 传染者传染概率
a = 0.1 # 潜伏者患病概率
r2 = 30 # 潜伏者接触人数
b2 = 0.03 # 潜伏者传染概率
y = 0.1 # 康复概率
T = [i for i in range(0, 120)] # 时间
calc(T)
plot(T,S,E,I,R)
改进SEIR1
结合现实:
1、武汉疫情12月30日发现第一例疫情患者,1月23日开始封城,第25天时对应减少模型的病者的日接触人数,作为采取隔离措施的体现。
2、将潜伏者与患病者的转染易感者的概率与日接触人数分开为两个参数。



改进SEIR模型2
1.引入潜伏者转阴率
2.武汉医院增多,康复率增加
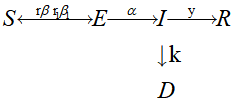

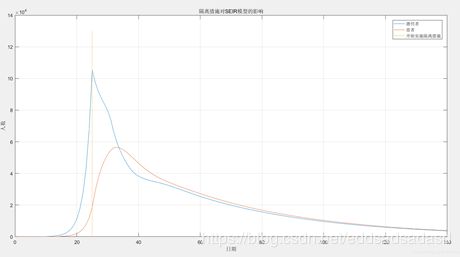
接触过患者的潜伏者明显下降,在之后的约半个月后疫情到达拐点,患病人数峰值约为6万,随后疫情得到控制。




