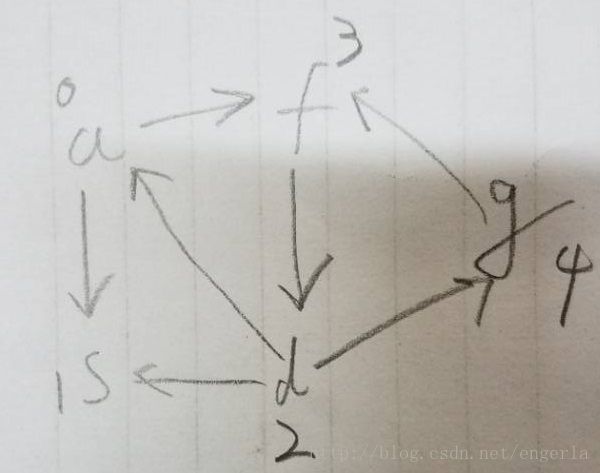
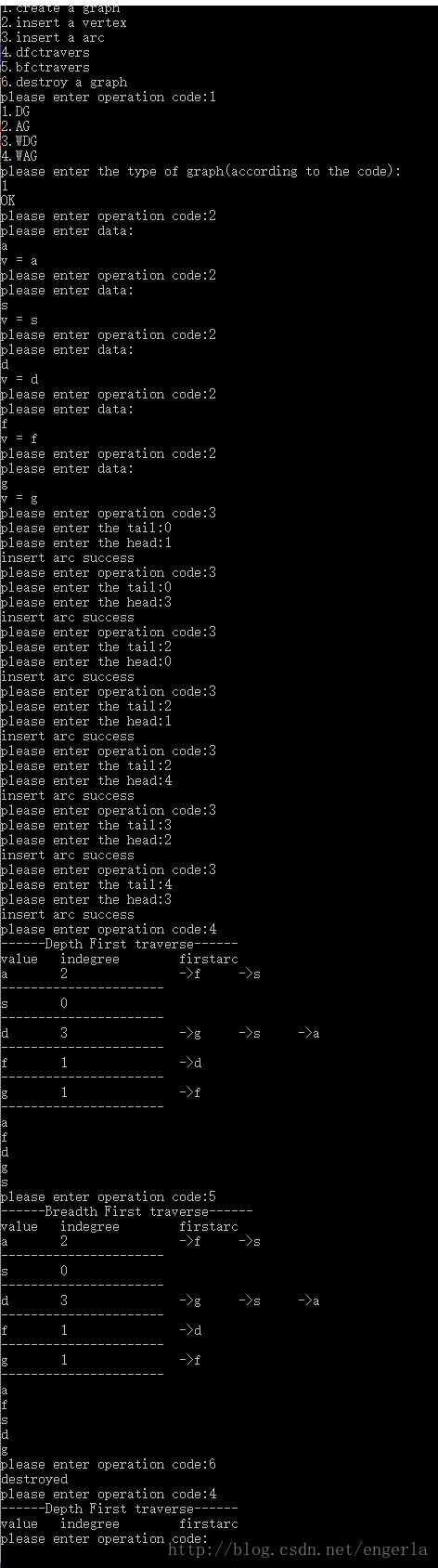
图的邻接表存储及基本操作

图的存储方式有很多种，这里是以邻接表存储为例实现的。图的基本操作包括初始化一个空图、插入一节点、插入条边、深度优先遍历、广度优先遍历、销毁图等

#include
#include
#define OK 1
#define ERROR -1
#define MAX_VEX 10//最大顶点数
typedef int InfoType;
typedef char VexType;//顶点的类型
typedef int WeightType;//权值的类型

图的种类（有向图、无向图、加权有向图、加权无向图），采用枚举法

typedef enum
{
	DG = 1, AG, WDG, WAG//有向图  无向图  带权有向图  带权无向图
}GraphKind;

邻接表的前半部分是顺序表，所以定义一个顺序表的结构体

typedef struct VexNode
{
	VexType data;//顶点的值
	int indegree;//顶点的度
	LinkNode *firstarc;//指向第一个表节点，有向图是入度或出度或没有
}VexNode;//顶点节点类型定义

邻接表后半部分是链表，所以定一个链表的结构体

typedef struct LinkNode
{
	int adjvex;//邻接点在头结点数组中的位置（下标）
	InfoType info;//节点信息   如权值
	struct LinkNode *nextarc;//指向下一个表节点
}LinkNode;

接下来定义图的结构体

typedef struct
{
	GraphKind kind;
	int vexnum;//顶点的个数
	VexNode AdjList[MAX_VEX];//头结点的类型的数组
}ALGraph;

在图的一系列基本操作中需要队列的帮助

//队列的结构体
typedef struct SqQueue
{
	VexType array[MAX_VEX];
	int front;
	int rear;
}SqQueue;


//初始化一个空队列
SqQueue Creat_SqQueue()
{
	SqQueue Q;
	Q.front = 0;
	Q.rear = 0;
	return Q;
}

//入队列  若成功返回1  否则返回-1
int InsertQueue(SqQueue *Q, VexType e)
{
	if ((Q->rear+1)%MAX_VEX == Q->front)
	{
		printf("The queue is full.\n");
		return ERROR;
	}
	else
	{
		Q->array[Q->rear] = e;
		Q->rear = (Q->rear + 1) % MAX_VEX;
		//printf("Insert success!\n\n");
	}
	return OK;
}

//出队列 若成功返回弹出的元素  若不成功返回-1
VexType DeletaQueue(SqQueue *Q)
{
	VexType e = 0;
	if (Q->front == Q->rear)
	{
		printf("This queue is empty!\n");
		return ERROR;
	}
	else
	{
		e = Q->array[Q->front];
		Q->front = (Q->front + 1) % MAX_VEX;
		//printf("Delete success!\n");
	}
	return e;
}

建立一个空图

ALGraph CreatGraph() {
	ALGraph G;
	int i;//循环变量
	int a = 0;
	printf("1.DG\n2.AG\n3.WDG\n4.WAG\n");
	printf("please enter the type of graph(according to the code):\n");
	scanf("%d", &a);//确定图的类型
	switch (a)
	{
	case 1:
		G.kind = DG;
		break;
	case 2:
		G.kind = AG;
		break;
	case 3:
		G.kind = WDG;
		break;
	case 4:
		G.kind = WAG;
		break;
	default:
		printf("The type of the graph is error\n");
		break;
	}
	G.vexnum = 0;//结点个数置为0
	for (i = 0; i < MAX_VEX; i++)//把所有节点的度置为0
	{
		G.AdjList[i].indegree = 0;
		G.AdjList[i].firstarc = NULL;
	}
	return G;
}

插入节点时需要判断节点是否在，若不存在插入，如存在插入失败

//定位节点  若存在返回1  若不存在返回-1
int LocateVex(ALGraph *G, VexType v) {
	int i = 0;
	int a = 0;
	printf("v = %c\n", v);
	for (i = 0; i < G->vexnum; i++)
	{
		if (G->AdjList[i].data == v)
		{
			a++;
			break;
		}
	}
	if (a == 0)
	{
		return ERROR;
	}
	return OK;
}

在图中插入一个节点

void InsertVex(ALGraph *G){
	int res = 0;
	if (G->vexnum + 1 == MAX_VEX)
	{
		printf("The graph is overflow!\n");
	}
	else
	{
		VexType u = '\0';
		printf("please enter data:\n");
		getchar();
		scanf("%c", &u);
		res = LocateVex(G, u);
		if (res == -1)//没有节点   添加
		{
			G->AdjList[G->vexnum].data = u;
			G->AdjList[G->vexnum].firstarc = NULL;
			G->vexnum++;
			//printf("insert vertex success\n");
		}
		else
		{
			printf("insert vertex fail\n");
		}
	}
}

在图中插入一条边时，要判断图的类型，不同的类型，插入操作是不一样的

void InsertArc(ALGraph *G) {
	if (G->kind == DG)//有向图
	{
		LinkNode *p;
		LinkNode *r;
		int tail = 0;//弧尾（起点）
		int head = 0;//弧头（终点）
		p = (LinkNode *)malloc(sizeof(LinkNode));
		printf("please enter the tail:");
		scanf("%d", &tail);
		printf("please enter the head:");
		scanf("%d", &head);
		if (tail < G->vexnum && head < G->vexnum)
		{
			p->adjvex = head;
			p->nextarc = NULL;
			p->info = 0;
			r = G->AdjList[tail].firstarc;
			p->nextarc = r;
			G->AdjList[tail].firstarc = p;
			G->AdjList[tail].indegree++;
			printf("insert arc success\n");
		}
		else
		{
			printf("vertex is not exit.");
		}
	}
	else if(G->kind == AG)//无向图
	{
		LinkNode *p;
		LinkNode *q;
		LinkNode *r;
		LinkNode *s;
		int tail = 0;
		int head = 0;
		p = (LinkNode *)malloc(sizeof(LinkNode));
		q = (LinkNode *)malloc(sizeof(LinkNode));
		s = (LinkNode *)malloc(sizeof(LinkNode));
		printf("please enter the tail:");
		scanf("%d", &tail);
		printf("please enter the head:");
		scanf("%d", &head);
		if (tail < G->vexnum && head < G->vexnum)
		{
			p->adjvex = head;
			p->info = 0;
			p->nextarc = NULL;
			r = G->AdjList[tail].firstarc;
			p->nextarc = r;
			G->AdjList[tail].firstarc = p;

			s->adjvex = tail;
			s->info = 0;
			q = G->AdjList[head].firstarc;
			s->nextarc = q;
			G->AdjList[head].firstarc = s;

			G->AdjList[tail].indegree++;
			G->AdjList[head].indegree++;
			printf("insert arc success\n");
		}
		else
		{
			printf("vertex is not exit.\n");
		}

	}
	else if (G->kind == WDG)//加权有向图
	{
		LinkNode *p;
		LinkNode *r;
		int info = 0;
		int tail = 0;//弧尾（起点）
		int head = 0;//弧头（终点）
		p = (LinkNode *)malloc(sizeof(LinkNode));
		printf("please enter the tail:");
		scanf("%d", &tail);
		printf("please enter the head:");
		scanf("%d", &head);
		printf("please enter the information:");
		scanf("%d", &info);
		if (tail < G->vexnum && head < G->vexnum)
		{
			p->adjvex = head;
			p->nextarc = NULL;
			p->info = info;
			r = G->AdjList[tail].firstarc;
			p->nextarc = r;
			G->AdjList[tail].firstarc = p;
			G->AdjList[tail].indegree++;
			printf("insert arc success\n");
		}
		else
		{
			printf("vertex is not exit.\n");
		}

	}
	else if(G->kind == WAG)//加权无向图
	{
		LinkNode *p;
		LinkNode *q;
		LinkNode *r;
		LinkNode *s;
		int info = 0;
		int tail = 0;
		int head = 0;
		p = (LinkNode *)malloc(sizeof(LinkNode));
		q = (LinkNode *)malloc(sizeof(LinkNode));
		s = (LinkNode *)malloc(sizeof(LinkNode));
		printf("please enter the tail:");
		scanf("%d", &tail);
		printf("please enter the head:");
		scanf("%d", &head);
		printf("please enter the information:");
		scanf("%d", &info);
		if (tail < G->vexnum && head < G->vexnum)
		{
			p->adjvex = head;
			p->nextarc = NULL;
			p->info = info;
			r = G->AdjList[tail].firstarc;
			p->nextarc = r;
			G->AdjList[tail].firstarc = p;

			s->adjvex = tail;
			s->info = info;
			q = G->AdjList[head].firstarc;
			s->nextarc = q;
			G->AdjList[head].firstarc = s;

			G->AdjList[tail].indegree++;
			G->AdjList[head].indegree++;
			printf("insert arc success\n");
		}
		else
		{
			printf("vertex is not exit.\n");
		}
	}
	else
	{
		printf("The type of the graph is error\n");
	}
}

图的深度优先遍历

void DFSTraverse(ALGraph *G, int v, int visit[]) {
	LinkNode *p;

	if (visit[v] == 0)
	{
		printf("%c\n", G->AdjList[v].data);
		visit[v] = 1;
		p = G->AdjList[v].firstarc;

		while (p != NULL)
		{
			if (visit[p->adjvex] == 0)
			{
				DFSTraverse(G, p->adjvex, visit);
			}
			p = p->nextarc;
		}
	}
}

图的广度优先遍历

void BFSTraverse(ALGraph *G){
    int i = 0;//循环变量
    int k = 0;//循环变量
	SqQueue Q = Creat_SqQueue();
	//visited为访问标志数组，为0则该节点没被访问过，为1则被访问过
	int visited[MAX_VEX];
	LinkNode *p;
	for (i = 0; i < MAX_VEX; i++)//访问标志初始化
	{
		visited[i] = 0;
	}
	//广度优先遍历图
	for (k = 0; k < G->vexnum; k++)
	{
		if (visited[k] == 0)//若该节点没有被访问过
		{
			InsertQueue(&Q, k);
			visited[k] = 1;
			if (G->AdjList[k].firstarc != NULL)
			{
				p = G->AdjList[k].firstarc;
				while (p != NULL)
				{
				    if(visited[p->adjvex] == 0)
                    {
                        InsertQueue(&Q, p->adjvex);
                        visited[p->adjvex] = 1;
                    }
					p = p->nextarc;
				}
			}
		}
		else//若该节点被访问过
        {
            if (G->AdjList[k].firstarc != NULL)
			{
				p = G->AdjList[k].firstarc;
				while (p != NULL)
				{
				    if(visited[p->adjvex] == 0)
                    {
                        InsertQueue(&Q, p->adjvex);
                        visited[p->adjvex] = 1;
                    }
					p = p->nextarc;
				}
			}
		}
	}
	while (Q.front != Q.rear)//循环弹出队列中的元素
	{
		printf("%c\n", G->AdjList[DeletaQueue(&Q)].data);
	}
}

销毁一个图

int DestroyGeaph(ALGraph *G) {
    int i = 0;//循环变量
	for (i = 0; i < G->vexnum; i++)
	{
		G->AdjList[i].data = 0;
		G->AdjList[i].indegree = 0;
		G->AdjList[i].firstarc = NULL;
	}
	G->vexnum = 0;
	return OK;
}

以邻接表的形式输出图

void OutPutGraph(ALGraph G)
{
    int i = 0;//循环变量
	printf("value\tindegree\tfirstarc\n");
	for (i = 0; i < G.vexnum; i++)
	{
		printf("%c\t", G.AdjList[i].data);
		printf("%d\t\t", G.AdjList[i].indegree);
		LinkNode *p;
		p = G.AdjList[i].firstarc;
		while (p != NULL)
		{
			printf("->");
			printf("%c \t", G.AdjList[p->adjvex].data);
			p = p->nextarc;
		}
		printf("\n");
		printf("----------------------\n");
	}
}

示例：

运行结果：

以上就是图的基本操作了，主方法就不写了，大家根据可以自己的需要写，希望大家看了以后能帮得上忙。