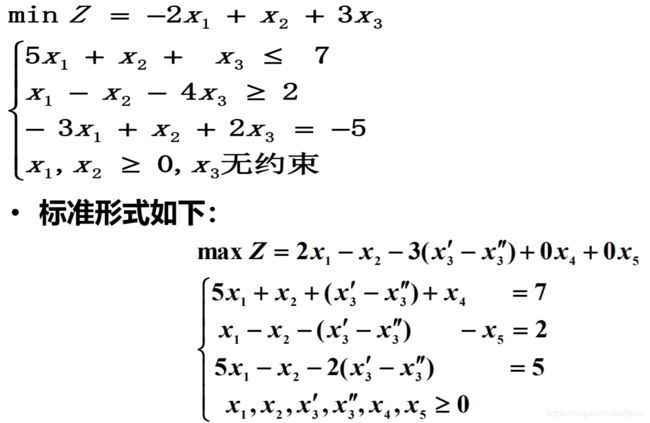【运筹与优化】单纯形法解线性规划问题(matlab实现)
文章目录
- 单纯形法步骤:
- 1.将线性规划问题化为标准形式
- 2.列出单纯形表
- 3.进行最优性检验
- 4.从一个基可行解转换到另一个目标值更大的基可行解,列出新的单纯形表
- 5.重复3、4直到计算结束为止
- 举例
- 单纯形法matlab实现
单纯形法是一种解线性规划问题的算法,其求解过程是通过构造一个单纯形表实现的,具体步骤如下:
单纯形法步骤:
1.将线性规划问题化为标准形式
标准形式如下:

其特点是:
(1) 目标函数求最大值(有时求最小值)
(2) 约束条件都为等式方程,且右端常数项 bi 都大于或等
于零
(3) 决策变量 xj 为非负
为了方便使用单纯形法来求解线性规划问题,我们需要将现有问题化为标准形式,其方法如下:
(1) 目标函数的转换

(2) 无约束变量的转换

(3) 约束方程由不等式转为等式
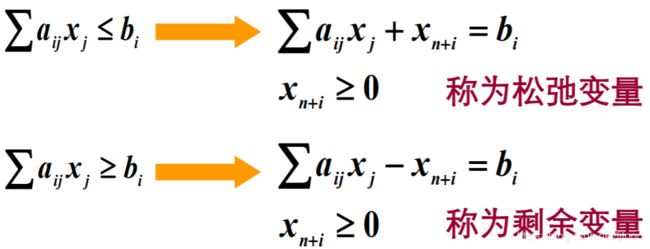
(4) 小于等于0的变量的转换
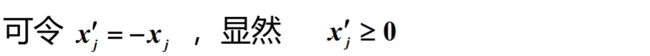
2.列出单纯形表
对于已经化为标准型的线性规划问题

其对应的单纯形表如下:

其中:

例如以下已经化为标准型的线性规划问题:
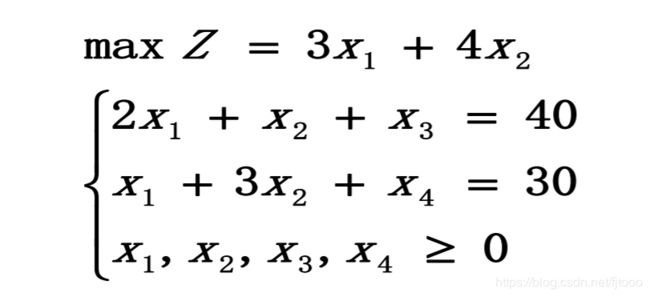
其单纯形表如下:
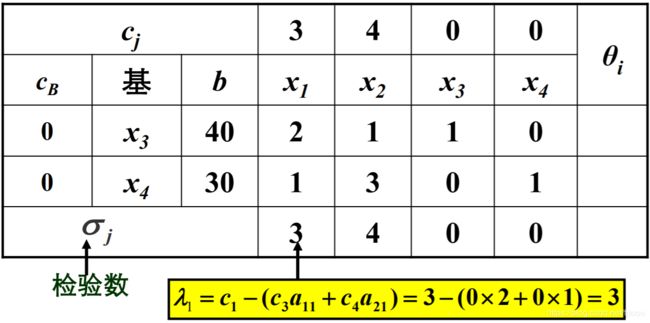
3.进行最优性检验
如果表中所有的检验数都小于等于0,则表中的基可行解就是问题的最优解,计算停止,否则进行下一步。
4.从一个基可行解转换到另一个目标值更大的基可行解,列出新的单纯形表
5.重复3、4直到计算结束为止
重复3、4步骤,直到表中所有的检验数都小于等于0,计算结束,表中的基可行解就是问题的最优解。
举例

将问题化为标准型,加入松弛变量x3,x4:
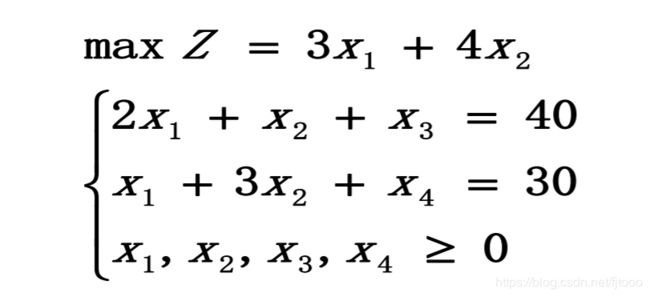
运用单纯形表求解:
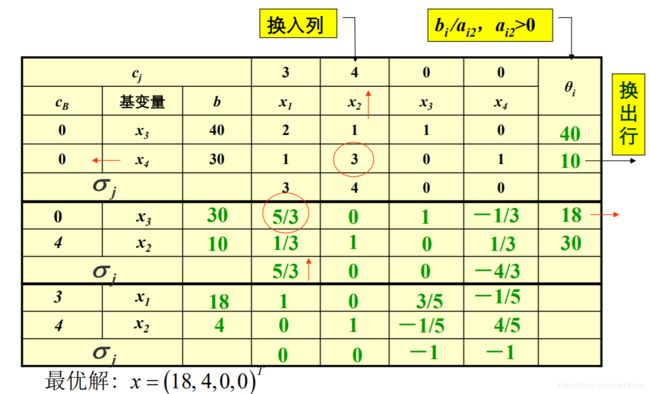
注:本次求解进行了两次迭代,上图把初始单纯形表和两次迭代时的单纯性表从上到下拼接在了一起。
单纯形法matlab实现
Simplex_eye.m:
function [x_opt, fx_opt, iter, Table] = Simplex_eye(A,b,c)
% A = [2 -3 2 1 0; 1/3 1 5 0 1];
% b = [12 20]';
% c = [1 2 1 0 0]';
%初始单纯型表
Table = zeros(size(A,1)+1, size(A,2)+1);
Table(1:size(A,1), 1:size(A,2)) = A;
Table(size(A,1)+1, 1:size(A,2)) = c';
Table(1:size(A,1), size(A,2)+1) = b;
[m, n] = size(Table); %m为行数,n为列数
base = Find_indentity(A); %调用函数,找单位矩阵的列下标
iter = 0; %迭代次数
while sum(Table(size(Table,1), 1:size(Table,2))>0)
%循环条件:当存在大于零的检验数就继续循环
iter = iter + 1;
index_col = find(Table(m,:) == max(Table(m,:))); %找最大检验数所在列
pos = find(Table(1:m-1, index_col) > 0);
temp = zeros(1,size(pos,2));
for i = 1:size(pos,1)
temp(i) = Table(pos(i), n)/Table(pos(i), index_col);
end
index_row = pos(temp == min(temp)); %找主元行
%以下做初等行变换
Table(index_row,:) = Table(index_row, :)./Table(index_row,index_col);
for i = 1:index_row-1
Table(i,:) = Table(i,:)-Table(i,index_col)*Table(index_row,:);
end
for i = index_row+1 : m
Table(i,:) = Table(i,:)-Table(i,index_col)*Table(index_row,:);
end
base(index_row) = index_col; %换基,把第index_row个基换成index_col
end
x_opt = zeros(1,size(c,2));
for i = 1:size(base, 1)
x_opt(1,base(i)) = Table(i,n);
end
fx_opt = -1*Table(size(Table,1), size(Table,2));
end
找单位矩阵列下标 Find_indentity.m:
function [index] = Find_indentity(A)
function [index] = Find_indentity(A)
[m,n] = size(A);
index = zeros(m,1);
for i = 1:m
temp = find(A(i,:)==1);
if size(temp,2) == 1
index(i,1) = temp;
else
for t = 1:size(temp,2)
flag = 0;
for r = 1:i-1
if A(r, temp(1, t)) ~= 0
flag = 1;
break;
end
end
for r = i+1:m
if A(r, temp(1, t)) ~= 0
flag = 1;
break;
end
end
if flag == 0
index(i,1) = temp(1, t);
break;
end
end
end
end
end