看数据结构写代码(56) 平衡二叉树(AVL树)
平衡二叉树的定义 (AVL—— 发明者为Adel'son-Vel'skii 和 Landis)
算法演示网址:http://www.cnblogs.com/abatei/archive/2008/11/17/1335031.html
平衡二叉查找树,又称 AVL树。 它除了具备二叉查找树的基本特征之外,还具有一个非常重要的特点:它 的左子树和右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值(平衡因子 ) 不超过1。 也就是说AVL树每个节点的平衡因子只可能是-1、0和1(左子树高度减去右子树高度)。
这样 可以 使得 在 查找,删除,插入时 的 时间 复杂度 稳定 在 O(logn) 。
那么如何是二叉查找树在添加数据的同时保持平衡呢?基本思想就是:当在二叉排序树中插入一个节点时,首先检查是否因插入而破坏了平衡,若 破坏,则找出其中的最小不平衡二叉树,在保持二叉排序树特性的情况下,调整最小不平衡子树中节点之间的关系,以达 到新的平衡。所谓最小不平衡子树 指离插入节点最近且以平衡因子的绝对值大于1的节点作为根的子树
对 最小平衡子树中节点的 调整 不会 改变 树的 高度,所以 不会 改变祖先节点的 平衡因子。
那么 如何 让 二叉树 平衡呢?
书上 已经 说了 有 四种 需要 需要 改变的 情况 ,分别 为 LL型,LR型,RR型,RL型。 如果 你没听说过,请 去 看书。
首先 向 大家 介绍 两个 基本 原型 。
LL型 和 LR 在插入之前的 原型: -----------------------------------RR型 和 RL型 插入之前的 原型:
这两个图 是 我见过的 能够 合理 解释 所有 思路的 最好的 图,其他 网上的 单支图,只能 让你 更加 迷糊。图中的 0,-1,1 代表 平衡因子。
我们从 两方面 来 看 平衡算法:
1.算法思路
2. 平衡后,平衡因子的改变
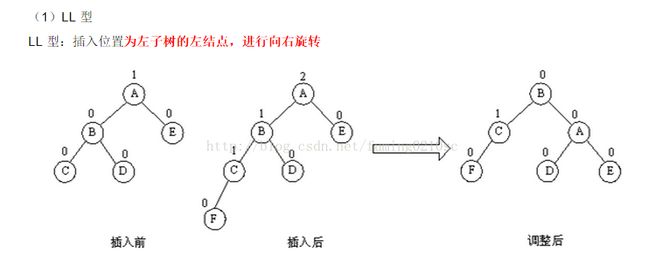
首先 说 LL型(插入在左子树的左子树), 当我们 在 节点 c上 插入 一个 节点F(插在左子树 或者 右子树上 无区别)。 这样 节点a 的平衡因子 变成 2了。
具体的思路 是更换 根节点的 思路:然后 我们 让 B 节点 成为 根节点,用 A替换 D节点,成为B节点的左子树,让 D节点 成为A节点的左子树。(或者 压入思想: 将A 结果 压到 B 节点的 右子树上,原有 B节点的 右子树变成 A的左子树)。
) 这样的操作 叫做 向右 旋转。(从图上看上去 是 把 A节点 压倒 右下 方)。
在平衡化之后,仅 有 原 根节点 A 和 现在的 根节点 B 的 平衡因子 变为 0,其余 不变。
具体代码 如下:
//右旋转,可以看成是 类似 交换两个值 的 步骤
void R_Rotate(AvlTree * tree){
AvlTree lc = (*tree)->lChild;//左孩子
(*tree)->lChild = lc->rChild;
lc->rChild = (*tree);
*tree = lc;
}
RR型:我们在 E节点 插入 一个节点F(在左 在右 无关系),导致 A节点 平衡因子 变为 -2.
具体思路: 我们 让 A节点 的 右孩子 C节点 成为 根节点,让 A 替换D 的位置, 成为 C节点 的 左孩子,让 D 成为 A 的 右孩子。从图上看 是 把 A节点 往 左下角 压了 一个层次,我们 叫做 左旋转。
在平衡化之后,仅 有 原 根节点 A 和 现在的 根节点 B 的 平衡因子 变为 0,其余 不变。
具体代码: 记忆 思路 和 右旋转一致
//左旋转
void L_Rotate(AvlTree * tree){
AvlTree rc = (*tree)->rChild;//右孩子
(*tree)->rChild = rc->lChild;
rc->lChild = *tree;
*tree = rc;//最后替换根节点
}
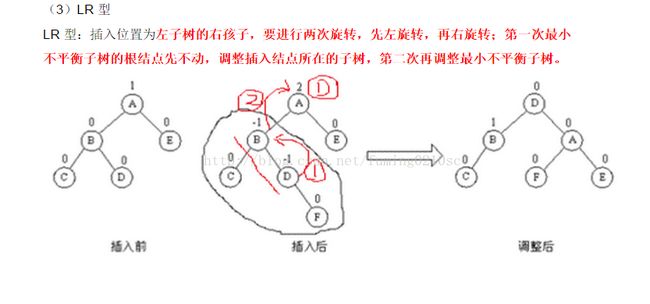
解决思路:先 将 A的左子树 B左旋,再将 A 右旋。
LRL:插入在 D节点 的 左子树上,A 平衡后 ,平衡因子 为 -1(下面的 图 有误), B平衡因子 为 0..,D的平衡因子为0
LRR:F插入在D节点 的 右子树上,A平衡因子 为0,B平衡因子 为1,最后的根节点D节点平衡因子为0.
在仔细研究之后 发现 还有 一种 是 底下 代码的 case EH 的类型,就是 上图的 只有 AB节点,然后插入 一个 D节点,最终,ABD都平衡
有了上面的 做铺垫,下面的代码 就 清晰了
#define LH 1//左子树高
#define EH 0//等高 equal height
#define RH -1//右子树高
//左平衡
void leftBalance(AvlTree * tree){
AvlTree p = *tree;
AvlTree lc = p->lChild;
switch (lc->bf){//
case LH:{//LL型,插入在左子树的左子树上
p->bf = lc->bf = EH;
R_Rotate(tree);
//R_Rotate(tree);尽量按上面来写
//p->bf = lc->bf = EH;
break;
}
case RH:{//LR型,插入在左子树的右子树上
AvlTree rc = lc->rChild;
switch (rc->bf){//设置 tree ,lc的平衡因子
case LH:{//插入在 rc 的 左子树上
p->bf = RH;
lc->bf = EH;
break;
}
case EH:{//这个真没想明白。。。可能是 EH吗
p->bf = lc->bf = EH;
break;
}
case RH:{//插入在rc的右子树上
p->bf = EH;
lc->bf = LH;
break;
}
}
rc->bf = EH;//左子树的右子树 的平衡因子 必为 “等高”
L_Rotate(&(*tree)->lChild);//先左旋转 左子树
R_Rotate(tree);//在右旋转 根节点
break;
}
}
}
RL型: 将 F 插 在 D 节点 后。同样 也有 两种,插入 在 左 (RLL)和 右 (RLR)。同样 算法相同,平衡因子 不同。最终的 根节点 平衡因子 都为0.
基本思路: 先 将 A的 右子树 C右旋,在将 A左旋。
RL L:插入 在 D的 左子树上,A的 平衡因子 为 0,C的 平衡因子因子 为 -1,D为0.
RLR,读者 可以 自己 画出 它的 平衡图来, A的平衡因子 为1,C的平衡因子为0,D为0.
还有一种 只有 只有 图中 节点 的 AC,然后插入 D节点,最终 ACD的平衡因子 都为0.(也就是底下代码 case :EH的情况)
下面 上代码:
//右平衡
void rightBalance(AvlTree * tree){
AvlTree p = *tree;
AvlTree rc = p->rChild;
switch (rc->bf)
{
case LH:{//插入在右子树的 左子树上
AvlTree lc = rc->lChild;
switch (lc->bf){//设置 p,lc的平衡度
case LH:{//插在 lc的左子树上
p->bf = EH;
rc->bf = RH;
break;
}
case EH:{
p->bf = rc->bf = EH;
break;
}
case RH:{//插在lc的右子树上.
p->bf = LH;
rc->bf = EH;
break;
}
}
lc->bf = EH;//右子树的左子树 最终平衡
R_Rotate(&(*tree)->rChild);//先平衡右子树
L_Rotate(tree);//再平衡根节点
break;//就因为少了一个break...调试了半天。。
}
case RH:{//插入在 右子树的 右子树上,左旋转
p->bf = rc->bf = EH;
L_Rotate(tree);
//L_Rotate(tree);
//p->bf = rc->bf = EH;尽量按上面的来写
}
}
}
//返回值:是否需要插入
bool insertAvlTree(AvlTree * tree,TreeType key,bool * taller){
if (*tree == NULL){//查找失败,插入节点
AvlTree p = *tree = (AvlNode *) malloc(sizeof(AvlNode));
p->data = key;
p->lChild = p->rChild = NULL;//插入节点必为叶子节点
p->bf = EH;//并且平衡因子为等高
*taller = true;//不要忘记 设置 长高了..
return true;
}
else{
AvlTree p = *tree;
TreeType data = p->data;
if(data == key){//有相同值时,不需要插入.
return false;
}
else if(data > key){//从左子树里查找
if (insertAvlTree(&p->lChild,key,taller) == false){//有相同值,不需要插入
return false;
}
else if(*taller == true){
switch (p->bf){
case LH:{
leftBalance(tree);
*taller = false;//平衡后,不影响 祖先节点的 平衡度
break;
}
case EH:{//平衡因子为0,插入后平衡因子为“左高”,并设置 长高了
p->bf = LH;
*taller = true;
break;
}
case RH:{//平衡因子为-1,插入后平衡因子为“等高”,并设置 没长高
p->bf = EH;
*taller = false;
break;
}
}
}
return true;
}
else{//从右子树里查找
if (insertAvlTree(&p->rChild,key,taller) == false){//不需要插入
return false;
}
else if (*taller == true){
switch (p->bf){
case LH:{//插入后 “等高”了
p->bf = EH;
*taller = false;
break;
}
case EH:{//插入后,右子树高,设置 长高了
p->bf = RH;
*taller = true;
break;
}
case RH:{
rightBalance(tree);
*taller = false;//平衡后,不影响祖先节点的 平衡因子
break;
}
}
}
return true;
}
}
}在 写完之后, 我们 需要 验证 是否是 AVL树,我们 可以 用 中序 + 层序。
中序: 根据 定义 可知 AVL的中序遍历 必须 从 小 到大的。
层序遍历:打印出 每一层的 节点,看看 他们的 平衡 因子 是否 是 -1,0,1。
如果 你还 不放心,可以 直接 画出 输入结果的 AVL树 ,和 打印出来的 数字 比较一下。相同 的 输入 的 AVL树 是 唯一了。
下面 给出 层序 和 中序的代码:
void inOrderTraverse(AvlTree tree){
if (tree != NULL){
inOrderTraverse(tree->lChild);
printf("%d\t",tree->data);
inOrderTraverse(tree->rChild);
}
}
void levelOrderTraverse(AvlTree tree){
if (tree != NULL){
LinkQueue queue;
queueInit(&queue);
enqueue(&queue,tree);
int count = 1;
int nextCount = 0;
int level = 1;
printf("-----------层序遍历--------------\n");
while (!queueEmpty(queue)){
printf("第%d层数据:",level);
for (int i = 0; i < count; i++){
AvlTree front;
dequeue(&queue,&front);
printf("%d\t",front->data);
if (front->lChild != NULL){
enqueue(&queue,front->lChild);
nextCount++;
}
if (front->rChild != NULL){
enqueue(&queue,front->rChild);
nextCount++;
}
}
printf("\n");
count = nextCount;
nextCount = 0;
level ++;
}
queueDestory(&queue);
}
}
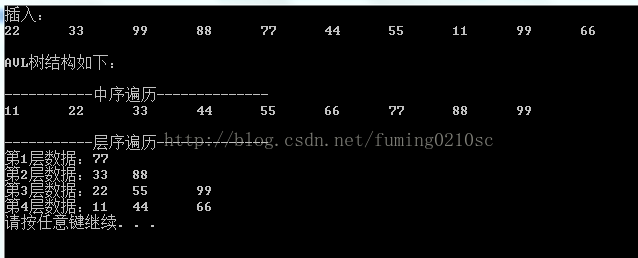
运行截图:
参考网址:点击打开链接
点击打开链接