红黑树的删除
删除思路
经理了插入节点的磨练,接下来就要说红黑树的删除节点了。
在删除红黑树节点时,首先将他当做一个普通的二叉查找树进行删除,分几种情况(暂时不考虑红黑树的定义)
- 被删除节点没有子节点,直接删除
- 被删除节点有子节点,用它的前驱或者后继进行替代
因为上述过程只是按照二叉查找树的方式进行删除了,并没有考虑红黑树的性质,所以删除之后,还需要对照二叉树的性质进行调整(在上述过程中,用来替换被删除位置的节点称为当前节点)
- 如果删除的节点是叶子节点(没有子节点),那么又分为两种子情况
1.1 被删除的节点是红色,无需调整
1.2 被删除节点是黑色,需要调整 - 如果被删除的节点不是叶子节点
2.1 当前节点是红色,将当前节点颜色改为和被删除节点一致即可
2.2 当前节点是黑色,需要调整
上面是对红黑树删除后调整的简单概括,现在针对上述情况,先说为什么需要调整或者不需要调整,然后再说如何调整,还是用图进行说明
情况1.1:被删除的是叶子节点,并且是红节点,例如删除节点343,很显然,删除后和删除前的树都能满足红黑树的定义,所以删除后无需调整
情况1.2:被删除的是叶子节点,并且是黑节点,例如删除节点32,这时被删除的路径上少了一个黑色节点,所以需要进行调整
情况2.1:当前节点是红色,例如删除646节点,这时前驱是580,后继是649,它们都是红色节点,所以不需要调整
情况2.2:当前节点是黑色,例如删除218节点,这时前驱和后继都是黑色节点,所以当前节点一定是黑色节点,所以需要调整
对于被删除节点不是叶子节点时,例如当我们删除646节点时,我们用它的前驱580替代它,然后我们就可以看成删除的是4580节点(这里很重要),或者用后继替代它,然后删除后继节点。
这样的话我们就可以将情况2中的两种情况转换成情况1的两种情况
总结之后就是,最终删除的节点如果是红色节点,那么不需要调整,如果最终删除的节点是黑色节点,那么需要调整
(以上几种情况需要认真思考,只有思考清楚了,才能明白为什么需要调整,以及如何调整)
具体代码
private void deleteEntry(Entry p) {
modCount++;
size--;
//如果p有两个子节点,那么找到替换p的当前节点(前驱或者后继),然后删除它
if (p.left != null && p.right != null) {
Entry s = successor(p);
p.key = s.key;
p.value = s.value;
p = s;
}
//找到被删除的替换节点(如果是前驱或者后继被删除,那么它一定只要一个子节点或者没有子节点)
Entry replacement = (p.left != null ? p.left : p.right);
if (replacement != null) {
//replacement不为空,说明p有且仅有一个子节点,并且p还是黑色,那么用p的子节点替换p
replacement.parent = p.parent;
if (p.parent == null)
root = replacement;
else if (p == p.parent.left)
p.parent.left = replacement;
else
p.parent.right = replacement;
p.left = p.right = p.parent = null;
// 如果被删除的节点是黑色,则需要调整,传入的是替换的节点(当前节点)
if (p.color == BLACK)
fixAfterDeletion(replacement);
} else if (p.parent == null) {
//如果被删除的节点没有父节点,那么就是根节点被删除
root = null;
} else {
//如果被删除的节点没有子节点(或者它的前驱或者后继没有子节点),被删除的节点是黑节点,那么需要平衡调整
if (p.color == BLACK)
fixAfterDeletion(p);
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}
删除的平衡调整
明白了上述描述的删除出现的几种情况,那么我们接着说如果进行平衡调整。因为红黑树删除的平衡调整非常复杂(我看了很多博客都看的一头雾水),所以我们这里一点一点深究
看图说明
- 被删除的是叶子节点,并且颜色是黑色(比如删除32)——需要调整
- 被删除的是叶子节点,并且颜色是红色(比如删除580)——不需要调整
- 被删除的不是叶子节点,并且是黑色(比如删除489或者831)——用它的子树替换,并且将子树的颜色涂黑
看到这里可能有人会问了,怎么可能最后都变成这种情况,其实真的可以,比如
- 删除32,复合情况1
- 删除218,这时用前驱32或者后继232替换它,那么就变成了删除32或323,复合情况1
- 删除334,那么就用前驱232或者后继489替换它,如果用前驱232替换,则直接复合情况1,如果用后继替换,那么就变成了删除489(即情况3),然后用它的子树580替换,删除580节点(复合情况1)
接下来我们先说被删除的是叶子节点,并且是黑色节点时,如何进行平衡调整(重点来了)
平衡调整
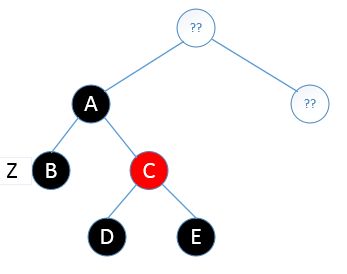
如图,我们要删除一个叶子节点B,它是一个黑色节点
删除之后如下
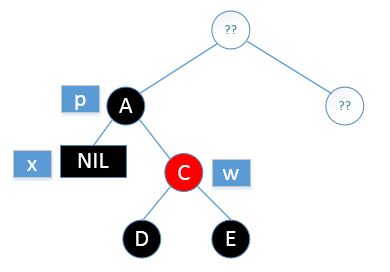
现在x这条路径上少了一个黑色节点,所以我们需要想办法给他增加一个黑色节点,或者其他路径上减少一个黑色节点。
对于这种要删除节点x,它的兄弟节点w是红色的情况,作为情况一
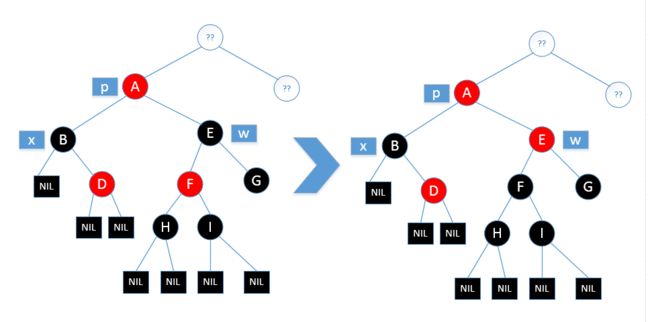
情况一:被删除的节点是黑色节点,它的兄弟节点是红色节点
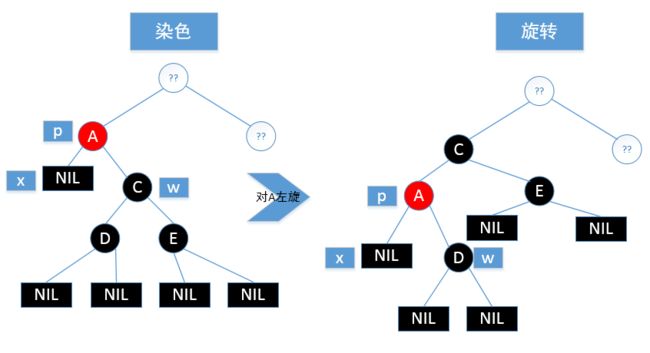
对于情况一,我们的处理方式是将x的兄弟节点w染成黑色,x的父节点p染成红色,并且对p节点进行左旋,如图
这样处理之后,x这条路径上依旧少一个黑色节点,现在的情况是:被删除节点x是黑色,x的兄弟节点w也是黑色,并且w的子节点都是黑色(空节点也是黑色),现在这种情况作为情况二
情况二:被删除节点是黑色,它的兄弟节点是黑色,兄弟节点的子节点也是黑色
对于情况二,我们要知道,现在是x这条路径上少了一个黑色节点(删除的x是黑色的,所以少了一个黑色节点),而x的兄弟是黑色节点.
- 如果x的父节点p是红色节点,那么将兄弟节点的颜色和父节点的颜色互换,即w染成红色,父节点p染成黑色就完成了修复,因为x路径少的一个黑色节点加上了,而w路径上的黑色节点并没有变化
- 如果x的父节点p是黑色,那么就将兄弟节点w染成红色,现在x和w路径上都少了一个黑色节点,所以将p看成一个新的x,进行循环
(这一段有些绕,需要仔细理解)
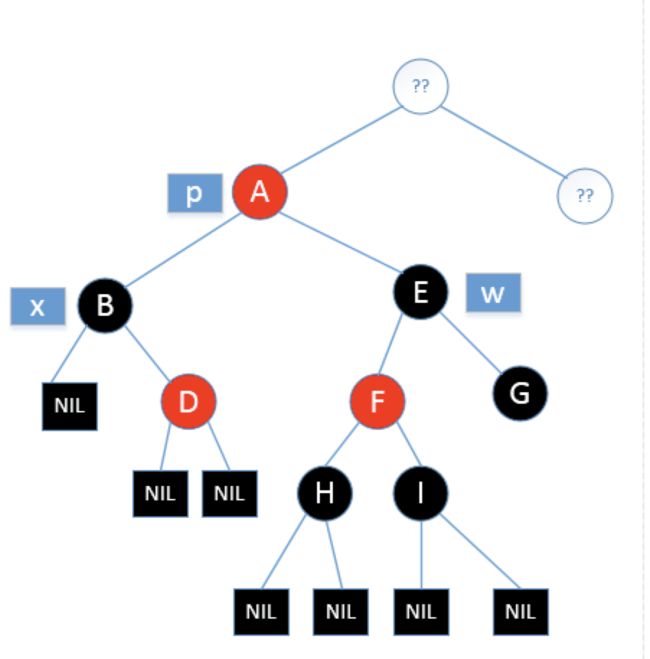
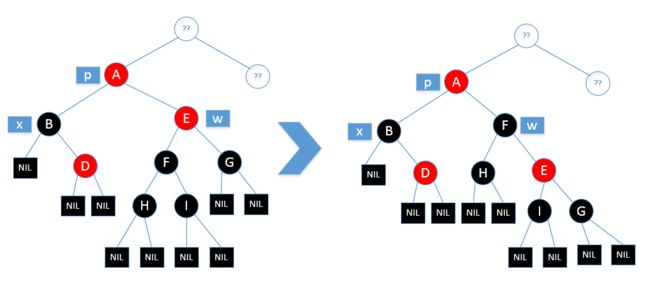
当然,如果被删除的节点是黑色,它的兄弟节点是黑色,兄弟节点的子节点中左孩子是红色,右孩子是黑色(兄弟节点的方向和兄弟节点黑色子孩子的方向一致),比如兄弟节点是父亲的右孩子,那么它的黑色子节点也是右孩子,这种情况就是情况三
情况三:被删除节点是黑色,它的兄弟节点是黑色,兄弟节点的子节点分别是是红色和黑色,并且黑色的方向和兄弟节点的方向一致
如图,这个是删除x子节点进行调节之后出现的中间情况,现在它就是情况三
因为目前x路径上少一个黑色节点,所以我们的目标是向x路径添加一个黑色节点
首先我们将w和它的左孩子交换,这样之后w的右子树上则少了一个黑色节点
接下来我们对w进行右旋,这样w的右子树少的黑色节点就补上了
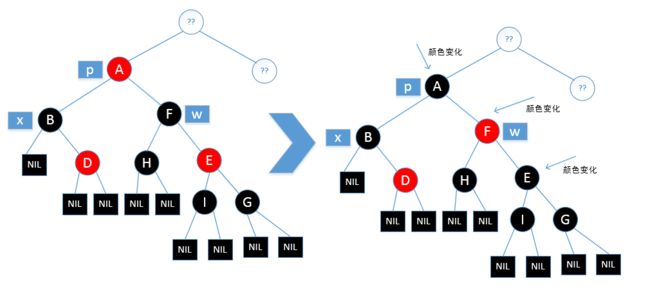
当然,到这里处理还并没有完成,因为x路径上依旧少一个黑色节点,但是这时是一种新的情况即情况四
情况四:x是黑色节点,它的兄弟w是黑色节点,它的孩子分别为红色节点和黑色节点,并且红色节点的方向和自己的方向相同(和情况3是镜像)
明确我们的目标,x路径少一个黑色节点,所以我们需要添加一个黑色节点
这里步骤有些多,所以我们需要明确一下思路
首先x路径是少一个黑节点的,所以我们需要想办法给x路径增加一个黑节点
所以,第一步,将w节点的颜色和p节点的颜色互换
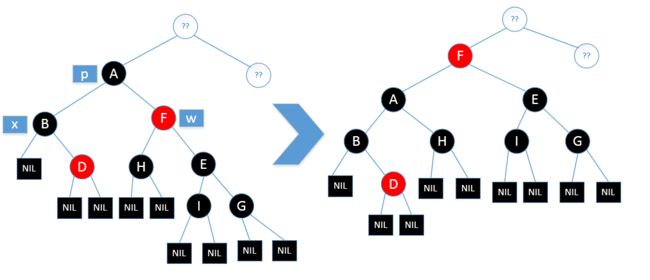
如果p节点是红色,做完这步其实就已经完成修复了,但是如果p节点本来就是黑色的话,我们就需要将p节点再加到x路径的父节点上,所以第二步,对p节点进行左旋,但是左旋之后w的右子节点就少了一个黑节点(因为黑节点p旋转到x路径上去了),所以第三步,将w的右子节点染成黑色如上图
旋转如下:
到此,红黑树的删除修复就已经完成了
具体实现代码如下(已添加详细注释)
private void fixAfterDeletion(Entry x) {
//如果x节点不是根节点,并且x节点是黑色,则进行调整,当x是红色时则无需调整(上文已说明原因)
while (x != root && colorOf(x) == BLACK) {
//如果x是父节点的左子树
if (x == leftOf(parentOf(x))) {
Entry sib = rightOf(parentOf(x));
//保存x的兄弟节点sib
if (colorOf(sib) == RED) {
//如果x的兄弟节点是红色,那么父节点一定是黑色,这时对应情况一
//将兄弟节点设为黑色,父节点设为红色,并对父节点进行一次左旋
setColor(sib, BLACK);
//将x的父节点设置为红色
setColor(parentOf(x), RED);
//对x的父节点进行左旋
rotateLeft(parentOf(x));
//拿到新的兄弟节点
sib = rightOf(parentOf(x));
}
//因为兄弟节点是红色的情况上面已经处理过了,处理之后的兄弟节点必定是黑色,所以这里开始兄弟节点颜色都是黑色
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
//兄弟节点是黑色,并且兄弟节点的两个子节点都是黑色,即情况二
//这里设置兄弟节点为红色
setColor(sib, RED);
//取出x的父节点,如果是红色则会退出循环,再将父节点设为黑色(代码在最后面)
//如果父节点本来就是黑色,则会再次进入循环
x = parentOf(x);
} else {
if (colorOf(rightOf(sib)) == BLACK) {
//如果兄弟节点是黑色,兄弟节点是右节点是黑色,对应情况三
//将左节点设置黑色,兄弟节点设为红色,然后对兄弟节点进行右旋(原因上文已描述)
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
rotateRight(sib);
//取出新的兄弟节点
sib = rightOf(parentOf(x));
}
//经过了情况三的处理,就会变成情况四
//将兄弟节点的父节点和兄弟节点颜色互换,然后设置兄弟节点的右子节点为黑色,最后左旋父节点,完成修复
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(rightOf(sib), BLACK);
rotateLeft(parentOf(x));
x = root;
}
} else { // 下面则是镜像情况,用相反的逻辑处理即可
Entry sib = leftOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
setColor(x, BLACK);
}
注:以上图片大部分来自网络,侵删
数据结构导读目录