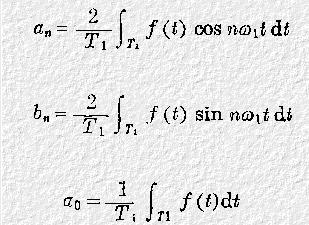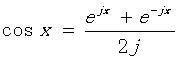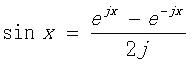频率域上的图像增强

http://download1.csdn.net/down3/20070617/17204050839.rar

本人同意他人对我的文章引用，但请在引用时注明出处，谢谢．作者：蒋志强

相应的PDF文档及可执行程序可以在http://download.csdn.net/source/190027下载

1频率图像增强的简介

1．1背景介绍：

在数字图像处理中，图像最直观的理解是把图像理解为二维函数F(x,y)，其中x，y作为数字图像中象素的二维空间的坐标，F的值作为数字图像象素该位置的灰度值。但是在空间域在处理某些数字图像的问题时，会比较困难甚至是几乎难以处理。在频率下处理的时候，同样的问题用不同的描述方式是和空间域的表示是等价的，但由于描述方式不同了以前空间上很难处理的问题在频率域上就有可能变得很容易了。在频率域上处理时，还可以使用数字信号处理的一系列成熟的方法，让我们处理特殊的问题有了很多的工具，所以频率图像增强是很有价值进行学习和研究的。

1．2频率图像增强的基本步骤：

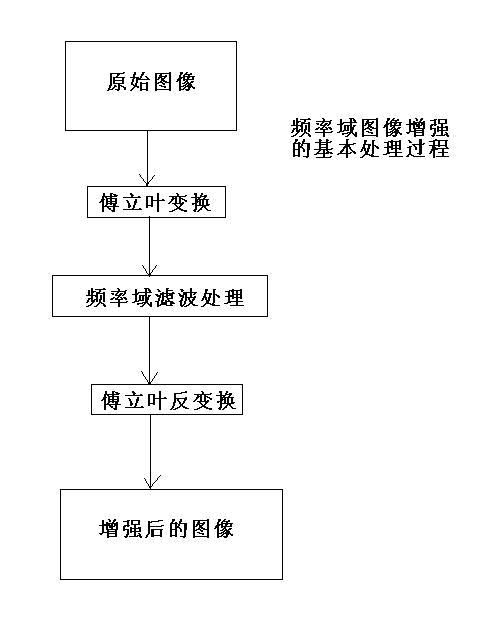
无论是何种类型，何种目的的频率域图像增强，处理的过程都是基本一致的，并如下图1-1所示:

图1-1

1．3关于傅立叶变换:

在图1-1中,在具体进行频率域的各种处理滤波的前后,进行了傅立叶变换以及傅立叶反变换.这两个变换的过程就是将空间的信息分解为在频率上的表示,或者将频率上的表示转化为空间上的表示,两种变换是互为逆变换的.正是通过傅立叶正反变换的处理,才使得频率域上的处理可以用于图像的增强。

2．关于傅立叶变换的理解：

2．1关于傅立叶级数:

在自然科学和工程技术，时常会遇到各种周期现象，在数学上都可以用周期函数来描述。正弦函数或余弦函数是周期函数中最简单的，我们对正弦/余弦函数比较容易处理，如果可以将复杂的周期函数表示成简单的正弦/余弦周期函数的形式，将会对我们处理问题带来很大的方便。数学家傅立叶在这方面的贡献就是提出了将复杂的周期函数表示为简单的正弦/余弦周期函数，并提出了进行这种转变的前提条件----狄里赫利条件。

傅立叶级数：

在这个公式中

其中的函数f(t)是一般的周期函数，这样我们就可以实现了转换为了简单正弦/余弦周期函数的形式了。上面的傅立叶级数表示了一个周期函数，如何表示成无穷多个正余弦函数叠加的形式的方法。

2．2傅立叶级数与傅立叶变换的联系：

在任何一本数字图像的书都可以找到下面的一纬傅立叶变换的公式的表示：

其中f(x)是一个普通的非周期函数，j = ，大写的F表示傅立叶变换,我们对比这个式子与傅立叶级数公式，会发现有很大的差别，但实际上他们的思想是相同的。现在我们试图从傅立叶级数推到傅立叶变换的公式，以证明他们的联系，并通过推导过程比较深入的理解傅立叶公式在图像处理中的物理意义，做到知其然，也知其所以然。

数学中有个叫做欧拉公式的数学表达： ；

其中的j = ；

反解欧拉公式可以得到：

  

                

通过反解欧拉公式得到的COSX及SINX复数形式的指数表示，将其代入傅立叶级数公式中可以得到下面的傅立叶级数公式的指数表示形式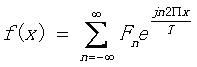

其中f(x)表示一个一般的周期函数，并且周期为T，j =。

其中 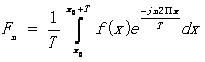，这个式子中的积分从 到 ，因为积分的区域是f(x)的一个周期T，所以 可以周期中的任意值，对结果没有任何影响。

傅立叶级数公式的指数形式和三角函数形式是等价的，我们注意到指数形式中的 项与傅立叶变换公式在形式上非常相象。因为是可以取任意值的，不妨取为 ，于是就有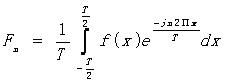  。这样的做的前提f(x)是周期为T的周期函数，但是在现实中的函数往往不是直接的周期函数，但非周期函数可以理解为周期 的特殊推广。在上式子中我们令 ，于是便有等式 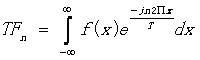。这样表示的前提是f(x)不是一个周期函数（或者说是特殊周期为 的周期函数）， 。我们发现 的形式很接近傅立叶变换公式了。

现在我们再令，并将其带入 的表示中，便有：

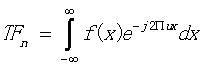     ，很惊喜吧，这样就和傅立叶变换公式的形式一模一样了。是表示上的巧合还是真正的在数学上具有意义的呢？下面我们马上来理解这样进行的数学变换是否是有意义的。

2．3对傅立叶变换的理解：

在傅立叶变换中的u表示的频率，在上面的数学变换中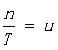，将，这样代换后的u是否也表示频率呢?

因为T是周期，所以 就是频率。，所以 是个无穷小的量，可以理解为最小的基本频率单位，而n是可以取从 到 的值，所以 应该是可以表示 到 的频率。

当频率为负数时也是有意义的，因为周期可正可负，对于周期函数，相同数值的正周期和相同数值的负周期是等价的，所以负频率和相同数值的正频率也是等价的。当n给定一个具体的值时，由于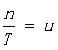，就给定了一个特定的频率, (或者说傅立叶变换公式)的右边就表示了函数f(x)中该特定频率的部分。

2．4快速傅立叶变换FFT

将数字图像作为二纬函数f(x,y)通过傅立叶变换，转换到频率域上以后就可以根据具体需要进行各种滤波处理了，完成滤波后在通过反变换就可以得到特定增强滤波处理后的图像了。但实际上傅立叶变换的算法复杂度是很高的，处理的效率很低，对于一纬函数f(x)，如果有M个点，则需要进行 次的乘法运算，而且我们知道乘法运算的在CPU上执行的效率并不高。于是快速傅立叶变换就显得特别的有用了，通过一系列的数学上的技巧和等价，进行相同的一纬M个点的变换FFT只需要进行 次的相同运算。FFT算法比标准的傅立叶变换算法的效率要高 倍，当M增大时，FFT的优势将迅速变得非常巨大。当M为256个点时，FFT要比标准傅立叶变换快106倍；当M为1024个点时，FFT要快340倍；当M为65536个点时，FFT要快13625倍！！！

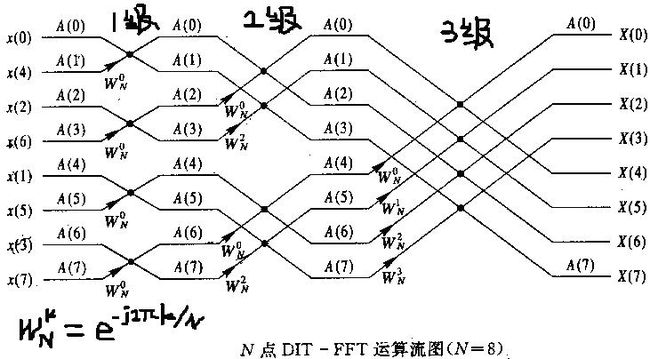
FFT算法的基本思想如下图1-2所示：

图1-2

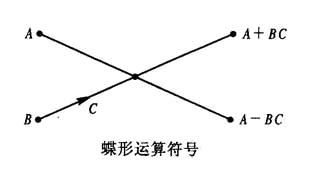
上图是8个点的FFT处理过程，又称为蝶形算法。因为每一级的处理都上下交叉，每个交叉处就像一只蝴蝶一样。每个交叉处的处理过程如图1-3所示：

图1-3

3频率域滤波

3．1滤波的基本原理

原始图像的二维函数被分解为不同频率的信号后，高频的信号携带了图像的细节部分信息(比如图像的边界)，低频的信号包含了图像的粗糙背景信息。对这些不同频率的信号，进行处理就可以实现相应的加强图像的目的。例如让低频信号加强，可以让图像细节对比加强，达到锐化的效果，去掉低频就可以把细节部分剔除，仅仅得到大致背景轮廓的图像。

3．2常用的基本滤波器

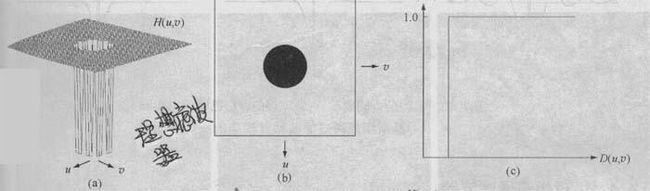
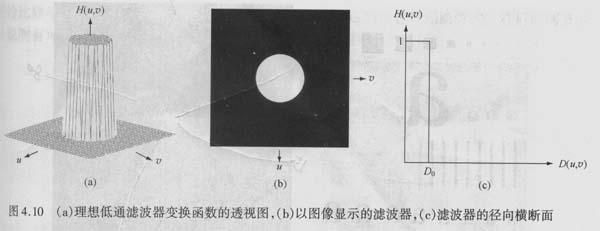
最常用的有理想高通滤波器（如图1- 4所示），理想低通滤波器(如图1-5所示)。理想高通滤波器让低于某个指定门限值频率的信号全部为零，其它频率的信号保持不变；理想低通滤波器让高于某个门限值频率的信号全部为零。

图1-4     理想高通滤波器

图1-5     理想低通滤波器

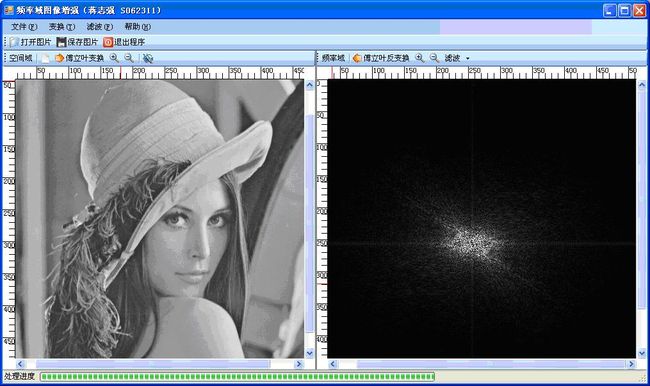
在编写程序实现前，可以预先判断理想低通滤波器将模糊细节。对于512*512大小的标准图像lena，设置门限值频率为40。处理前的效果如图1-6，右边是频率域的图像表示。

图1-6

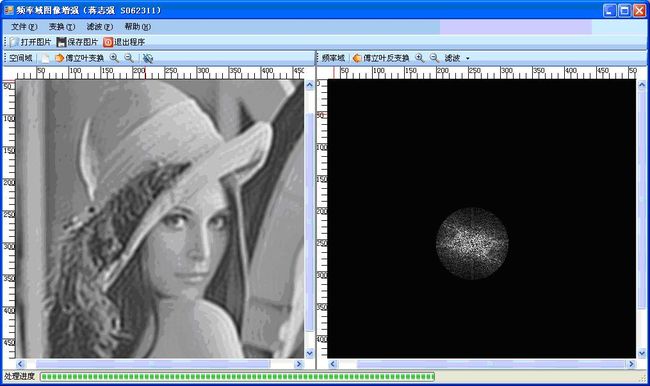
进行滤波处理后的效果如图1-7所示，注意到频率的图像的中心40半径以外的部分是全黑的，因为滤波器将大于40频率的信号全部变为了零。

图1-7

为了便于更清晰对比，将滤波后的图像与滤波前的图像放大2倍进行比对如图1-8所示：

图1-8

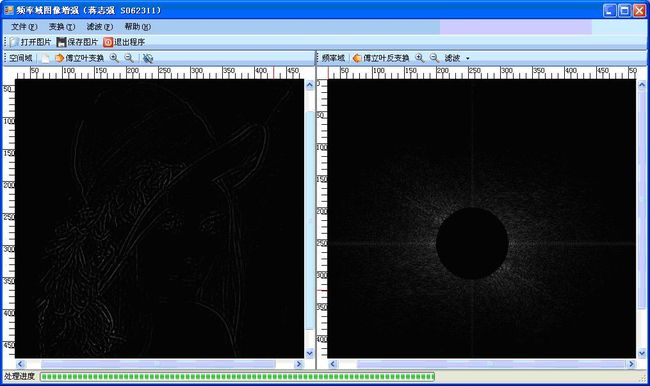
对于理想高通滤波器，过滤掉低频信号后，大的背景低色信息将会丢失只留下图像边缘轮廓的信息，设置门限值频率为40，处理后的效果如图1-9所示：

 

图1-9

4结论

本课程报告比较细致的数学上分析了傅立叶变换，并通过数学上的讨论去进一步理解傅立叶变换，比较深入的理解了傅立叶变换以及建立在该变换基础之上的数字图像在频率域上的增强。最后自己编程实现了FFT及反FFT算法，在程序中实现了两种最基本的滤波器，比较扎实的掌握了这部分的知识。

 

 

 

 

 

5参考文献

[1]Rafael C. Gonzalez, Richard E. Woods, Digital Image Processing Second Edition, 2005

[2]杨志和, 微积分, 2002

[3]陈生潭, 郭宝龙, 信号与系统 第二版, 2001

[4]燕庆明, 信号与系统教程, 2004

[5]Kenneth. R. Castleman, Digital Image Processing, 1998

[6]何东健, 耿楠, 数字图像处理, 2003