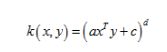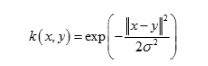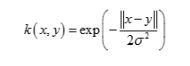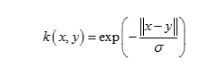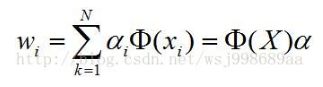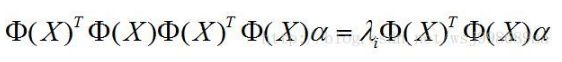1、TabLayout与Fragment结合使用的常见方式通常会使用FragmentPagerAdapter或FragmentStatePagerAdapter与ViewPager配合,再将TabLayout与ViewPager关联,实现通过TabLayout切换Fragment。以下是布局文件示例activity_main.xml:
刘萍萍老师《基于新课标的情境活动与学习任务群设计策略》学习
青箬笠0
刘萍萍新乡市基础教育教学研究室“让学生直接思考真实问题有助于激发和唤醒学生的理解。”(「美]格兰特·威金斯·「美」杰伊·麦克泰格《追求理解的教学设计》P44)所以要设计情境活动。一、情境活动与学习任务群概念从何而来“考试命题应以情境为载体,依据学生在真实情境下解决问题的过程和结果评定其素养水平。日常生活情境指向真实具体的社会生活,关注学生在生活场景中的语言实践,凸显语言交际活动的对象、目的和表述方
淘宝上的无门槛优惠券是什么意思?淘宝无门槛优惠券怎么抢
好项目高省
淘宝上的无门槛优惠券是指消费者在购物时,不需要满足特定的消费金额、购买商品类别、消费次数等条件,就可以直接使用的优惠券,以享受一定的折扣或优惠。这种优惠券的使用限制较少,为消费者提供了更大的灵活性和实惠。具体来说,无门槛优惠券的特点包括:无消费金额限制:与有门槛优惠券(如满减券)不同,无门槛优惠券没有消费金额的要求,无论购买商品的金额多少都可以使用。适用范围可能较窄:虽然无门槛优惠券在使用上更为灵
来宾亲子鉴定准确度高吗?来宾上户口亲子鉴定怎么做【附最新办理流程】
中正DNA鉴定中心
来宾亲子鉴定准确度高吗?在广西来宾做亲子鉴定准确度非常高,只要选择正规有资质的鉴定机构,出具结果是有保障的,不管是个人隐私还是司法用途,虽然办理流程和报告用途有区别,检测实验流程一样,准确度非常精准。有关来宾上户口亲子鉴定怎么做也是咨询比较多的话题,下面第四点详细解答。一、亲子鉴定的方法亲子鉴定是目前最科学、准确的判断亲子关系的方法,依赖DNA分析技术,对比测序样本DNA后,实验室内精确辨识个体与
Valentino耳饰怎么买便宜?便宜又好看女生耳钉在哪买
直返APP拼多多优惠券
在时尚的世界里,Valentino耳饰以其独特的设计和精湛的工艺,成为了众多时尚爱好者追捧的焦点。今天,让我们一同来领略Valentino耳饰的魅力所在。Valentino耳饰是对优雅与时尚的完美诠释。每一款耳饰都仿佛是一件艺术品,精心雕琢,细节之处尽显匠心。从华丽的宝石镶嵌到精致的金属纹理,每一个元素都在诉说着品牌的奢华与独特。戴上Valentino耳饰,瞬间便能提升整体造型的档次与气质。无论是
京东618最省钱的攻略,超级大红包领取方法!
氧惠好物
现在京东一年一度的购物节马上就要来了,就是京东618购物活动了。那么京东的618活动一般什么时候去买是最划算?有什么优惠活动?下面给大家讲述一下。京东将618的活动分为预热期-专场期-高潮期-返场期京东密令红包:最爱领红包828红包多多148购物、看电影、点外卖、用氧惠APP!更优惠!氧惠(全网优惠上氧惠)——是与以往完全不同的抖客+淘客app!2023全新模式,我的直推也会放到你下面,送1:1超
唯品会如何免5元运费?唯品会无门槛优惠券免费领取是真的吗
日常购物小技巧
揭秘唯品会免5元运费秘籍与无门槛优惠券使用方法在电商时代,优惠券和免运费活动层出不穷,吸引着广大消费者。唯品会作为一家知名的电商平台,也时常推出各种优惠活动。本文将为您揭秘如何在唯品会免5元运费以及无门槛优惠券免费领取的使用方法。一、唯品会免5元运费攻略1.会员专享:唯品会会员可享受免5元运费的优惠。而非会员则需支付5元运费。因此,建议用户在购物时优先考虑是否需要购买会员。2.活动参与:唯品会时常
怎样挑到一件好的高仿maxmara羽绒服?
高端顶级奢侈品
怎样挑到一件好的高仿maxmara羽绒服?MaxMara是意大利风格的象征标志,其成衣系列独具高级定制女装的剪裁设计、奢华材质以及精致细节,彰显了这一品牌系列的优雅自信与现代品味。MaxMara由极富远见的AchilleMaramotti创立于1951年,以其时尚的外套、简约的单品、干练的西装和优雅的配饰而闻名。MaxMara系列如今远销90多个国家和地区,共有2254个销售网点,而且是MaxMa
Gson、Fastjson 和 Jackson 对比解析
小张0.0
JavaWebjson
目录1.Gson(Google)基本介绍:核心功能:特点:使用场景:2.Fastjson(Alibaba)基本介绍:核心功能:特点:使用场景:3.Jackson基本介绍:核心功能:特点:使用场景:4.对比总结5.选择建议Gson、Fastjson和Jackson这三种都是Java生态中广泛使用的JSON处理库,用于实现Java对象与JSON数据之间的相互转换。在项目中使用不同的方法即可调用不同的J
redis-plus-plus安装与使用
Yu_Lijing
redis数据库缓存
目录一.安装hiredis二.接口三.使用四.总结C++操作redis的库有很多.咱们使用redis-plus-plus.这个库的功能强大,使用简单.Github地址:https://github.com/sewenew/redis-plus-plus一.安装hiredisredis-plus-plus是基于hiredis实现的.hiredis是一个C语言实现的redis客户端.因此需要先安装hi
10分钟搞定 MinIO 单节点多磁盘部署!打造稳定高可用对象存储【二】
MinIO是一个**高性能、开源的对象存储系统**,主要用于存储非结构化数据(如图片、视频、文档、备份等),与AmazonS3完全兼容。它被广泛用于云原生应用、大数据分析、AI模型存储、容器平台(如Kubernetes)等场景。MinIO支持多种部署模式,其中:单节点单磁盘(Single-NodeSingle-Drive)模式适用于开发测试、小规模应用或资源受限的场景。它的部署简单,不依赖集群、分
收视率怎么赚钱?这篇文章为你揭秘电视剧怎么赚钱的
氧惠全网优惠
现在的人们几乎都是有刷剧的习惯,我们忙完了一天的工作以后都是会看上有些东西,也是成为了我们生活当中必不可少的一个娱乐项目,甚至好多人为了看电视剧可以熬一整个通宵,目的就是看到他们最后的大结局。氧惠APP是与以往完全不同的抖客+淘客app!2024全新模式,我的直推也会放到你下面。主打:带货高补贴,深受各位带货团队长喜爱(训练营导师每天出单带货几万单)。注册即可享受高补贴+0撸+捡漏等带货新体验。古
设计模式介绍
tntxia
设计模式
设计模式来源于土木工程师 克里斯托弗 亚历山大(http://en.wikipedia.org/wiki/Christopher_Alexander)的早期作品。他经常发表一些作品,内容是总结他在解决设计问题方面的经验,以及这些知识与城市和建筑模式之间有何关联。有一天,亚历山大突然发现,重复使用这些模式可以让某些设计构造取得我们期望的最佳效果。
亚历山大与萨拉-石川佳纯和穆雷 西乐弗斯坦合作
android高级组件使用(一)
百合不是茶
androidRatingBarSpinner
1、自动完成文本框(AutoCompleteTextView)
AutoCompleteTextView从EditText派生出来,实际上也是一个文本编辑框,但它比普通编辑框多一个功能:当用户输入一个字符后,自动完成文本框会显示一个下拉菜单,供用户从中选择,当用户选择某个菜单项之后,AutoCompleteTextView按用户选择自动填写该文本框。
使用AutoCompleteTex
[网络与通讯]路由器市场大有潜力可挖掘
comsci
网络
如果国内的电子厂商和计算机设备厂商觉得手机市场已经有点饱和了,那么可以考虑一下交换机和路由器市场的进入问题.....
这方面的技术和知识,目前处在一个开放型的状态,有利于各类小型电子企业进入
&nbs
自写简单Redis内存统计shell
商人shang
Linux shell统计Redis内存
#!/bin/bash
address="192.168.150.128:6666,192.168.150.128:6666"
hosts=(${address//,/ })
sfile="staticts.log"
for hostitem in ${hosts[@]}
do
ipport=(${hostitem
单例模式(饿汉 vs懒汉)
oloz
单例模式
package 单例模式;
/*
* 应用场景:保证在整个应用之中某个对象的实例只有一个
* 单例模式种的《 懒汉模式》
* */
public class Singleton {
//01 将构造方法私有化,外界就无法用new Singleton()的方式获得实例
private Singleton(){};
//02 申明类得唯一实例
priva
springMvc json支持
杨白白
json springmvc
1.Spring mvc处理json需要使用jackson的类库,因此需要先引入jackson包
2在spring mvc中解析输入为json格式的数据:使用@RequestBody来设置输入
@RequestMapping("helloJson")
public @ResponseBody
JsonTest helloJson() {
android播放,掃描添加本地音頻文件
小桔子
最近幾乎沒有什麽事情,繼續鼓搗我的小東西。想在項目中加入一個簡易的音樂播放器功能,就像華為p6桌面上那麼大小的音樂播放器。用過天天動聽或者QQ音樂播放器的人都知道,可已通過本地掃描添加歌曲。不知道他們是怎麼實現的,我覺得應該掃描設備上的所有文件,過濾出音頻文件,每個文件實例化為一個實體,記錄文件名、路徑、歌手、類型、大小等信息。具體算法思想,
oracle常用命令
aichenglong
oracledba常用命令
1 创建临时表空间
create temporary tablespace user_temp
tempfile 'D:\oracle\oradata\Oracle9i\user_temp.dbf'
size 50m
autoextend on
next 50m maxsize 20480m
extent management local
25个Eclipse插件
AILIKES
eclipse插件
提高代码质量的插件1. FindBugsFindBugs可以帮你找到Java代码中的bug,它使用Lesser GNU Public License的自由软件许可。2. CheckstyleCheckstyle插件可以集成到Eclipse IDE中去,能确保Java代码遵循标准代码样式。3. ECLemmaECLemma是一款拥有Eclipse Public License许可的免费工具,它提供了
Spring MVC拦截器+注解方式实现防止表单重复提交
baalwolf
spring mvc
原理:在新建页面中Session保存token随机码,当保存时验证,通过后删除,当再次点击保存时由于服务器端的Session中已经不存在了,所有无法验证通过。
1.新建注解:
? 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
《Javascript高级程序设计(第3版)》闭包理解
bijian1013
JavaScript
“闭包是指有权访问另一个函数作用域中的变量的函数。”--《Javascript高级程序设计(第3版)》
看以下代码:
<script type="text/javascript">
function outer() {
var i = 10;
return f
AngularJS Module类的方法
bijian1013
JavaScriptAngularJSModule
AngularJS中的Module类负责定义应用如何启动,它还可以通过声明的方式定义应用中的各个片段。我们来看看它是如何实现这些功能的。
一.Main方法在哪里
如果你是从Java或者Python编程语言转过来的,那么你可能很想知道AngularJS里面的main方法在哪里?这个把所
[Maven学习笔记七]Maven插件和目标
bit1129
maven插件
插件(plugin)和目标(goal)
Maven,就其本质而言,是一个插件执行框架,Maven的每个目标的执行逻辑都是由插件来完成的,一个插件可以有1个或者几个目标,比如maven-compiler-plugin插件包含compile和testCompile,即maven-compiler-plugin提供了源代码编译和测试源代码编译的两个目标
使用插件和目标使得我们可以干预
【Hadoop八】Yarn的资源调度策略
bit1129
hadoop
1. Hadoop的三种调度策略
Hadoop提供了3中作业调用的策略,
FIFO Scheduler
Fair Scheduler
Capacity Scheduler
以上三种调度算法,在Hadoop MR1中就引入了,在Yarn中对它们进行了改进和完善.Fair和Capacity Scheduler用于多用户共享的资源调度
2. 多用户资源共享的调度
Nginx使用Linux内存加速静态文件访问
ronin47
Nginx是一个非常出色的静态资源web服务器。如果你嫌它还不够快,可以把放在磁盘中的文件,映射到内存中,减少高并发下的磁盘IO。
先做几个假设。nginx.conf中所配置站点的路径是/home/wwwroot/res,站点所对应文件原始存储路径:/opt/web/res
shell脚本非常简单,思路就是拷贝资源文件到内存中,然后在把网站的静态文件链接指向到内存中即可。具体如下:
关于Unity3D中的Shader的知识
brotherlamp
unityunity资料unity教程unity视频unity自学
首先先解释下Unity3D的Shader,Unity里面的Shaders是使用一种叫ShaderLab的语言编写的,它同微软的FX文件或者NVIDIA的CgFX有些类似。传统意义上的vertex shader和pixel shader还是使用标准的Cg/HLSL 编程语言编写的。因此Unity文档里面的Shader,都是指用ShaderLab编写的代码,然后我们来看下Unity3D自带的60多个S
CopyOnWriteArrayList vs ArrayList
bylijinnan
java
package com.ljn.base;
import java.util.ArrayList;
import java.util.Iterator;
import java.util.List;
import java.util.concurrent.CopyOnWriteArrayList;
/**
* 总述:
* 1.ArrayListi不是线程安全的,CopyO
内存中栈和堆的区别
chicony
内存
1、内存分配方面:
堆:一般由程序员分配释放, 若程序员不释放,程序结束时可能由OS回收 。注意它与数据结构中的堆是两回事,分配方式是类似于链表。可能用到的关键字如下:new、malloc、delete、free等等。
栈:由编译器(Compiler)自动分配释放,存放函数的参数值,局部变量的值等。其操作方式类似于数据结构中
回答一位网友对Scala的提问
chenchao051
scalamap
本来准备在私信里直接回复了,但是发现不太方便,就简要回答在这里。 问题 写道 对于scala的简洁十分佩服,但又觉得比较晦涩,例如一例,Map("a" -> List(11,111)).flatMap(_._2),可否说下最后那个函数做了什么,真正在开发的时候也会如此简洁?谢谢
先回答一点,在实际使用中,Scala毫无疑问就是这么简单。
mysql 取每组前几条记录
daizj
mysql分组最大值最小值每组三条记录
一、对分组的记录取前N条记录:例如:取每组的前3条最大的记录 1.用子查询: SELECT * FROM tableName a WHERE 3> (SELECT COUNT(*) FROM tableName b WHERE b.id=a.id AND b.cnt>a. cnt) ORDER BY a.id,a.account DE
HTTP深入浅出 http请求
dcj3sjt126com
http
HTTP(HyperText Transfer Protocol)是一套计算机通过网络进行通信的规则。计算机专家设计出HTTP,使HTTP客户(如Web浏览器)能够从HTTP服务器(Web服务器)请求信息和服务,HTTP目前协议的版本是1.1.HTTP是一种无状态的协议,无状态是指Web浏览器和Web服务器之间不需要建立持久的连接,这意味着当一个客户端向服务器端发出请求,然后We
判断MySQL记录是否存在方法比较
dcj3sjt126com
mysql
把数据写入到数据库的时,常常会碰到先要检测要插入的记录是否存在,然后决定是否要写入。
我这里总结了判断记录是否存在的常用方法:
sql语句: select count ( * ) from tablename;
然后读取count(*)的值判断记录是否存在。对于这种方法性能上有些浪费,我们只是想判断记录记录是否存在,没有必要全部都查出来。
对HTML XML的一点认识
e200702084
htmlxml
感谢http://www.w3school.com.cn提供的资料
HTML 文档中的每个成分都是一个节点。
节点
根据 DOM,HTML 文档中的每个成分都是一个节点。
DOM 是这样规定的:
整个文档是一个文档节点
每个 HTML 标签是一个元素节点
包含在 HTML 元素中的文本是文本节点
每一个 HTML 属性是一个属性节点
注释属于注释节点
Node 层次
jquery分页插件
genaiwei
jqueryWeb前端分页插件
//jquery页码控件// 创建一个闭包 (function($) { // 插件的定义 $.fn.pageTool = function(options) { var totalPa
Mybatis与Ibatis对照入门于学习
Josh_Persistence
mybatisibatis区别联系
一、为什么使用IBatis/Mybatis
对于从事 Java EE 的开发人员来说,iBatis 是一个再熟悉不过的持久层框架了,在 Hibernate、JPA 这样的一站式对象 / 关系映射(O/R Mapping)解决方案盛行之前,iBaits 基本是持久层框架的不二选择。即使在持久层框架层出不穷的今天,iBatis 凭借着易学易用、
C中怎样合理决定使用那种整数类型?
秋风扫落叶
c数据类型
如果需要大数值(大于32767或小于32767), 使用long 型。 否则, 如果空间很重要 (如有大数组或很多结构), 使用 short 型。 除此之外, 就使用 int 型。 如果严格定义的溢出特征很重要而负值无关紧要, 或者你希望在操作二进制位和字节时避免符号扩展的问题, 请使用对应的无符号类型。 但是, 要注意在表达式中混用有符号和无符号值的情况。
&nbs
maven问题
zhb8015
maven问题
问题1:
Eclipse 中 新建maven项目 无法添加src/main/java 问题
eclipse创建maevn web项目,在选择maven_archetype_web原型后,默认只有src/main/resources这个Source Floder。
按照maven目录结构,添加src/main/ja
(二)androidpn-server tomcat版源码解析之--push消息处理
spjich
javaandrodipn推送
在 (一)androidpn-server tomcat版源码解析之--项目启动这篇中,已经描述了整个推送服务器的启动过程,并且把握到了消息的入口即XmppIoHandler这个类,今天我将继续往下分析下面的核心代码,主要分为3大块,链接创建,消息的发送,链接关闭。
先贴一段XmppIoHandler的部分代码
/**
* Invoked from an I/O proc
用js中的formData类型解决ajax提交表单时文件不能被serialize方法序列化的问题
中华好儿孙
JavaScriptAjaxWeb上传文件FormData
var formData = new FormData($("#inputFileForm")[0]);
$.ajax({
type:'post',
url:webRoot+"/electronicContractUrl/webapp/uploadfile",
data:formData,
async: false,
ca
mybatis常用jdbcType数据类型
ysj5125094
mybatismapperjdbcType
MyBatis 通过包含的jdbcType
类型
BIT FLOAT CHAR