哈夫曼树的建立、编码以及带权路径长(WPL值)的计算

参考文章：https://blog.csdn.net/sspumyl/article/details/53467604 （哈夫曼树的建立、编码以及WPL值的计算）

说明：此文是对参考文章的补充和完善。

  ——————————————————————————————————————————————  

1. 什么是哈夫曼树(Huffman Tree)？

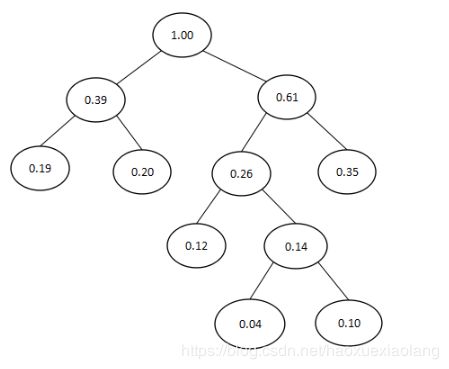
      给定n个权值作为n个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。比如下图。

    （通俗说法：没有度为1的节点，称为最优二叉树，也称为哈夫曼树）

                                      

2. 哈夫曼树的建立、编码以及带权路径长(WPL值)的计算

       假设用于通信的电文由字符集{A，B，C，D，E，F}中的字母构成，这些字母在电文中出现的概率分别为{0.10，0.19，0.20，0.35，0.12，0.04}。

要求：
1、构造一棵Huffman树（要求：左结点的权不大于右结点的权）
2、求各字符对应的Huffman编码
3、求带权路径长度（WPL）

解析：
（1）哈夫曼树的构造

首先，将电文概率由小到大依次排序： 0.04，0.10，0.12，0.19，0.20，0.35。

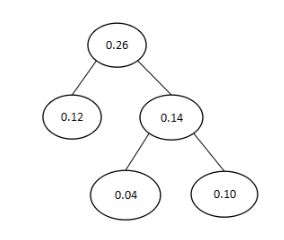
然后，将0.04和0.10作为左子树，右子树构成一棵树。如下图所示：    
                                                

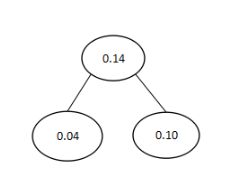
它们根节点之和作为新的结点，排除刚才两个结点，加入新结点0.14重新由小到大依次排序：0.12，0.14，0.19，0.20，0.35
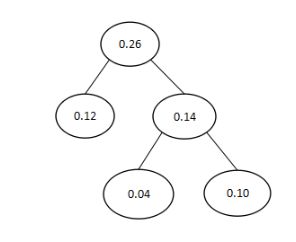
将最小的两个结点作为左子树、右子树构成新的树。如下图所示：

                                                

 排除刚才两个结点，加入新结点0.26，重新排序由小到大依次排序： 0.19，0.20，0.26，0.35。
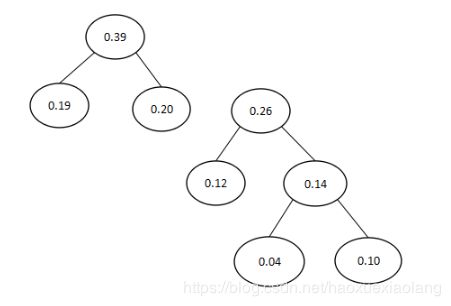
将此时最小的两个结点作为左右子树，建立新的树。如下图所示：

                                                 

排除刚才两个结点，加入新结点0.39，重新排序：0.26，0.35，0.39
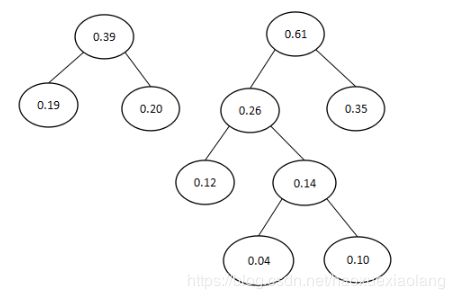
将此时最小的两个结点作为左右子树，建立新的树。如下图所示：

                                             

 

至此只剩下两个结点，构成满足条件的树。则建立的哈夫曼树(Huffman Tree)如下图所示：

                                                

（2）求各字符对应的哈夫曼编码

       《数据结构与算法》课本案例

                        

---

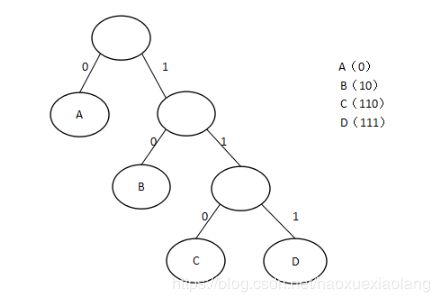
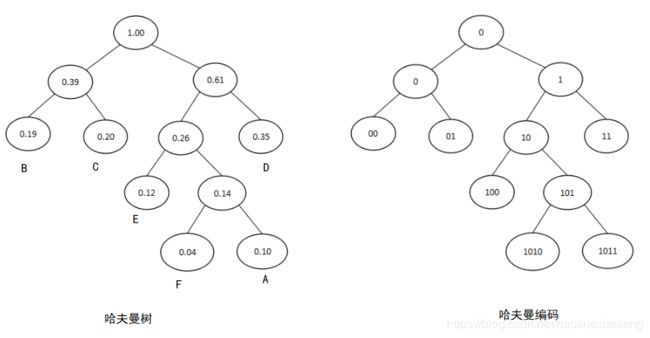
    于是，通俗来理解，  哈夫曼编码 —— 左分支为”0”，右分支为”1”。于是题目的哈夫曼编码示意图如下图。

     已知条件 ： {A，B，C，D，E，F}  =  {0.10，0.19，0.20，0.35，0.12，0.04}。

对比两张图，得到对应字符的哈夫曼编码如下：

    A：1011        B： 00         C：01      D：11         E：100    F：1010

 

（3）带权路径长(WPL值)的计算

       首先给出路径和路径长度的概念，从树中一个结点到另一个结点之间的分支构成这两个结点之间的路径，路径上的分支数目称作路径长度。树的路径长度是从树根到每一结点的路径长度之和。
       树的带权路径长度为树中所有叶子结点的带权路径长度之和，通常记作WPL.

      计算带权路径长度：结点的带权路径长度为从根结点到该结点之间的路径长度与该结点的权的乘积。

     于是，题目的带权路径长度WPL ＝ (0.19 + 0. 20 + 0.35) * 2 + 0.12 * 3 + (0.04 + 0.10) * 4 = 2.4

 

【拓展笔试案例】权值分别为9、3、2、8的结点，构造一棵哈夫曼树，该树的带权路径长度是？

             

一、对结点排序，为2，3，8，9

二、2和3的父节点为5（2+3的权值）

三、8大于2和3，8和5组成，父节点为13

四、9大于2、3、8，9和13组成，父节点为22

五、计算带权路径长度：结点的带权路径长度为从根结点到该结点之间的路径长度与该结点的权的乘积。

      WPL = 3*2+3*3+2*8+1*9  =  (2+3)*3+8*2+9*1=40

---

#最后说一句#：编写实属不易，我分享我快乐，若喜欢或者对你有帮助记得点赞、关注、打赏或者收藏哦~