R语言实现聚类分析

l  K-均值聚类（K-Means）   十大经典算法

l  K-中心点聚类（K-Medoids）

l  密度聚类（DBSCAN）

l  系谱聚类（HC）

l  期望最大化聚类（EM）   十大经典算法

 

聚类算法	软件包	主要函数
K-means	stats	kmeans()
K-Medoids	cluster	pam()
系谱聚类（HC）	stats	hclust(), cutree(), rect.hclust()
密度聚类（DBSCAN）	fpc	dbscan()
期望最大化聚类（EM）	mclust	Mclust(), clustBIC(), mclust2Dplot(), densityMclust()

 

 

K-means

countries =read.table("birth.txt",head=F)

#K-均值（K-means）聚类   kmeans()  packages: stats

library(stats)

fit_km1 =kmeans(countries[,-1],center=3)

print(fit_km1)

K-means clustering with 3 clusters of sizes22, 20, 26

Cluster means:

    birth     death

1 17.53636 9.918182

2 25.01500 7.890000

3 42.57692 12.703846

 

Clustering vector:

ALGERIA        CONGO     EGYPT         GHANA   IVORY-COAST       MALAGASY

 3              3              3              3              3              3

MOROCCO      TUNISIA     CAMBODIA      CEYLON        CHINA         TAIWAN

3              3              3              3              3              3

HONG-KONG       INDIA    INDONESIA       IRAQ       JAPAN         JORDAN

  2             1              2              2              1              3

KOREA      MALAYSIA     MONGOLIA  PHILLLIPINES          SYRIA       THAILAND

1              2              3              2             2              3

VIETNAM   CANADA    COSTA-RICA    DOMINICAN-R    GUATEMALA       HONDURAS

   2             2              3              2              3              3

MEXICO   NICARAGUA     PANAMA   UNITED-STATES      ARGENTINA        BOLIVIA

3              3              3              2              2              1

BRAZIL       CHILE      COLOMBIA      ECUADOR          PERU        URUGUAY

   3              3              3              3              2              2

VENEZUELA       AUSTRIA     BElGIUM     BRITAIN      BULGARIA CZECHOSLOVAKIA

   3             1              1              1              1              1

DENMARK     FINLAND    E.GERMANY   W.GERMANY      GREECE       HUNGARY

   1             1              1              1              1              1

IRELAND      ITALY    NETHERLANDS     NORWAY        POLAND       PORTUGAL

   2              1              1              1              1              2

ROMANIA       SPAIN      SWEDEN    SWITZERLAND       U.S.S.R.     YUGOSLAVIA

   1              2              1              1              2              2

AUSTRALIA   NEW-ZEALAND

    2             2

Within cluster sum of squares by cluster:

[1]  272.4836 408.2835 1874.2358

 (between_SS / total_SS =  76.4 %)

 

Available components:

 

[1] "cluster"      "centers"      "totss"        "withinss"     "tot.withinss""betweenss"  

[7] "size"         "iter"         "ifault"   

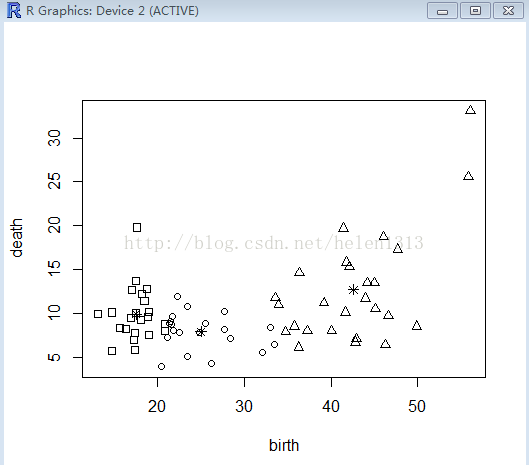
plot(countries[,-1],pch=(fit_km1$cluster-1))

points(fit_km1$centers,pch=8)

kmeans(x, centers, iter.max = 10, nstart = 1,algorithm= c("Hartigan-Wong", "Lloyd", "Forgy","MacQueen"))

 

x: 数据集

centers: 类别数k

iner.max: 迭代最大值，默认10

nstart： 选择随机起始中心点的次数，默认1

algorithm： 4种算法，默认Hartigan-Wong

 

         从上述结果可以看到，数据被分为3类，每类有22, 20, 26个数据；结果给出了各类别的组内平法和，分别为272.4836，408.2835，1874.2358，说明第一类样本点差异最小，第三类差异最大；另外给出了组间平方和占总平方和的76.4%，这个值越大表明组内差距越小，组间差距越大，即聚类效果越好该值可用于与类别数取不同值时的聚类结果进行比较。

 

将center取值从1到67（一共68个样本），选出最优center值：

#K-means聚类_遍历

#一共有68个样本，类别数从1至67取遍

result = rep(0,67)

for(k in 1:67)

         {

         fit_km=kmeans(countries[,-1],center = k)

         result[k]=fit_km$betweenss/fit_km$totss

         }

round(result,2)

 

plot(1:67,result,type="b",main="Choosingthe Optimal Number of Cluster",

xlab="number ofcluster: 1 to 67",ylab="between/totss")

 

K=10的样子，差不多，如果精度要求不是特别高，k-=5,6都可以，按需取值即可。

 

 

K-中心（K-Medoids）

#K-中心点（K-Medoids）聚类  pam(),packages:cluster

library(cluster)

fit_pam =pam(countries[,-1],3)

print(fit_pam)

plot(countries[,-1],pch=(fit_pam$cluster-1))

points(fit_pam$centers,pch=8)

系谱聚类

         先用dist()函数中默认的欧氏距离来生成Countries数据集的距离矩阵，再使用hclust()函数展开系谱聚类。

#系谱聚类

fit_hc =hclust(dist(countries[,-1]))

print(fit_hc)

plot(fit_hc)

形成了一颗自上往下的树，下面对其进行剪枝：

1）利用K值进行剪枝

group_k3 =cutree(fit_hc,k=3)   #剪枝，输出3类别

group_k3

table(group_k3)

group_k3

1   2   3

27  2 39

2）利用Height值进行剪枝

group_h18 =cutree(fit_hc,h=18) #剪枝，输出Height=18时的结果

group_h18

table(group_h18)

group_h18

 1   2 3   4

10  17  2  39

 

画图，可以将类别框出来，有兴趣可以自己画画看，我这里就不贴图了：

plot(fit_hc)

rect.hclust(fit_hc,k=4,border="green")

rect.hclust(fit_hc,k=3,border="red")

rect.hclust(fit_hc,k=7,which=c(2,6),border="darkgrey")

密度聚类

install.packages("fpc")

library(fpc)

ds1 = dbscan(countries[,-1], eps = 1, MinPts = 5)#半径为1，密度阈值为5

ds2 = dbscan(countries[,-1], eps = 4, MinPts = 5)#半径为4，密度阈值为5

ds3 = dbscan(countries[,-1], eps = 4, MinPts = 2)#半径为4，密度阈值为2

ds4 = dbscan(countries[,-1], eps = 8, MinPts = 2)#半径为8，密度阈值为2

ds1;ds2;ds3;ds4        #输出查看

输出如下：

dbscan Pts=68 MinPts=5 eps=1

       0   1

border  59   3

seed   0   6

total   59  9

         其中，为0的列表示噪声；样本被分为两类，第一类含样本6个，第二类含样本3个。说明半径太小，密度阈值太大，导致大多数点被判为噪声点。

dbscan Pts=68 MinPts=5 eps=4

       0  1   2

border  5   7   1

seed   0  18  37

total   5  25  38

         该例将半径扩大，可以看到噪声仅为5个了，样本被分为4类，所含样本点数分布为7、1、18、37。

dbscan Pts=68 MinPts=2 eps=4

      0   1   2   3

border  3   0  0   0

seed   0  25  2  38

total    3  25  2  38

         该例将密度阈值减小到2，噪声只有3个，样本被分为3类，分别含有样本数25、2、38个。

dbscan Pts=68 MinPts=2 eps=8

      1   2

seed  66  2

total   66  2

         该例，将半径翻倍至8，分为2类，一类66个，一类2个。

 

         由上例可以看出，密度聚类需要取恰当的半径和密度阈值。

         为了使我们在着手设置参数时有所依托，不至于无从下手，可以先考察大多数样本间的距离是在怎样一个范围，再以此距离作为半径参数取值：

#考察半径取值

d = dist(countries[,-1])

max(d);min(d)

[1]49.56259

[1]0.2236068

library(ggplot2)  #为使用cut_interval函数，需先下载

interval =cut_interval(d,30)#对样本间距离进行分段处理，取段数30

table(interval)

interval

[0.224,1.87]  (1.87,3.51] (3.51,5.16]  (5.16,6.8]  (6.8,8.45]  (8.45,10.1]  (10.1,11.7] (11.7,13.4] (13.4,15]

78       156       222      201    151     121      141     100     93

(15,16.7] (16.7,18.3]  (18.3,20]  (20,21.6]  (21.6,23.2] (23.2,24.9]  (24.9,26.5]  (26.5,28.2] (28.2,29.8]

  104    104      89      101      97       101      100       83        75

(29.8,31.5] (31.5,33.1] (33.1,34.8] (34.8,36.4](36.4,38.1] (38.1,39.7] (39.7,41.3]  (41.3,43](43,44.6]

   38       30      12       8        8       12       11      14      13

(44.6,46.3] (46.3,47.9]  (47.9,49.6]

   8          5        2

         可以看到，大多数样本点距离在3.51到5.16之间，因此考虑半径3，4，5。如下，对半径去3、4、5和密度阈值取1~10做双层循环：

#对半径去3、4、5和密度阈值取1~10做双层循环

for(i in 3:5)

         {for (j in 1:10)

                   {ds = dbscan(countries[,-1], eps = i, MinPts = j)

                   print (ds)

                   }

         }

         上述程序会打印出30种结果，一般选择类别数多余2，噪声点不要太多的参数。

期望最大化聚类（EM）

#期望最大化聚类 EM  Mclust()  mclust包

library(mclust)

fit_EM =Mclust(countries[,-1])

summary(fit_EM)

----------------------------------------------------

Gaussian finite mixture model fitted by EMalgorithm

----------------------------------------------------

 

Mclust EVI (diagonal, equal volume, varyingshape) model with 4 components:

 

 log.likelihood n   df      BIC       ICL

   -413.3351  68  16    -894.1822  -904.9786

 

Clustering table:

 1 2  3   4

11  2 36  19

plot(fit_EM)

 

         可以画出BIC图，分类图，概率图以及密度图。