graycomatrix 计算(图像)灰度共生矩阵(CLCM)
matlab函数: graycomatrix()
功 能:创建灰度共生矩阵
Gray-level co-occurrence matrix from an image
图像的灰度共生矩阵
灰度共生矩阵是像素距离和角度的矩阵函数,它通过计算图像中一定距离和一定方向的两点灰度之间的相关性,来反映图像在方向、间隔、变化幅度及快慢上的综合信息。
使用方法:
glcm = graycomatrix(I)
glcms = graycomatrix(I,param1,val1,param2,val2,...)
[glcms,SI] = graycomatrix(...)
描述:
glcms = graycomatrix(I) 产生图像I的灰度共生矩阵GLCM。它是通过计算两灰度值 i,j 在图像 I 中水平相邻的次数而得到的 (你也可以通过调整' Offsets' 参数来指定其它的像素空间关系),GLCM中的每一个元素(i,j)代表灰度 i 与灰度 j 在图像 I 中水平相邻的次数。
graycomatrix()先将图像 I 归一化到指定的灰度级,再计算GLCM;这是因为动态地求取图像的GLCM区间代价过高。如果I是一个二值图像,那么灰度共生矩阵就将图像转换到二值灰度级(黑和白)。如果I是一个灰度图像, 那将转换到8灰度级(默认)。灰度的级数决定了GLCM的大小尺寸,假设灰度级为L,则GLCM的尺寸是L x L。你可以通过设定参数“NumLevels”来指定灰度级数目,还可以通过设置“GrayLimits"参数来设置灰度共生矩阵的转换方式。
下图在一个4x5的图像I中显示了如何求解灰度共生矩阵,以(1,1)点为例,在图像 I 中水平相邻的像素对的灰度值都为1的情况只出现了1次,所以GLCM(1,1)的值是1。,同理,在图像 I 中水平相邻的像素对的灰度值分别为 1和2 的情况出现了2次,所以GLCM(1,2)的值是2。 graycomatrix迭代以上过程,就可以计算出GLCM的所有位置(L^2)的取值。
glcms = graycomatrix(I,param1,val1,param2,val2,...) 返回一个或多个灰度灰度共生矩阵,根据指定的参数对的值。参数可以简写,并且对大小写不敏感。
参数
下面按照字母的顺序列写了参数:
'GrayLimits' 是两个元素的向量[low,high],指明了图像 I 中的灰度值如何线性归一化到灰度级别。低于或等于low的灰度值置成1,大于或等于high的灰度值置成NumLevels。如果其设为[],灰度共生矩阵将使用图像I的最小和最大灰度值分别作为GrayLimits的low和high,即[min(I(:) , max(I(:)))]。
'NumLevels' 一个整数,指定灰度级的数目。例如,如果NumLevels为8,意思就是将图像I的灰度映射到1到8之间,它也决定了灰度共生矩阵的大小。默认值是8。
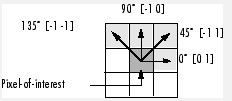
'Offset' 一个p*2的整数矩阵,指定了感兴趣像素对之间的距离和方向。矩阵中的每一行是一个两元素的向量,[row_offset , col_offset],它指定了一对像素之间的关系,或者说是位移。row_offset是感兴趣像素对间隔的行的数目;col_offset是感兴趣像素对间隔的列的数目。offset通常表示一个角度,下面列写的offset的值指定了常见角度。D代表是当前像素与邻居的距离。
Angle Offset
0 [0 D]
45 [-D D]
90 [-D 0]
135 [-D -D]
下图说明了数组:offset = [0 1; -1 1; -1 0; -1 -1]
'Symmetric' 一个布尔型数(逻辑型),指定创建GLCM时像素对中的两像素的顺序是否考虑。例如,当 'Symmetric' 是true时,graycomatrix计算1连接2的次数时,(1,2)和(2,1)这两种数对都计算在内。当'Symmetric'是false时,graycomatrix只是计算(1,2)或(2,1).
[glcm,SI] = graycomatrix(....) 返回归一化(灰度级的)图像,SI,它被用来计算灰度共生矩阵(GLCM),SI图像的取值范围是[1,NumLevels]。
支持类型
I可以是数字型或逻辑型,但必须是二维的,实数的,非稀疏的矩阵。SI是一个double型矩阵,它和I的尺寸相同。glcms是一个‘NumLevels’ x ‘NumLevels’ x P的double型矩阵,P是offsets的数目(即‘Offset’参数值的列数)。
说明:
灰度共生矩阵(GLCM)的另一个名字是灰度空间相关矩阵(gray-level spatial dependence matrix)。另一方面,co-occurrence在文献中使用时经常不带连字符,即cooccurrence。
如果像素对中的一个像素值为NaN,graycomatrix忽略该像素对。
graycomatrix用NumLevels值替代positive Inf,用1代替negative Inf。
如果边界像素的邻居落在图像边界的外边,graycomatrix忽略该边界像素。
当'Symmetric'设置成'true'时,GLCM 是关于对角线对称的,就是Haralick (1973)描述的GLCM。下面句法(1)使用'Symmetric'为'true'时创建了GLCM等于句法(2)和句法(3)使用'Symmetric'为‘false’时产生的GLCM的和。
graycomatrix(I, 'offset', [0 1], 'Symmetric', true) (1)
graycomatrix(I,'offset', [0,1], 'Symmetric', false) (2)
graycomatrix(I,'offset', [0,-1], 'Symmetric',false) (3)
示例:
计算灰度共生矩阵,并且返回缩放后的图像,SI
I = [ 1 1 5 6 8 8; 2 3 5 7 0 2; 0 2 3 5 6 7]; % 生成图像I矩阵
[glcm,SI] = graycomatrix(I,'NumLevels',9,'G',[]) % 计算灰度共生矩阵(glcm)和归一化图像(SI)
计算灰度图像的灰度共生矩阵
I = imread('circuit.tif'); % 读入circuit.tif图像
glcm = graycomatrix(I,'Offset',[2 0]);
参考文献
Haralick, R.M., K. Shanmugan, and I. Dinstein, "Textural Features for Image Classification", IEEE Transactions on Systems, Man, and Cybernetics, Vol. SMC-3, 1973, pp. 610-621.
Haralick, R.M., and L.G. Shapiro. Computer and Robot Vision: Vol. 1, Addison-Wesley, 1992, p. 459.
灰度共生矩阵的特征:
角二阶矩(Angular Second Moment, ASM)
也称为 能量
ASM=sum(p(i,j).^2) p(i,j)指归一化后的灰度共生矩阵
角二阶矩是图像灰度分布均匀程度和纹理粗细的一个度量,当图像纹理绞细致、灰度分布均匀时,能量值较大,反之,较小。
熵(Entropy, ENT)
ENT=sum(p(i,j)*(-ln(p(i,j)))
是描述图像具有的信息量的度量,表明图像的复杂程序,当复杂程序高时,熵值较大,反之则较小。
反差分矩阵(Inverse Differential Moment, IDM)
IDM=sum(p(i,j)/(1+(i-j)^2))
反映了纹理的清晰程度和规则程度,纹理清晰、规律性较强、易于描述的,值较大;杂乱无章的,难于描述的,值较小。
************************************************************************************************************************************************************************
************************************************************* graycomatrix源程序代码 *****************************************************************************
************************************************************************************************************************************************************************
function [GLCMS,SI] = graycomatrix(varargin)
%GRAYCOMATRIX Create gray-level co-occurrence matrix.
% GLCMS = GRAYCOMATRIX(I) analyzes pairs of horizontally adjacent pixels
% in a scaled version of I. If I is a binary image, it is scaled to 2
% levels. If I is an intensity image, it is scaled to 8 levels. In this
% case, there are 8 x 8 = 64 possible ordered combinations of values for
% each pixel pair. GRAYCOMATRIX accumulates the total occurrence of each
% such combination, producing a 8-by-8 output array, GLCMS. The row and
% column subscripts in GLCMS correspond respectively to the first and
% second (scaled) pixel-pair values.
%
% GLCMS = GRAYCOMATRIX(I,PARAM1,VALUE1,PARAM2,VALUE2,...) returns one or
% more gray-level co-occurrence matrices, depending on the values of the
% optional parameter/value pairs. Parameter names can be abbreviated, and
% case does not matter.
%
% Parameters include:
%
% 'Offset' A p-by-2 array of offsets specifying the distance
% between the pixel-of-interest and its neighbor. Each
% row in the array is a two-element vector,
% [ROW_OFFSET COL_OFFSET], that specifies the
% relationship, or 'Offset', between a pair of pixels.
% ROW_OFFSET is the number of rows between the
% pixel-of-interest and its neighbor. COL_OFFSET is the
% number of columns between the pixel-of-interest and
% its neighbor. For example, if you want the number of
% occurrences where the pixel of interest is one pixel
% to the left of its neighbor, then
% [ROW_OFFSET COL_OFFSET] is [0 1].
%
% Because this offset is often expressed as an angle,
% the following table lists the offset values that
% specify common angles, given the pixel distance D.
%
% Angle OFFSET
% ----- ------
% 0 [0 D]
% 45 [-D D]
% 90 [-D 0]
% 135 [-D -D]
%
% ROW_OFFSET and COL_OFFSET must be integers.
%
% Default: [0 1]
%
% 'NumLevels' An integer specifying the number of gray levels to use when
% scaling the grayscale values in I. For example, if
% 'NumLevels' is 8, GRAYCOMATRIX scales the values in I so
% they are integers between 1 and 8. The number of gray levels
% determines the size of the gray-level co-occurrence matrix
% (GLCM).
%
% 'NumLevels' must be an integer. 'NumLevels' must be 2 if I
% is logical.
%
% Default: 8 for numeric
% 2 for logical
%
% 'GrayLimits' A two-element vector, [LOW HIGH], that specifies how
% the grayscale values in I are linearly scaled into
% gray levels. Grayscale values less than or equal to
% LOW are scaled to 1. Grayscale values greater than or
% equal to HIGH are scaled to HIGH. If 'GrayLimits' is
% set to [], GRAYCOMATRIX uses the minimum and maximum
% grayscale values in I as limits,
% [min(I(:)) max(I(:))].
%
% Default: the LOW and HIGH values specified by the
% class, e.g., [LOW HIGH] is [0 1] if I is double and
% [-32768 32767] if I is int16.
%
% 'Symmetric' A Boolean that creates a GLCM where the ordering of
% values in the pixel pairs is not considered. For
% example, when calculating the number of times the
% value 1 is adjacent to the value 2, GRAYCOMATRIX
% counts both 1,2 and 2,1 pairings, if 'Symmetric' is
% set to true. When 'Symmetric' is set to false,
% GRAYCOMATRIX only counts 1,2 or 2,1, depending on the
% value of 'offset'. The GLCM created in this way is
% symmetric across its diagonal, and is equivalent to
% the GLCM described by Haralick (1973).
%
% The GLCM produced by the following syntax,
%
% graycomatrix(I, 'offset', [0 1], 'Symmetric', true)
%
% is equivalent to the sum of the two GLCMs produced by
% these statements.
%
% graycomatrix(I, 'offset', [0 1], 'Symmetric', false)
% graycomatrix(I, 'offset', [0 -1], 'Symmetric', false)
%
% Default: false
%
%
% [GLCMS,SI] = GRAYCOMATRIX(...) returns the scaled image used to
% calculate GLCM. The values in SI are between 1 and 'NumLevels'.
%
% Class Support
% -------------
% I can be numeric or logical. I must be 2D, real, and nonsparse. SI is
% a double matrix having the same size as I. GLCMS is an
% 'NumLevels'-by-'NumLevels'-by-P double array where P is the number of
% offsets in OFFSET.
%
% Notes
% -----
% Another name for a gray-level co-occurrence matrix is a gray-level
% spatial dependence matrix.
%
% GRAYCOMATRIX ignores pixels pairs if either of their values is NaN. It
% also replaces Inf with the value 'NumLevels' and -Inf with the value 1.
%
% GRAYCOMATRIX ignores border pixels, if the corresponding neighbors
% defined by 'Offset' fall outside the image boundaries.
%
% References
% ----------
% Haralick, R.M., K. Shanmugan, and I. Dinstein, "Textural Features for
% Image Classification", IEEE Transactions on Systems, Man, and
% Cybernetics, Vol. SMC-3, 1973, pp. 610-621.
%
% Haralick, R.M., and L.G. Shapiro. Computer and Robot Vision: Vol. 1,
% Addison-Wesley, 1992, p. 459.
%
% Example 1
% ---------
% Calculate the gray-level co-occurrence matrix (GLCM) and return the
% scaled version of the image, SI, used by GRAYCOMATRIX to generate the
% GLCM.
%
% I = [1 1 5 6 8 8;2 3 5 7 0 2; 0 2 3 5 6 7];
% [GLCMS,SI] = graycomatrix(I,'NumLevels',9,'G',[])
%
% Example 2
% ---------
% Calculate the gray-level co-occurrence matrix for a grayscale image.
%
% I = imread('circuit.tif');
% GLCMS = graycomatrix(I,'Offset',[2 0])
%
% Example 3
% ---------
% Calculate gray-level co-occurrences matrices for a grayscale image
% using four different offsets.
%
% I = imread('cell.tif');
% offsets = [0 1;-1 1;-1 0;-1 -1];
% [GLCMS,SI] = graycomatrix(I,'Of',offsets);
%
% Example 4
% ---------
% Calculate the symmetric gray-level co-occurrence matrix (the Haralick
% definition) for a grayscale image.
%
% I = imread('circuit.tif');
% GLCMS = graycomatrix(I,'Offset',[2 0],'Symmetric', true)
%
% See also GRAYCOPROPS.
% Copyright 1993-2008 The MathWorks, Inc.
% $Revision.1 $ $Date: 2008/04/03 03:10:53 $
[I, Offset, NL, GL, makeSymmetric] = ParseInputs(varargin{:});
% Scale I so that it contains integers between 1 and NL.
if GL(2) == GL(1)
SI = ones(size(I));
else
slope = (NL-1) / (GL(2) - GL(1));
intercept = 1 - (slope*(GL(1)));
SI = round(imlincomb(slope,I,intercept,'double'));
end
% Clip values if user had a value that is outside of the range, e.g.,
% double image = [0 .5 2;0 1 1]; 2 is outside of [0,1]. The order of the
% following lines matters in the event that NL = 0.
SI(SI > NL) = NL;
SI(SI < 1) = 1;
numOffsets = size(Offset,1);
if NL ~= 0
% Create vectors of row and column subscripts for every pixel and its
% neighbor.
s = size(I);
[r,c] = meshgrid(1:s(1),1:s(2));
r = r(:);
c = c(:);
% Compute GLCMS
GLCMS = zeros(NL,NL,numOffsets);
for k = 1 : numOffsets
GLCMS(:,:,k) = computeGLCM(r,c,Offset(k,:),SI,NL);
if makeSymmetric
% Reflect glcm across the diagonal
glcmTranspose = GLCMS(:,:,k).';
GLCMS(:,:,k) = GLCMS(:,:,k) + glcmTranspose;
end
end
else
GLCMS = zeros(0,0,numOffsets);
end
%-----------------------------------------------------------------------------
function oneGLCM = computeGLCM(r,c,offset,si,nl)
% computes GLCM given one Offset
r2 = r + offset(1);
c2 = c + offset(2);
[nRow nCol] = size(si);
% Determine locations where subscripts outside the image boundary
outsideBounds = find(c2 < 1 | c2 > nCol | r2 < 1 | r2 > nRow);
% Create vector containing si(r1,c1)
v1 = shiftdim(si,1);
v1 = v1(:);
v1(outsideBounds) = [];
% Create vector containing si(r2,c2). Not using sub2ind for performance
% reasons
r2(outsideBounds) = []; %#ok
c2(outsideBounds) = []; %#ok
Index = r2 + (c2 - 1)*nRow;
v2 = si(Index);
% Remove pixel and its neighbor if their value is NaN.
bad = isnan(v1) | isnan(v2);
if any(bad)
wid = sprintf('Images:%s:scaledImageContainsNan',mfilename);
warning(wid, ...
'GLCM does not count pixel pairs if either of their values is NaN.');
end
Ind = [v1 v2];
Ind(bad,:) = [];
if isempty(Ind)
oneGLCM = zeros(nl);
else
% Tabulate the occurrences of pixel pairs having v1 and v2.
oneGLCM = accumarray(Ind, 1, [nl nl]);
end
%-----------------------------------------------------------------------------
function [I, offset, nl, gl, sym] = ParseInputs(varargin)
iptchecknargin(1,9,nargin,mfilename);
% Check I
I = varargin{1};
iptcheckinput(I,{'logical','numeric'},{'2d','real','nonsparse'}, ...
mfilename,'I',1);
% Assign Defaults
offset = [0 1];
if islogical(I)
nl = 2;
else
nl = 8;
end
gl = getrangefromclass(I);
sym = false;
% Parse Input Arguments
if nargin ~= 1
paramStrings = {'Offset','NumLevels','GrayLimits','Symmetric'};
for k = 2:2:nargin
param = lower(varargin{k});
inputStr = iptcheckstrs(param, paramStrings, mfilename, 'PARAM', k);
idx = k + 1; %Advance index to the VALUE portion of the input.
if idx > nargin
eid = sprintf('Images:%s:missingParameterValue', mfilename);
error(eid,'Parameter ''%s'' must be followed by a value.', inputStr);
end
switch (inputStr)
case 'Offset'
offset = varargin{idx};
iptcheckinput(offset,{'logical','numeric'},...
{'2d','nonempty','integer','real'},...
mfilename, 'OFFSET', idx);
if size(offset,2) ~= 2
eid = sprintf('Images:%s:invalidOffsetSize',mfilename);
error(eid, 'OFFSET must be an N-by-2 array.');
end
offset = double(offset);
case 'NumLevels'
nl = varargin{idx};
iptcheckinput(nl,{'logical','numeric'},...
{'real','integer','nonnegative','nonempty','nonsparse'},...
mfilename, 'NL', idx);
if numel(nl) > 1
eid = sprintf('Images:%s:invalidNumLevels',mfilename);
error(eid, 'NL cannot contain more than one element.');
elseif islogical(I) && nl ~= 2
eid = sprintf('Images:%s:invalidNumLevelsForBinary',mfilename);
error(eid, 'NL must be two for a binary image.');
end
nl = double(nl);
case 'GrayLimits'
gl = varargin{idx};
iptcheckinput(gl,{'logical','numeric'},{'vector','real'},...
mfilename, 'GL', idx);
if isempty(gl)
gl = [min(I(:)) max(I(:))];
elseif numel(gl) ~= 2
eid = sprintf('Images:%s:invalidGrayLimitsSize',mfilename);
error(eid, 'GL must be a two-element vector.');
end
gl = double(gl);
case 'Symmetric'
sym = varargin{idx};
iptcheckinput(sym,{'logical'}, {'scalar'}, mfilename, 'Symmetric', idx);
end
end
end