有限元分析的基本知识 (一份培训资料) (2)

二 有限元分析的基本过程
1 单元
有限元 - 连续体的离散化，将整体结构分割为若干基本单元，每个单元有若干节点。单元中的基本物理量 (结构分析 - 位移；热分析 - 温度；电磁分析 - 电位势，磁通量；流体分析 - 流量，等) 用单元节点处的值表示，可以写为：
{u} = [P] {ue}
其中：
{u} - 单元中任意点的物理量值，它是坐标的函数：
{u} = {u (x,y,z)}
[P] - 形状函数，与单元形状、节点坐标和节点自由度等有关
{ue} - 单元节点的物理量值；对于结构位移法可以是位移、转
角或其对坐标的导数。
常用的大型分析软件中基本上是位移+转角。
结构分析时一些常用单元的节点自由度 (在单元坐标系中)
杆元：单元形状为线段，变形形式为拉伸和扭转。
在单元坐标系中：
节点自由度为 Tx 和 Rx，其中 x 为杆的轴线。
在总体坐标系中：
三个位移和三个转角 (T1,T2,T3,R1,R2,R3)。
梁元：单元形状为线段，变形形式为拉伸、扭转，以及两个垂
直于轴线方向的弯曲
在单元坐标系中：
节点自由度为 Tx,Ty,Tz,Rx,Ry,Rz。其中 x 为梁的
轴线，Y,z 为梁截面的两个抗弯惯矩主轴方向。
在总体坐标系中：
三个位移和三个转角 (T1,T2,T3,R1,R2,R3)。
平面单元：三角形或四边形，变形为两个面内位移。
节点自由度为 T1,T2。单元坐标系与总体坐标系一致。
轴对称单元：三角形或四边形，变形为两个面内位移。
节点自由度为 T1,T2。单元坐标系与总体坐标系一致。
板壳元：三角形或四边形，变形包括两个面内位移，法向位移
及两个转角 (一般缺少绕法线转角)。
在单元坐标系中：
三个位移和三个转角 (Tx,Ty,Tz,Rx,Ry)
在总体坐标系中：
三个位移和三个转角 (T1,T2,T3,R1,R2,R3)
三维实体：四面体～六面体，三个方向的位移，无转角。
节点自由度为三个位移 (T1,T2,T3)，单元坐标系与总
体坐标系一致。

结构分析时一些特殊单元
为了表征结构分析中遇到的一些特殊现象，多数 CAE 软件中都引入了一些特殊的单元，例如：
弹簧单元 - 模拟拉压或弯扭弹簧连接
阻尼单元 - 模拟阻尼器等结构件
质量单元 - 用于处理集中质量
接触单元 - 用于处理接触非线性问题
间隙单元 - 用于处理接触非线性问题
拉索单元 - 用于模拟只受拉不受压的线结构
各种连接单元 - 用于模拟结构件之间的不同连接方式，如
铰接、刚性连接等
刚体单元 - 将结构的某一部分处理为刚体，可减小计算模
型的规模
等

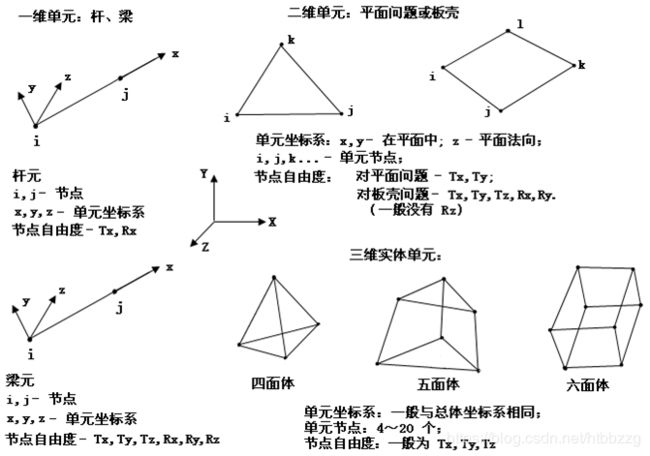
单元形状函数举例 (未必是实际使用的单元)：
(1) 一维单元
a. 杆单元
轴向拉伸和扭转：节点位移自由度为 Tx，Rx
对 2 节点单元 (线性单元)：
Tx = a0 + a1 * x
Rx = b0 + b1 * x
各有 2 个未知数，可以由 2 个节点的位移值确定；
对 3 节点单元 (二次单元)：
Tx = a0 + a1 * x + a2 * x2
Rx = b0 + b1 * x + b2 * x2
各有 3 个未知数，可以由 3 个节点的位移值确定；

b. 梁单元
拉伸和扭转的形状函数与杆的情况相同；
对于弯曲变形 (以单元坐标系 y 向为例)，2 节点单元相应的形状函数为：
Ty = c0 + c1x +c2x2 + c3x3
由两个节点的 Ty,Rz 可以确定四个未知数；
对于 3 节点单元：
Ty = c0 + c1x +c2x2 + c3x3 +c4x4 + c5x5
由 3 个节点的 Ty,Rz 可以确定 6 个未知数；

(2) 二维单元
a. 平面单元 (平面问题，轴对称问题) ，以 Tx 为例
三节点三角元：
Tx = a0 + a1x + a2y
三个未知数可以由三个节点的 Tx 表示；
6 节点三角元：
Tx = a0 + a1x + a2y + a3x2 + a4xy + a5y2
6 个未知数可以由 6 个节点的 Tx 表示；
4 节点四边形元：
Tx = a0 + a1x + a2y + a3xy
4 个未知数可以由 4 个节点的 Tx 表示；
8 节点四边形元：
Tx = a0 + a1x + a2y + a3x2 + a4xy + a5y2
+ a6(x3 + xy2) + a7*(x2y + y3)
8 个未知数可以由 8 个节点的 Tx 表示；

上面使用的简单多项式，对于 4 节点或 8 节点四边形 (特别是使用简单多项式的 8 节点单元，三次项缺失较多)，使用效果往往不好。
实际使用的是 “等参数单元”，通过曲线坐标变换，将任意三角形或四边形变换为等参数坐标系中的正三角形或正方形。然后用 “内插函数” 来构造形状函数。

(2) 二维单元 (续)
b. 弯曲单元 (板、壳问题)
平面内的变形与平面问题相同，主要考虑法向弯曲变形 - Tz，每个节点有三个弯曲自由度：Tz, Rx, Ry (法向位移和两个转角)。
三节点三角元：
Tz = a0 + a1x + a2y + a3x2 + a4xy + a5y2
+ a6x3 + a7*(x2y + xy2) + a8y3
9 个未知数可以由三个节点的 Tz, Rx, Ry 表示。
这是一个不完整的三次多项式，实际使用的是完整的三次多项式，然后添加约束条件消除多出来的一个未知数。
4 节点四边形元：
Tz = a0 + a1x + a2y + a3x2 + a4xy + a5y2
+ a6x3 + a7x2y + a8xy2 + a9y3 + 2 个四次项
12 个未知数可以由四个节点的 Tz, Rx, Ry 表示。这是一个不完整的四次多项式，效果较差，实际使用的是 “等参数单元”。
同样可以构造 “高阶” 单元 (6 节点三角元、8 节点四边形单元)。

(3) 三维实体单元
每个节点三个自由度：Tx,Ty,Tz，一般情况，单元坐标系 x,y,z 与总体坐标系 X,Y,Z 相同。
a. 四面体单元 (以 Tx 为例)
4 节点单元：
Tx = a0 + a1x + a2y + a3z
四个未知数由四个节点的 Tx 确定。
10 节点单元 (增加 6 个边的中点)：
Tx = a0 + a1x + a2y + a3z + a4x2 + a5y2 +
a6z2 + a7xy + a8yz + a9zx
10个未知数由 10 个节点的 Tx 确定。
b. 六面体单元 (以 Tx 为例)
8 节点单元 (直观的例子，实际用 “等参数单元”)：
Tx = a0 + a1x + a2y + a3z + a4x2 + a5y2 +
a6z2 + a7*(xy + yz + zx)
8 个未知数由 8 个节点的 Tx 确定。
20 节点六面体单元：
使用完整的三次多项式，共 20 个未知数，由 20 个节点的 Tx 确定。实际中使用的是 “等参数单元”。
理论上，计算结果应该随着网格的细化而收敛到精确值。但实践发现，单元的形状函数对其计算结果和收敛性有较大影响。经数学界研究发现，单元的构造必须满足相容性 (协调性) 和完备性要求，才能保证计算结果的收敛性。
(1) 单元的完备性要求：
对一般的多项式形式的单元形状函数，必须是与所解决问题的 “应变-位移” 关系式中的最高阶导数相同阶数的完整多项式。
与 “应变-位移” 关系式中的最高阶导数相同阶数的多项式，在 “应变-位移” 关系式中微分后得到常应变项。因此，如果该多项式不完整，就会丢失某些常应变项，导致结果不准确。
这一条可以归结为：位移函数必须包含全部刚体位移和常应变项。

(2) 单元的相容性 (协调性) 要求：
单元的位移函数必须包含所解决问题的 “应变-位移” 关系式中的最高阶导数低一阶的连续性。即，在相邻单元的边界上，该导数必须连续。
如一般弹性问题 (平面问题、轴对称问题和三维弹性问题)，其 “应变-位移” 关系式中只包括位移对坐标的一阶导数，只要求在单元边界上位移连续。因此其位移形状函数只要包含坐标的一次多项式即可 (Tx = a0 + a1x + a2y + a3*z …)。
对板弯曲问题，“应变-位移” 关系式包含位移对坐标的二次导数，在单元边界上需要位移和转角都连续，因而板弯曲单元的节点自由度至少需要三个自由度：Tz,Rx,Ry。这也造成了难以构造简单而又满意的板弯曲单元。
在满足相容性 (协调性) 要求的情况下，随着网格的细化，结果是单调收敛的。如果只满足完备性，而不满足相容性 (如板弯曲问题)，解有时也能收敛，但一般不是单调收敛。

2 单元特性的推导 (略)

3 单元组集
将所有单元的应变能求和，得到整个结构的应变能：
U = S Ue = 1/2 {u}T [K] {u}
其中 {u} 是整个结构所有节点的总体位移自由度按顺序排列所成,称为结构位移矢量；[K] 是将各单元的刚度矩阵对应相同总体自由度的元素叠加后得到。
考虑两个杆单元的情况 (下页图)，各单元的节点位移矢量和单元刚度矩阵用总体自由度序号表示如下：

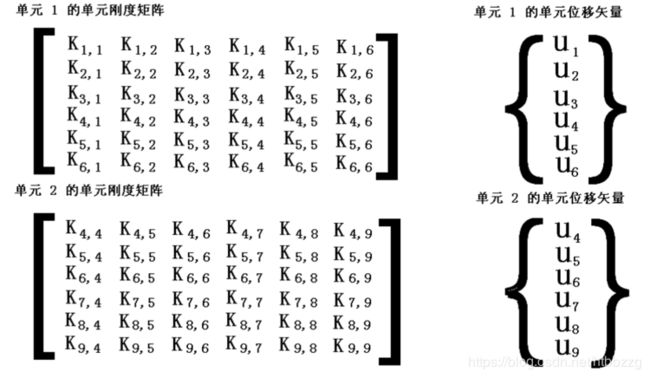
在计算整个结构的应变能时，将两个单元刚度矩阵中具有相同下标的元素进行求和，例如 K4,4 ~ K4,6、K5,4 ~ K5,6、K6,4 ~ K6,6，从而得到整个结构的刚度矩阵。

如果单元中作用有外力，可以根据静力等效原理把它们分配到单元的节点上：

然后可以求出节点外力在节点位移上所做的功：
V = [F] {u}
其中 [F] 为所有节点的外力矢量 (每个节点三个分量)，{u} 为所有节点的位移矢量 (每个节点三个分量)。
然后，根据最小势能原理，真实位移应该使总势能取极小值：
总势能为：
P = U - V = 1/2 {u}T [K] {u} - [F] {u}
对 {u} 取极值，即总势能对 {u} 的一次导数为零：

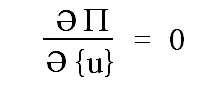
由此得到：
[K] {u} - {F} = 0
或
[K] {u} = {F}
这就是待求解的有限元代数方程。由于将复杂的微分方程转换为有限个数的代数方程，从而使问题的求解变得容易。
不过，现在还不能马上求解，因为数学上已经证明，没有约束的结构的刚度矩阵是一个奇异矩阵 (行列式为零)，从物理上来说，即存在刚体运动，及时很小的外力也能够造成无穷大的位移。为了求解，必须对结构施加足够的约束以消除所有可能的刚体运动。
常用的约束条件有：
指定节点位移 (通常是零)；
弹性约束 (弹性地基)
等。
缺乏足够的约束常常是求解失败的主要原因之一。
在约束自由度上会产生约束反力，对于结构而言，约束反力也是一种外力，以 {R} 表示约束反力，整个结构的方程可以写成：
[K] {u} = {F} + {R}
其中反力 {R} 仅在约束自由度上不为零。
对整个结构的位移自由度重新排序，将已知位移自由度放到最后，分别以下标 f 和 r 代表未知和已知的自由度，则有：

展开后分解为两个方程：
[Kff] {uf} = {Ff}
[Krf] {uf} + [Krr] {ur} = {Fr} + {R}
第一个方程用来求解未知的位移自由度，第二个方程改写为：
{R} = {Fr} - [Krf] {uf} - [Krr] {ur}
用来计算约束反力。
在求出整个结构的节点位移后，可以回到各单元，计算单元的应力、应变等其它所需的物理量 (通常称为数据恢复)。至于节点应力、应变等物理量，通常用与节点相邻的单元的平均值代表。