六自由度(6DoF)弹道在现代外弹道中属于新科贵族。尽管轴对称旋转弹的6DoF刚体弹道模型在20世纪初就已经被建立,但是直到50年代美国 BRL 的 R.H.Kent 才系统性地采用向量方法重新定义了刚体弹道。文中采用弹轴矢量法介绍6DoF刚体弹道只是对 R.H.Kent 等理论的更新和整理。在30年代的 BRL,很多学者就已经对6DoF弹道模型非常了解了,但是还没有出现在实用层面上对这些微分方程进行求解的,直到40年代末期高速数字计算机的出现才开创了新局面。6DoF弹道模型的实用程序是在50年代末才正式出现,因为当时的计算机已经具备了满足需求的内存和求解速度。现今,计算机的快速发展使得普通的弹道学者也能够自己编程求解6DoF刚体弹道。
本文采用弹轴矢量法来介绍6DoF弹道模型,即通过矢量的方向余弦表示弹体的俯仰和偏航,而不是欧拉角。弹轴矢量法的优势如下:
- 坐标系简单:除基准坐标系外,不需要其他坐标系统,也适合大攻角的情况;
- 数学处理方便:在对6DoF方程进行数学处理(线性化、降阶等)时,推导过程更加方便。
6DoF弹道模型需要采用数值积分的方法求解,数值方法可能是弹道模型(旋转弹和非旋转弹)最精确的求解方式了。如前一章中介绍,数值积分需要提供物理参数、气动力、初始和边界条件等。值得注意的是,弹道学者将数值积分称作“GI-GO(Garbage In - Garbage Out)”,如果你输入的参数(气动等)是有问题的,那么得到的结果一定是错误的或者无法完成计算。对弹道的任何分析都需要依靠高质量的输入参数!
6DoF弹道模型的基本方程
弹道模型的基本要素包含坐标系、作用力、运动方程,其中坐标系和作用力已经在第三章进行了介绍,因此章从运动方程开始。
运动基本方程
基于弹轴矢量法的六自由度(6DoF)刚体弹道模型具有求解弹丸飞行过程中线运动和角运动的能力。牛顿定律表明:刚体的动量变化率等于所有外作用力之和,角动量变化率等于所有作用在刚体上的外力矩之和。
[图片上传失败...(image-b98af5-1523542316105)]
[图片上传失败...(image-ae9d98-1523542316105)]
式中,采用矢量的形式表示作用力和力矩的方向,将公式右侧的力和力矩代入即可得到矢量形式的6DoF弹道模型。
弹轴矢量法中将矢量绕质心的角动量分解为两部分:1)沿弹轴x方向的角动量;2)弹轴法向角动量,因此角动量基本方程表示为:
[图片上传失败...(image-6b74d1-1523542316105)])
轴对称的假设能够将旋转弹绕弹轴方向的角动量分量单独提取出来,将横向部分的角速度q、r 统一考虑在弹轴矢量x的导数以内,对H进行变换得到:
[图片上传失败...(image-2b0b3e-1523542316105)])
其中,第一项表示高转速p引起的角动量分量,对上式进行时间求导后得到角动量的变化率,如下所示。
[图片上传失败...(image-7b7361-1523542316105)])
对公式两侧分别进行点乘和叉乘后,将弹轴方向的转速独立出来,得到两组重要的转换关系式。
[图片上传失败...(image-2a6660-1523542316105)]=\frac{I_{x}p}{I_{y}})
[图片上传失败...(image-18f991-1523542316105)]=\frac{d\vec{x}}{dt})
将第三章中的气动力和力矩代入牛顿第二定律即可得到完整形式的6DoF刚体弹道方程。
[图片上传失败...(image-bc6e61-1523542316105)]] + \frac{\rho SdC_{Np\alpha}}{2m}(\frac{I_{y}}{I_{x}})(\vec{h} \cdot \vec{x})(\vec{v} \times \vec{x}) + \vec{g} + \vec{\Lambda})
[图片上传失败...(image-953c3b-1523542316105)]\vec{x} + \frac{\rho vSdC_{M\alpha}}{2I_{y}}(\vec{v} \times \vec{x}) + \frac{\rho Sd^{2}C_{Mp\alpha}}{2I_{x}}(\vec{h} \cdot \vec{x})[\vec{x} \times (\vec{v} \times \vec{x})]+ \frac{\rho vSd^{2}(C_{Mq}+C_{M\dot{\alpha}})}{2I_{y}}(\vec{x} \times \frac{d\vec{x}}{dt}))
刚体弹道中的向量都可以表示为其在基准坐标系OXYZ上的投影分量(用1、2、3下标表示),则将方程写成分量形式,即方程组:
[图片上传失败...(image-3b2e4c-1523542316105)] + \tilde{C}_{Np\alpha} + g_{1} + \Lambda_{1})
[图片上传失败...(image-1dc3b8-1523542316105)] + \tilde{C}_{Np\alpha} + g_{2} + \Lambda_{2})
[图片上传失败...(image-ed861e-1523542316105)] + \tilde{C}_{Np\alpha} + g_{3} + \Lambda_{3})
[图片上传失败...(image-635907-1523542316105)] + [\tilde{C}{Mp\alpha}](v{1}-vx_{1}{\rm{cos}} \alpha_{t}) +\tilde{C}_{Mq})
[图片上传失败...(image-5f83ba-1523542316105)] + [\tilde{C}{Mp\alpha}](v{2}-vx_{2}{\rm{cos}} \alpha_{t}) +\tilde{C}_{Mq})
[图片上传失败...(image-ccd8f9-1523542316105)] + [\tilde{C}{Mp\alpha}](v{3}-vx_{3}{\rm{cos}} \alpha_{t}) +\tilde{C}_{Mq})
式中,弹体总攻角满足关系式
[图片上传失败...(image-8def46-1523542316105)]
姿态的提取
6DoF弹道模型的基本方程中并不直接对姿态进行求解,需要经过一些处理间接计算。
将弹体滚转角速率提取出来进行独立求解,即公式:
[图片上传失败...(image-c971f8-1523542316105)])
弹轴矢量在基准系中的投影分量,如公式:
[图片上传失败...(image-5a98c4-1523542316105)]
弹轴矢量法直接对速度和角动量进行常微分求解,并不直接得到欧拉角和角速率的关系式,但是采用以下公式可以近似求解飞行过程中的攻角等状态参量。
[图片上传失败...(image-8cd03b-1523542316105)]
[图片上传失败...(image-e9318e-1523542316105)]
[图片上传失败...(image-54f58f-1523542316105)]
[图片上传失败...(image-339a6-1523542316105)] - \psi)
[图片上传失败...(image-57cbb5-1523542316105)]
综上所述,6DoF刚体弹道模型的常微分方程状态量包含质心位移、速率、弹轴矢量和角动量(共12个变量),即
[图片上传失败...(image-6a6297-1523542316105)]
6DoF弹道模型的数值计算
第五章展示了求解常微分方程的四个要素:
- 常微分方程:弹道方程
- 初始条件:射击诸元
- 边界条件:积分时长或弹丸落地
- 数值积分方法:龙格-库塔
除将质点弹道模型替换为6DoF弹道模型外,初始条件也相对更加复杂。6DoF刚体弹道模型中的12个变量均需要赋初值,一般涉及诸元提供的参量仅有滚转角速率一项角运动变量,其他姿态参量既可以直接认为是零值,也可以赋予一个小量,因为这些扰动量最终都会在陀螺稳定作用下衰减。
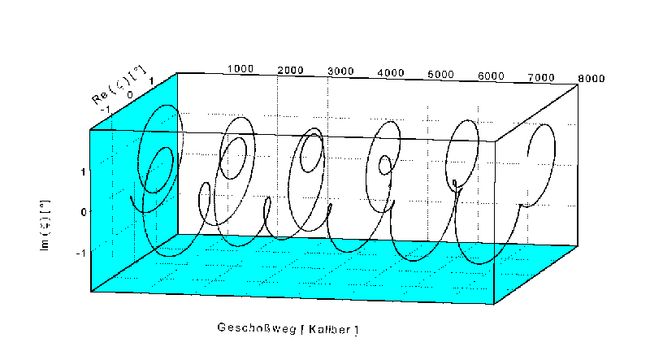
对6DoF弹道模型进行数值积分可以为科学研究提供多样的模拟环境,下面以 BRL 的一组结果展示模型的强大和酷炫,以此开启你的兴趣之门。
后记:至此,《现代外弹道学》系列选译就告一段落了。读过很多本外弹道相关数目,但这本是最朴实的。5年前这本书对我的课题研究进行了启蒙,再次向 R.L.McCoy致以最诚挚的谢意!