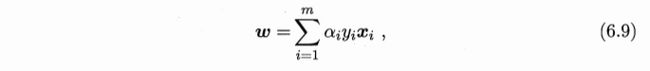将LIBSVM用于多分类时根据svmtrain输出结果得到各OvO分类超平面的法向量w和偏移项b

题目：将LIBSVM用于多分类时根据svmtrain输出结果得到各OvO分类超平面的法向量w和偏移项b

        在前面曾讨论过《由LIBSVM的svmtrain输出结果得到分类超平面的法向量w和偏移项b》（链接https://blog.csdn.net/jbb0523/article/details/80918214），介绍了LIBSVM用于二分类时根据模型返回参数得到超平面方程参数w和b；本篇在此基础上更进一步，讨论将LIBSVM用于多分类时，根据svmtrain输出结果得到分类超平面的法向量w和偏移项b。由于前面已经介绍了有关SVM的基础，因此本篇不讲SVM基础；另外，本篇提及较多的西瓜书式(6.9)位于书中123页6.2节：

        LIBSVM在处理多分类时，采用一对一分解(one vs one, OvO)。有关OvO的细节参见西瓜书的第63页开始的3.5节。对于共有N个类别的多分类问题，OvO分解将其转换为N(N-1)/2个二分类问题，因此这也就共有N(N-1)/2分类超平面。各分类超平面的偏移项(bias)项，也就是b，LIBSVM的模型返回参数直接给出，因此关键在于求出各超平面的法向量w。在《由LIBSVM的svmtrain输出结果得到分类超平面的法向量w和偏移项b》的基础上，不难知道，w可以根据西瓜书式(6.9)求得，而根据式(6.9)求解w的关键在于找出每个x_i对应的alpha_i和y_i。由于多分类时包含N(N-1)/2二分类问题，因此只要能从LIBSVM的模型返回参数中分别找出哪些结果对应哪个OvO二分类问题即可。

        接下来，首先给出MATLAB代码，然后给予适当的解释。程序在Matlab R2014a和LIBSVM最新版(v3.24)上测试通过。

%libsvm用于多分类时的中间参数探索@20191130
clear all;close all;clc;
%% 产生多分类数据集(nr_class = 4)
num_examples = 1000;%生成1000个样本
%控制随机数生成,保证每次产生的数据集相同
%旧版本Matlab的rand('seed', 0)等价于新版本Matlab的rng(0,'v4')
%旧版本Matlab的rand('state', 0)等价于新版本Matlab的rng(0,'v5uniform')
%本版本程序在MATLAB R2014a编写,同时支持两种写法,但诸如Matlab R2009b仅支持旧版本写法
rand('state', 0);%rng(0,'v5uniform');
x = rand(num_examples,2);
y = zeros(num_examples,1);
for ii=1:num_examples
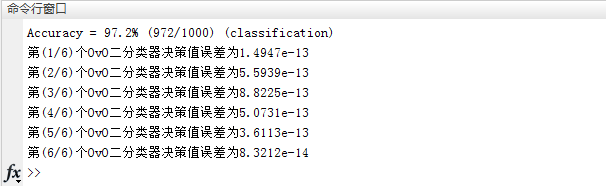
    cond1 = (x(ii,1)

        运行该程序之后，Matlab命令行窗口(Command Window)输出以下结果：

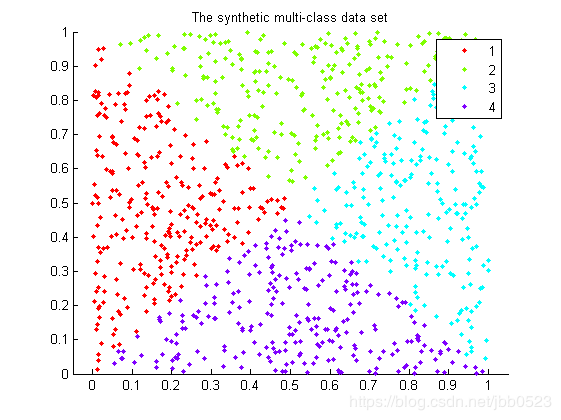
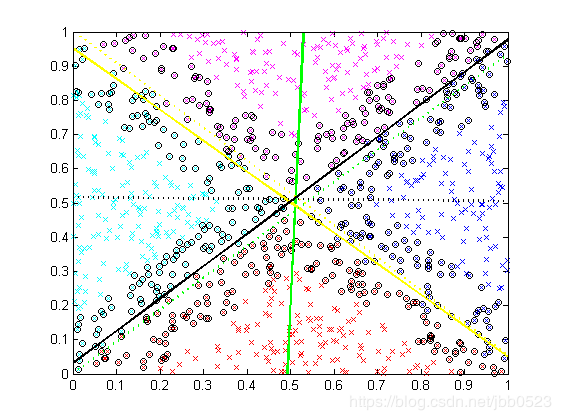
这说明根据计算出来的w和b得到的决策值与svmpredict输出的决策值相同，也就是说计算出来的w和b是正确的。另外还有以下两张图，第1张图是生成的数据集类别分布，第2张图则进一步将标出了支持向量，并画出了所有6个分类平面：

        LIBSVM中svmtrain返回值的解释在《由LIBSVM的svmtrain输出结果得到分类超平面的法向量w和偏移项b》中已经针对二分类问题解释过，另外还可以参考以下两篇博客：

        《libsvm中svmtrain的参数和返回值》(https://blog.csdn.net/Cheese_pop/article/details/61200530)

        《SVM多分类问题 libsvm在matlab中的应用》(https://www.cnblogs.com/litthorse/p/9303711.html)

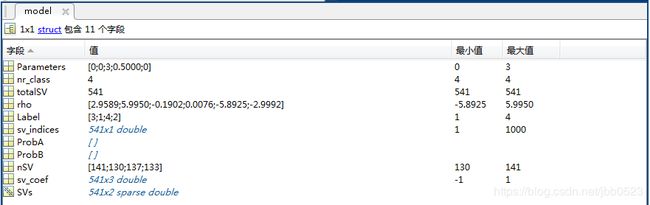
        以下是代码运行之后svmtrain函数的返回值model结构体的明细：

        其中：(1)nr_class是类别个数，当前构建的数据集类别个数为4；

        (2)rho就是偏移项(bias)(i.e., b)的相反数，这里rho共包含6个值，因为4个类别共可以OvO分解为4*(4-1)/2=6个二分类问题；

        (3)sv_indices为所有支持向量的索引，totalSV为支持向量个数，nSV为每个类别的支持向量个数；

        (4)Label为训练样本中类别的符号，这里有一点特别关键：在构建数据集时，程序中使用数字1、2、3、4表示四个类别标记，但这里Label=[3;1;4;2]，这表示在LIBSVM训练时，数字3对应第1个类别，数字1对应第2个类别，数字4对应第3个类别，数字2对应第4个类别，这个顺序很关键，对应接下来提到的第1类(class1)到第4类(class4)；

        (5)sv_coef表示每个支持向量在决策函数中的系数，即西瓜书式(6.9)中的alpha_i*y_i；另外，sv_coef为541*3的矩阵，行数541显然对就支持向量个数，列数3则对应于类别个数减1，也就是每个类别的样本参与构建OvO二分类器的次数；我们可以将sv_coef按对应支持向量的类别分为nr_class=4组（每个类别包含的支持向量个数参见nSV），示意图如下：

        值得注意的是，将sv_coef按上图类拆成的四组的结果，实际上并不是说第1类的第1列141个系数和第2类的第1列的130个系数对应的总共271个样本都是OvO二分类器(class1,class2)的支持向量，你会发现这些系数有好多数值等于0，这是因为每个类别的样本都参与了三个(即类别个数减1)OvO二分类器的构建，该样本可能仅在构建某一个分类器时为支持向量（三列之中该行仅有一个值不为零），也可能在构建某两个分类器时为支持向量（三列之中该行仅有两个值不为零），当然也可能在构建三个分类器时均为支持向量（三列之中该行均不为零）；当然，如果该系数为0，这并不影响根据式(6.9)求解w，因为alpha_i*y_i=0则该样本在式(6.9)中不起作用。

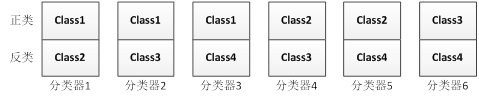
        也就是说，OvO拆解过程是按如下方式依次作为正类和反类的：

        以上正类和反类的安排还可以由sv_coef（即alpha_i*y_i）的符号佐证。由于alpha_i*y_i中的alpha_i≥0，而在SVM中样本为正类时y_i=+1，样本为反类时y_i=-1；因此sv_coef的符号表示了样本为正类还是反类。观察可以发现，第1类的sv_coeff都大于等于零，即在它参与构建的三个OvO分类器中均扮演正类角色；第2类的sv_coeff第1列小于等于零，其余两列都大于等于零，即在它参与构建的第一个OvO分类器中扮演反类角色，在其余两个OvO分类器中扮演正类角色；第3类的sv_coeff第1列和第2列都小于等于零，第3列大于等于零，即在它参与构建的第一个和第二个OvO分类器中扮演反类角色，在第三个OvO分类器中扮演正类角色；第4类的sv_coeff都小于等于零，即在它参与构建的三个OvO分类器中均扮演反类角色。

        了解了sv_coef的存储方式之后，直接结合程序注释就可以看明白程序了。

        最后，注意到程序中svmtrain的参数设置为'-t 0 -q'，即使用的线性核；若使用默认的高斯核，则无法显式地计算出w；这是因为w与特征x的维度相同，高斯核相当于将x映射到了无穷维的空间之中，w也是无穷维的，这时求解决策函数值时只能使用西瓜书式(6.12)的第2个等号之后的求和形式计算，不能根据西瓜书式(6.9)显式地先计算出w，再代入西瓜书式(6.12)的第1个等号之后的w^T*x+b计算。西瓜书式(6.12)如下：

        到此为止，针对LIBSVM用于多分类时的模型返回值的探索暂时告一段落。