[Python嗯~机器学习]---用python来说明线性回归和梯度下降
用python来做线性回归
- 首先,在基本的机器学习思路的基础上我们先研究有监督学习
- 有监督学习学习中分为回归和分类
- 我们先研究回归问题
In [1]:
import numpy as np import matplotlib.pyplot as plt
- 使matplotlib能显示中文
In [2]:
import matplotlib matplotlib.rcParams['font.sans-serif'] = ['SimHei'] matplotlib.rcParams['font.family']='sans-serif' matplotlib.rcParams['axes.unicode_minus'] = False
- 加载数据
In [10]:
def loadDataSet(filename): # 定义一个取数据的函数
X = [] # X,Y分别放到两个列表中
Y = []
with open(filename, 'rb') as f:
for idx, line in enumerate(f): # >>>seasons = ['Spring', 'Summer', 'Fall', 'Winter']
line = line.decode('utf-8').strip() # >>> list(enumerate(seasons))
if not line: # [(0, 'Spring'), (1, 'Summer'), (2, 'Fall'), (3, 'Winter')]
continue #如果行是空的,就continue结束掉
eles = line.split() # 不是空的就split(),成两列
if idx == 0:
numFea = len(eles) # 记录有几个feature特征,eles的长度就是特征个数
eles = list(map(float, eles)) # 把元素都编程浮点型,python3需要在map前加list,map()函数接收两个参数,
# 一个是函数,一个是序列,map将传入的函数依次作用到序列的每个元素,
# 并把结果作为新的list返回
X.append(eles[:-1]) # 去掉每一行的最后一个数据,放到X中,从0数到倒数第一个元素左闭右开
Y.append([eles[-1]]) # 把每行的最后一个元素放入Y中
return np.array(X), np.array(Y) # 把 X,Y 转换成ndarray
In [4]:
def h(theta, X):
return np.dot(X, theta)
- 代价函数
In [17]:
def J(theta, X, Y): # Y 是数据集中真是样本的结果
m = len(X)
return np.sum(np.dot((h(theta, X) - Y).T, (h(theta, X) - Y)) / (2 * m))
上式中h(theta, X) - Y).T是1 m的矩阵,h(theta, X) - Y是一个m 1的矩阵,矩阵乘法得出一个1 * 1的平方值
- 梯度下降
我们通过对损失函数求导得到梯度
我们规定一个步长α乘以梯度得到在函数变化最开的方向的一小段距离,用θ减去这一个距离得到一个新的θ不断迭代
- 批量梯度下降(bgd)
In [15]:
def bgd(alpha, maxloop, epsion, X, Y): # 参数是 步长,最大迭代次数, 两次代价函数迭代的差值,样本特征,结果
m, n = X.shape # 样本的行和列分别样本数和特征数
theta = np.zeros((2, 1)) # 本例中是一元线性回归特征的权重是一个2行1列的矩阵,随便初始化一个值
count = 0 # 初始迭代次数为0
converged = False # 是否收敛立一个flag
error = np.inf # 初始化当前代价函数的值,np.inf表示一个无限大的正数,就是正无穷大
errors = [] # 用一个列表来存储每一次代价函数的输出值
thetas = {0:[theta[0, 0]], 1:[theta[1, 0]]} # 记录参数theta更新的列表,初始化两个参数
while count <= maxloop: # 梯度下降就是一个迭代的过程
if(converged):
break
count = count + 1
# 为了同步更新,把每次计算的theta赋给一个临时变量,最后一起更新
# theta0 赋予一个临时变量
temp1 = theta[0, 0] - alpha / m * (h(theta, X) - Y).sum()
# theta1 付给一个临时变量,根据公式用矩阵乘法推导,np.dot(x[:, 1][:, np.newaxis]是得到的x[:, 1]
#是一个vector,shape是m没有第二维,所以我们给他一个第二维都是1的维度
temp2 = theta[1, 0] - alpha / m * (np.dot(X[:, 1][:, np.newaxis].T, (h(theta,X) - Y))).sum()
# 同步更新
theta[0, 0] = temp1
theta[1, 0] = temp2
thetas[0].append(temp1)
thetas[1].append(temp2)
# 用得到的theta算出当前的代价函数值
error = J(theta, X, Y)
errors.append(error)
if(error < epsion):
converged = True
return theta, errors, thetas
- 使用准备好的数据集,实现梯度下降
In [11]:
X, Y = loadDataSet('./data/ex1.txt')
print(X.shape)
print(Y.shape)
(97, 1) (97, 1)
In [12]:
m, n = X.shape X = np.concatenate((np.ones((m, 1)), X), axis = 1) # 第一列都是1
In [13]:
X.shape
Out[13]:
(97, 2)
In [18]:
alpha = 0.02 # 步长 maxloop = 1500 # 最大循环次数 epsilon = 0.01 # 收敛的判断条件 result = bgd(alpha, maxloop, epsilon, X, Y) theta, errors, thetas = result
In [19]:
xCopy = X.copy() xCopy.sort(0) yHat = h(theta, xCopy) # 预测结果
In [21]:
xCopy[:, 1].shape, yHat.shape, theta.shape
Out[21]:
((97,), (97, 1), (2, 1))
- 画回归直线(假设函数)
In [23]:
plt.xlabel(u'城市人口(万)') plt.ylabel(u'利润(万元)') plt.plot(xCopy[:, 1], yHat, color='r') # 第一个参数是特征值,第二个参数是预测值,这样可以画出假设函数直线 plt.scatter(X[:, 1].flatten(), Y.flatten()) # flatten()把矩阵元素转化成数组元素 plt.show()
- 画代价函数图像
In [24]:
plt.xlim(-1, 1600) plt.ylim(4, 20) plt.xlabel(u'迭代次数') plt.ylabel(u'代价函数J') plt.plot(range(len(errors)), errors) plt.show()
In [28]:
theta
Out[28]:
array([[-3.8782013 ],
[ 1.19126758]])
- 画梯度下降过程图
In [31]:
%matplotlib inline
from mpl_toolkits.mplot3d import axes3d
size = 100
theta0Vals = np.linspace(-10, 10, size)
theta1Vals = np.linspace(-2, 4, size)
JVals = np.zeros((size, size))
for i in range(size):
for j in range(size):
col = np.matrix([[theta0Vals[i]], [theta1Vals[j]]])
JVals[i, j] = J(col, X, Y)
theta0Vals, theta1Vals = np.meshgrid(theta0Vals, theta1Vals)
JVals = JVals.T
三维图形
In [32]:
contourSurf = plt.figure()
ax = contourSurf.gca(projection='3d')
ax.plot_surface(theta0Vals, theta1Vals, JVals, rstride=2, cstride=2, alpha=0.3,
cmap=matplotlib.cm.rainbow, linewidth=0, antialiased=False)
ax.plot(theta[0], theta[1], 'rx')
ax.set_xlabel(r'$\theta_0$')
ax.set_ylabel(r'$\theta_1$')
ax.set_zlabel(r'$J(\theta)$')
Out[32]:
Text(0.5,0,'$J(\\theta)$')
等高线图(康托图)
In [37]:
%matplotlib inline plt.figure(figsize=(12,6)) CS = plt.contour(theta0Vals, theta1Vals, JVals, np.logspace(-2,3,30), alpha=.75) # 此处alpha是透明度 plt.clabel(CS, inline=1, fontsize=10) #clabel标注等高线上的代价函数值 # 绘制最优解 plt.plot(theta[0,0], theta[1,0], 'rx', markersize=10, linewidth=3) # rx是红色x标注靶点 # 绘制梯度下降过程 plt.plot(thetas[0][::10], thetas[1][::10], 'rx', markersize=3, linewidth=1) # 每一次theta取值 #plt.plot(thetas[0], thetas[1], 'r-',markersize=3, linewidth=1) # 用线连起来 plt.show()
![[Python嗯~机器学习]---用python来说明线性回归和梯度下降_第1张图片](http://img.e-com-net.com/image/info8/7ec884a63a154704b4a5d14b0d5d197e.jpg)
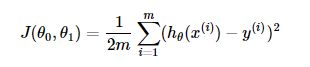
![[Python嗯~机器学习]---用python来说明线性回归和梯度下降_第2张图片](http://img.e-com-net.com/image/info8/7207e1a527234e7cb4158c8eaa619d60.jpg)
![[Python嗯~机器学习]---用python来说明线性回归和梯度下降_第3张图片](http://img.e-com-net.com/image/info8/3d3dc873c8234767a1a8f936dbccf0fc.jpg)
![[Python嗯~机器学习]---用python来说明线性回归和梯度下降_第4张图片](http://img.e-com-net.com/image/info8/9b9a52ee2d0d4f0ea16cd1740a151b46.jpg)
![[Python嗯~机器学习]---用python来说明线性回归和梯度下降_第5张图片](http://img.e-com-net.com/image/info8/f6701bcbb486467898a89e5eca623904.jpg)
![[Python嗯~机器学习]---用python来说明线性回归和梯度下降_第6张图片](http://img.e-com-net.com/image/info8/eced6dc2000d43e6bf5c729c5d47e412.jpg)
![[Python嗯~机器学习]---用python来说明线性回归和梯度下降_第7张图片](http://img.e-com-net.com/image/info8/da2c0c3a263d44d7aa3000758fb73c1e.jpg)