你必须知道的密码基础知识
之前听吴军的《谷歌方法论》讲科技界跟工业界应当在边界内行事-------明确自己所处行业的边界、明确自己所处的各生活关系的界限并在边界处设防,才可规避可预见的风险和意外。对于软件开发者来说也要明确,任何计算机技术也是有边界极限的,我们要认识到其边界极限在哪里,才能更快地看清楚问题的本质。
密码技术
对于密码技术而言,首先我们要认识到密码技术的边界极限在哪里。密码只是信息安全的一部分,它的目的很明确就是为了解决信息安全问题。不同的密码技术算法解决不同的信息安全问题,但没有一种技术能解决所有信息安全问题。
信息安全有四类特性:
- 机密性:为了防止信息被窃听,对应的密码技术有对称密码和非对称密码。
- 完整性:为了防止信息被篡改,对应的密码技术有单向散列函数、消息认证码、数字签名。
- 认证:为了防止攻击者伪装成真正的发送者,对应的密码技术有消息认证码和数字签名。
- 不可否认性:为了防止发送者事后否认自己没有做过,对应的密码技术为数字签名。
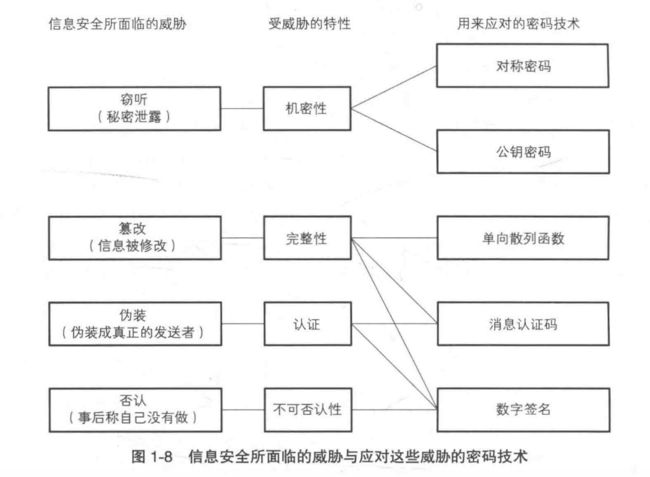
为了尽可能的解决不同的信息安全特性,我们可能需要组合使用多种密码技术。信息安全面临的威胁点和所对应的密码技术之间的关系可用下图来表示:
以上主要从类别分类包括6种密码技术:对称密码、非对称密码、单向散列函数、消息认证码、数字签名、伪随机数生成器。如果看具体的算法,那就包括 AES、RSA、MD5、SHA1、SHA256、HMAC 等。有些人还将 BASE64 也理解为一种加解密的密码技术,但BASE64 只是一种编码方式,和 ASCII 和 UTF-8 编码的本质上一样,主要用途就是将不可打印的二进制数据编码为可打印的字符串,因为它不解决信息安全四个特性中的任何一种。大家都知道高性能和高安全是很难兼顾,鱼和熊掌不可兼得,我们能做的是尽力根据自己的业务找到平衡点。下面分别介绍一下这些技术和他们对应的具体算法。
对称密码
也称为共享密钥密码、私钥密码,是指用相同的密钥加密和解密时的方式。对称加密算法的优点是算法公开、计算量小、加密速度快、加密效率高。缺点是,交易双方都使用同样钥匙,密钥的分发和管理比较困难,安全性得不到保证。
常用的对称加密算法有:DES、3DES、AES、Blowfish、RC5、IDEA 等,其中DES已经可以现实中被暴力破解,现在的使用最广泛的对称加密算法是 AES。
密码算法可以分为分组密码和流密码两种。其中AES和DES都是属于分组密码。分组密码是将明文消息分成一定长度的N个分组,然后对每个分组进行加密。AES的分组长度是128比特, 分组密码有很多模式,如果模式选择不恰当,就无法充分保证机密性。
AES 是一种分组密码,即将明文消息拆分为一定长度的N个分组,然后对每个分组进行加密。AES 的分组长度固定为 128 比特,而密钥可以是 128/192/256比特。既然是固定长度的分组,那我们要加密任意长度的明文,就涉及到如何将多个分组进行迭代加密的问题,因此,就有了分组模式。常用的分组模式有:ECB、CBC、CFB、OFB、CTR 等。最常用的是 ECB 和 CBC 模式,因此,需要了解下这两种模式的用法和区别。
ECB 全称为 Electronic CodeBook,电子密码本模式,是最简单的一种模式,它直接将明文分割成多个分组并逐个加密,如下图: 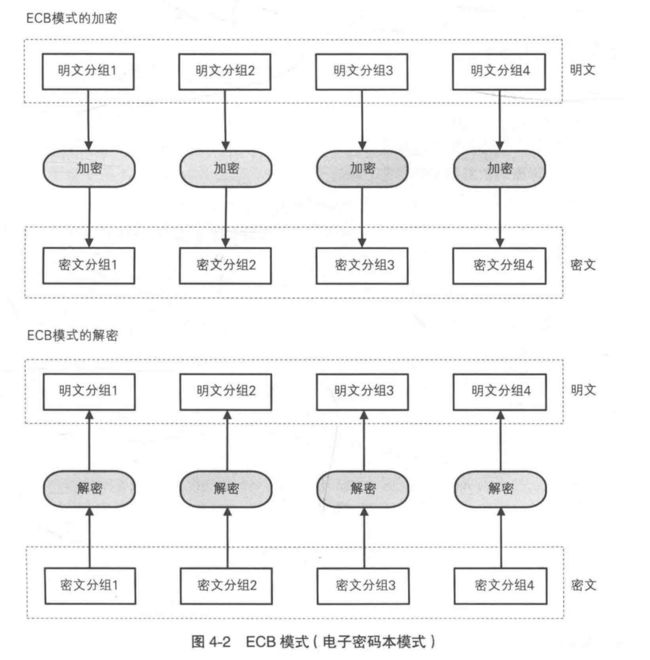
这种模式的优点就是简单、快速,加密和解密都支持并行计算。而缺点也比较明显,因为每个明文分组都各自独立地进行加密和解密,如果明文中存在多个相同的明文分组,则这些分组最终会被转换为相同的密文分组。这样一来,只要观察一下密文,就可以知道明文中存在怎样的重复组合,并可以以此为线索来破译密码。另外,攻击者可以通过改变密文分组的顺序,或删除密文分组,或替换掉密文分组,就可以达到对明文操纵的目的,而无需破译密码。在实际应用中,很少需要进行并行计算的加解密场景,因此,一般情况下不会采用这种分组模式,而更推荐采用 CBC 模式。
CBC 全称为 Cipher Block Channing,密文分组链接模式,是将前一个密文分组与当前明文分组的内容混合起来进行加密的,如下图: 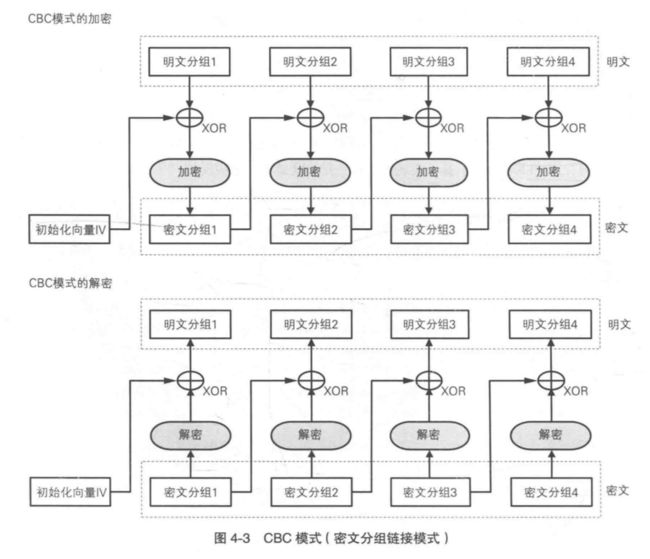
在 CBC 模式中,首先将明文分组与前一个密文分组进行 XOR 运算,然后再进行加密。加密第一个明文分组时,由于不存在“前一个密文分组”,因此需要事先准备一个长度为一个分组的比特序列来代替“前一个密文分组”,这个比特序列称为初始化向量(initialization vector),通常缩写为 IV。CBC 模式避免了 ECB 模式的弱点,明文的重复排列不会反映在密文中。不过,相比 ECB 模式,CBC 模式多了一个初始化向量IV。
另外,当最后一个明文分组的内容小于分组长度时,需要用一些特定的数据进行填充,填充方式也有很多种,常用的有两种:PKCS#5 和 PKCS#7。需要注意的就是,不同编程语言使用的填充方式可能会不同。比如,Java 是使用 PKCS#5,而 iOS 的 Objective-C 和 Swift 则采用 PKCS#7。不过,对于 AES 来说,两种填充方式是一样的。
在实际应用中,我们一般都是在前端对密码或其他敏感数据进行加密,然后在后端进行解密。因为前后端涉及到不同语言的实现,为了保证前后端经过加解密后的结果一致,有几个参数是需要保持一致的:
- 密钥:密钥都要使用同一个,这点基本没有疑问,但需要注意的就是,密钥长度需要统一为 128/192/256 比特,即 16/24/32 字节。
- 分组模式:分组模式推荐统一为 CBC 模式,且要显式声明,因为不同语言的默认分组模式可能会不同。
- 初始化向量:加密和解密时的初始化向量 IV 也是要一致的,同样也不要使用默认设置,而要显式定义。
- 填充方式:Java 采用 PKCS5Padding,iOS 和 JavaScript 采用 PKCS7,对于 AES 来说,两者是一样的。
还有一点也需要注意,AES 算法本身操作的都是 byte 字节数组,因此,加密后一般会使用 BASE64 编码将 byte 数组转为字符串,而解密之前则先用 BASE64 解码将字符串转回 byte 数组。
使用对称加密最关键的就是要保证密钥的安全,一般不建议直接在网络上传输密钥,另外,在客户端也要做好密钥的安全存储。
非对称加密
非对称加密也称公钥加密,使用了一对密钥,用公钥进行加密,再用配对的私钥进行解密。公钥是公开的,而私钥是保密的。相比对称加密安全性提高了,但牺牲了性能,加解密的速度慢了几个数量级,消息越长,加密和解密的速度越慢。
使用最广泛的非对称加密算法就是 RSA,其原理是利用了大整数质因数分解问题的困难度,加密和解密其实就是非常简单的两条公式:
加密:密文 = 明文^E mod N
解密:明文 = 密文^D mod N
即是说,加密就是对明文的 E 次方后除以 N 求余数的过程,其中 E 和 N 的组合就是公钥,即公钥 = (E, N)。而解密过程就是对密文进行 D 次方后除以 N 得到余数,即是明文,D 和 N 的组合就是私钥,即私钥 = (D, N)。公钥和私钥共有的 N 称为 module,即模数,E 和 D 则分别是公钥指数和私钥指数。因为 RSA 是基于以上数学问题的,所以其明文、密钥和密文都是数字,我们平时看到的字符串其实都是二进制表示的数字经过 BASE64 编码的。
密钥长度越长越安全,推荐使用 1024 比特或更大的值,这里说的 1024 密钥长度其实是指模数的长度。还有,不同于对称密码可以加密任意长度的明文,RSA 明文长度是不能超过密钥长度的。Java 默认的 RSA 加密实现明文长度最长为密钥长度减去 11 字节,假如密钥长度设为 1024 比特,即 128 字节,那明文长度则不能超过 128 - 11 = 117 字节,如果超过该长度则会抛异常。如果想要加密的明文比较长,那就生成更长的密钥,如 2048 比特,那明文可以长达 245 字节,足够了。太长的明文也不推荐使用 RSA 进行加密,性能太低了。
另外,为了提高安全性,RSA 加密时都会填充一些随机数。RSA 加密填充方式主要有三种:NoPadding、PKCS1Padding、OAEPPadding。其中,最常用的就是 PKCS1Padding,它会在明文前面填充 11 字节的随机数,因此,对同一明文每次加密产生的密文都会不一样。如果想让每次加密产生的密文都一样,那填充方式就采用 NoPadding,即不填充,但这样无疑减低了安全性,所以一般不建议采用 NoPadding。
实际应用中,我们不会直接对长消息进行非对称加密,而只会对一些安全性要求非常高的短消息进行加密,比如用户的密码、对称加密的密钥。SSL/TLS 的加密方案就是用对称加密对请求消息进行加密,用公钥加密对对称加密的密钥进行加密。
单向散列函数
消息认证码
消息认证码是一种确认完整性并进行认证的技术,英文名称为message authentication code,简称为MAC。
虽然单向散列函数可以用来对消息进行完整性校验,但无法校验消息是否来自合法的发送者,即无法解决认证问题。要解决发送者的认证问题,最常用的有两种方案,一是采用消息认证码,二是使用数字签名。这一小节我们先来了解下消息认证码。
消息认证码的输入包括任意长度的消息和一个发送者与接收者之间共享的密钥,它可以输出固定长度的数据,这个数据称为 MAC 值。
消息认证码的实现方式有很多种,最常用的实现方式就是 HMAC,再具体点,根据使用哪种单向散列函数可分为:HMAC-MD5、HMAC-SHA1、HMAC-SHA256 等等。HMAC 简单理解就是带有密钥的散列函数,因为有了密钥,就可以对发送者进行认证;也因为使用了散列函数,也具有完整性校验的性质。
认证的基本流程就是:
发送者使用共享密钥对消息计算 MAC 值;
发送者将消息和 MAC 值一起发送给接收者;
接收者收到消息和 MAC 值后,使用同一个共享密钥对消息计算 MAC 值;
对比计算出来的 MAC 值和接收到的 MAC 值是否一致,一致则认证成功。
现在,很多接口所添加的 URL 签名机制,其实就是对请求做 MAC 认证,具体的设计细节后面的文章再详细说明。
不过,因为使用了共享密钥,因此也存在和对称加密一样的密钥安全问题。
数字签名
数字签名相当于现实世界中的盖章、签字的功能,使用数字签名可以识别篡改和伪装,还可以防止否认。
数字签名可以解决发送者的认证问题,而且,数字签名还具有不可抵赖性。数字签名的原理也非常简单,其实就是将非对称加密反过来用。我们知道,非对称加密是用公钥加密,然后用私钥解密。而数字签名则是用私钥加密,生成的密文就是数字签名,再用公钥解密。用私钥进行加密这一行为只能由持有私钥的人完成,正是基于这一事实,才可以将用私钥加密的密文作为签名来对待。而由于公钥是对外公开的,因此任何人都可以用公钥进行解密,即任何人都能够对签名进行验证。
另外,我们也知道,非对称加密本身加密和解密是非常慢的,消息越长,性能越慢,因此,一般不用来加密和解密长消息。同样的,一般也不会直接对长消息签名,通常的做法是对消息的散列值进行签名,因为散列值比较短,所以加密签名相对就会快很多。因此,你会看到数字签名有类似 MD5withRSA、SHA1withRSA 这样的实现。
最后,需要注意一点,像 MD5withRSA 和 SHA1withRSA 这样的数字签名实现可以校验消息完整性、对发送者进行认证、还可防止抵赖,但却不能解决机密性的问题,不要妄想用一种密码技术就能解决所有问题。
不过,数字签名其实不太适合直接用在客户端上。因为客户端要对消息签名,那么客户端就需要保存私钥,那依然有私钥的安全配送和存储问题。数字签名使用最广泛的应该就是用在数字证书上了,这还涉及到 SSL/TLS 和 CA 等,后面的文章再聊这个话题。
伪随机数生成器
伪随机数生成器并不直接解决信息安全问题,但它承担了密钥生成的重要职责。而密钥的重要性就不用多说了。
总结
密码技术其实非常多,还包括各种单一技术的组合,我们本篇文章所学的只是最基础的一些知识,包括了对称加密、非对称加密、单向散列函数、消息认证码、数字签名这些密码技术的一些必备知识点,只有掌握了这些,才能理解和设计一些安全性更高的应用。
对称加密和非对称加密用来解决机密性问题,对称加密的速度快,适合用来加密长消息,但密钥在安全配送和客户端的存储是个难点;而非对称加密避免了共享密钥的安全配送和存储问题,但对长消息的加密速度非常慢,只适合用来加密短消息。单向散列函数可以用来对消息进行完整性校验,但很少单独使用。消息认证码简单理解就是带密钥的单向散列函数,既能校验完整性,还能对发送者进行认证,但因为使用了共享密钥,也存在和对称密码一样的共享密钥的安全配送和存储问题。数字签名能解决完整性校验、认证和防止抵赖等问题,最广泛的应用是在数字证书上。
思考和实践
在实际应用中,当进行一些安全性的设计时,如何在以上这些密码技术之间进行选型?如何设计一套安全的 API ?