双边滤波及MATLAB算法实现

双边滤波器的定义

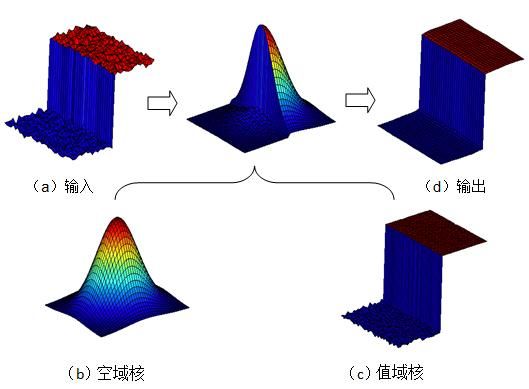
双边滤波器（Bilateral filter）为使图像平滑化的非线性滤波器，它除了使用像素之间几何上的靠近程度之外，还多考虑了像素之间的灰度差异， 使得双边滤波器能够有效的将图像上的噪声去除，同时保存图像上的边缘信息。

双边滤波器的好处是可以做边缘保护（edge preserving），一般用高斯滤波、均值滤波等滤波器去降噪，会较明显地模糊边缘，对于高频细节的保护效果并不明显。双边滤波器顾名思义比高斯滤波多了一个高斯方差sigma-d，它是基于空间分布的高斯滤波函数，所以在边缘附近，离的较远的像素不会太多影响到边缘上的像素值，这样就保证了边缘附近像素值的保存。但是由于保存了过多的高频信息，对于彩色图像里的高频噪声，双边滤波器不能够干净的滤掉，只能够对于低频信息进行较好的滤波。

双边滤波器的原理

空间距离：指的是邻域内某点与中心点的欧式距离。空间域高斯函数其数学形式为（这就是高斯滤波核）：
                                                                             

其中（xi,yi）为邻域内某点位置，（xc,yc）为中心点的位置，sigma为空间域标准差。       

灰度距离：指的是邻域内某点灰度与中心点灰度的差的绝对值。值域高斯函数其数学形式为：
                                                    

其中gray(xi,yi)为邻域内某点灰度值，gray(xc,yc)为中心点灰度值，sigma为值域标准差。

 对于高斯滤波，仅用空间距离的权值系数核与图像卷积后，确定中心点的灰度值。即认为离中心点越近的点，其权重系数越大。双边滤波中加入了对灰度信息的权重，即在邻域内，灰度值越接近中心点灰度值的点的权重更大，灰度值相差大的点权重越小。所以掩膜最终权重大小，则由空间域高斯核函数和值域高斯核函数共同确定。
 

双边滤波器的MATLAB代码实现

bftGrayImage.m文件

function J=bftGrayImage(I,G,sigma_d,sigma_r,filterRadius)
x=-filterRadius:filterRadius;
y=-filterRadius:filterRadius;
J=zeros(size(I));
[xx,yy]=meshgrid(x,y);
spatialCoeffs=exp(- (xx.^2+yy.^2)/(2*sigma_d^2));
[rows,cols]=size(I);
parfor y=filterRadius+1:rows-filterRadius
    for x=filterRadius+1:cols-filterRadius
        roi= I(y-filterRadius:y+filterRadius,x-filterRadius:x+filterRadius);
        centerValue=G(y,x);
        roidif=roi-centerValue;
        tonalWeight =exp(- roidif.^2/(2*sigma_r^2));
        F=(tonalWeight.*spatialCoeffs);
        k=sum(F(:));
        weight=F.*roi;
        J(y,x)=sum(weight(:))/k;
    end
end
J=mat2gray(J);
J=J(filterRadius+1:end-filterRadius,filterRadius+1:end-filterRadius);
end

main.m文件调用：

g = double(imread('../xx图片/IR00040.jpg'))/255.0;
g = rgb2gray(g);
G=g;%guidance image
sigma_d=2;
sigma_r=0.3;
filterSize=double(uint8(3*sigma_d)*2+1);
 
filterRadius=ceil((filterSize-1)/2);
I=padarray(g,[filterRadius,filterRadius],'replicate');
G=padarray(G,[filterRadius,filterRadius],'replicate');
 
J=bftGrayImage(I,G,sigma_d,sigma_r,filterRadius);
 
%figure;imshow([g,J]);title('input,output');
figure;
imshow(g,[]);
title('input');
figure;
imshow(J,[]);
title('output');

σ的意义及选取
1）空间域sigma-d选取：

sigma-d越大，图像越平滑，趋于无穷大时，每个权重都一样，类似均值滤波；

sigma-d越小，中心点权重越大，周围点权重越小，对图像的滤波作用越小，趋于零时，输出等同于原图。

2）值域sigma-r选取：

Sigma-r越大，边缘越模糊，极限情况为simga无穷大，值域系数近似相等（忽略常数时，将近为exp（0）= 1），与高斯模板（空间域模板）相乘后可认为等效于高斯滤波。

Sigma-r越小，边缘越清晰，极限情况为simga无限接近0，值域系数除了中心位置，其他近似为0（接近exp（-∞） =  0），与高斯模板（空间域模板）相乘进行滤波的结果等效于源图像。