javascript 实现 A-star 寻路算法
在游戏开发中,又一个很常见的需求,就是让一角色从A点走到B点,而我们期望所走的路是最短的,最容易想到的就是两点之间直线最短,我们可以通过勾股定理来求出两点之间的距离,但这个情况只能用于两点之间没有障碍物的情况,如果两点之间有很多不可避免无法穿过的障碍物的时候,怎么办呢?因此,我们的需求就是:计算出两点之间的最短路径,而且能够避开所有的障碍物
A-star javascript实现
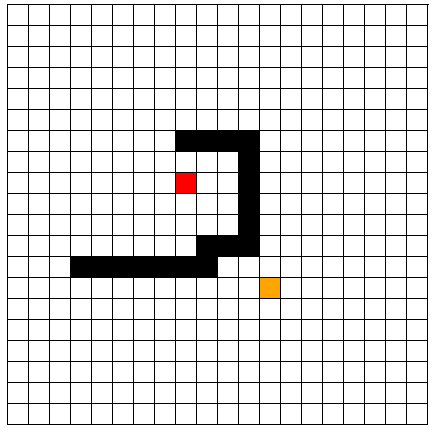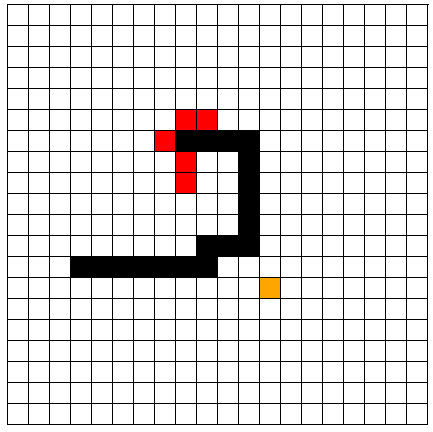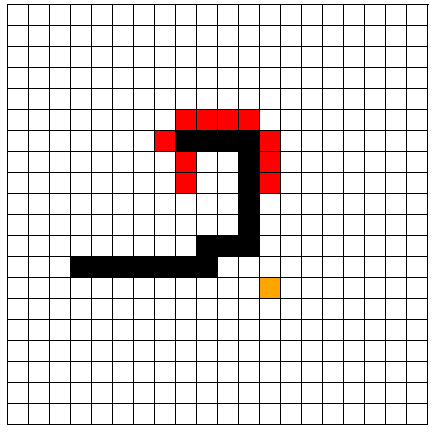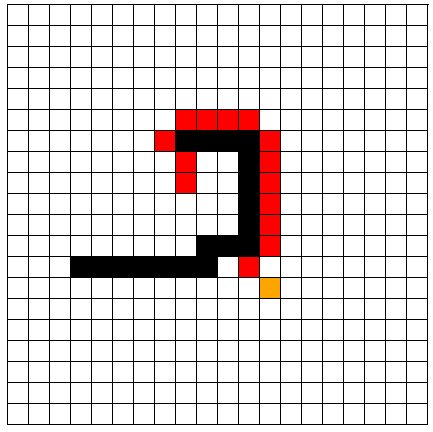
第一种情况:
在这种情况下,所走路径方向朝上
第二种情况:
当我们把上方的障碍物增多的时候,选择走的路径就往下走
第三种情况:
在障碍物中间打开一个口子,那么所选择的路径就会之间从中间穿过
前置知识,百度百科:
启发式搜索:启发式搜索(Heuristically Search)又称为有信息搜索(Informed Search),它是利用问题拥有的启发信息来引导搜索,达到减少搜索范围、降低问题复杂度的目的,这种利用启发信息的搜索过程称为启发式搜索。
A-Star(A*)算法的核心:将游戏背景分成一个又一个的格子,每个格子计算出一个估值,然后遍历起点的格子去找格子周围估值最小的节点作为下一步要走的路径,然后递归遍历,直到找到目标点
实现算法的关键点
1 将游戏背景划分成大小一样的正方形格子 ,我们把这些格子作为算法的基本单元,大小自定义
2 创建open队列(也就是一个数组),这个队列里面放可能会走的单元格
3 创建close队列(也是一个数组),这个队列里面放不能走的单元格,这里会包括已经走过的单元格和所有的障碍物
4 对所有的单元格进行估值
5 找到当前单元格周围的单元格,并且从这些单元格种找到估值最小的单元格
6 给每个走过的单元格加指针,记录所走过的路径,以便于打印最终路线
估价函数
在A*算法种用到的就是启发式搜索,而启发式搜索是利用拥有问题的启发信息来引导搜索的,所以我们需要把当前单元格周围的点都找出来进行估值,这个估值表示当前点到目标点的实际代价,如果到目标点的实际代价越高,那么说明要走的路就越长,因此,我们需要找到估值最低的作为下一步要走的路径
估价函数公式:fn(n) = g(n)+h(n)
其中:fn(n) 表示节点n的估值,g(n) 表示初始点到当前节点的实际代价,h(n)表示当前节点到目标点的实际代价,这里的实际代价就是这他们之间的最短距离
具体代码实现:
1 完成ui布局,这一步我们动态创建出一个 20 * 20 的正方形地图,每个格子大小也为20
![]()
![]()
2 估价函数封装
![]()
![]()
3 定义开始队列和结束队列数组 并且封装函数实现节点添加
![]()
/*
* 封装函数 实现开始队列中元素的添加
*/
function openFn(){
//1 需要把openArr中的第一个元素删除 并且返回给 nodeLi变量
var nodeLi = openArr.shift();
//2 把openArr中删除的这个li节点 添加到closeArr中 这里调用closeFn函数实现
closeFn(nodeLi);
}
/*
* 封装函数 实现结束队列中元素的添加
*
*/
function closeFn(nodeLi){
//open队列中删除的元素 被 push到close队列中
closeArr.push(nodeLi);
}
![]()
疑问?1openFn 什么时候执行? openArr 中什么时候有数据? 所以需要添加以下代码:
1) 在初始化函数中添加按钮的点击事件
![]()
//初始化函数
function init(){
createMap()
//点击按钮的时候 需要去收集可能走的路线
oBtn.onclick = function(){
openFn();
}
}
![]()
2) 在创建地图的时候,就要区分出 起始点和障碍物 并且把起点放在open队列数组中,把障碍物和放在close队列数组中
![]()
function createMap(){
//定义li的大小
var liSize = 20;
for(var i=0;i

经过上面两步,完整代码如下:

![]()
4 上面的步骤已经把 开始节点放到了open队列中 把障碍物放到了 close队列中,接下来我们要做的就是 寻找下一个要走的节点,并且把这个节点添加到close队列中
1) 封装函数查找周围的节点
![]()
/**
* 封装函数查找某个节点周围的节点
*/
function findLi(nodeLi){
//创建一个结果数组 把查找到的结果放到这个数组中
var result = [];
//循环所有的li节点 进行查找
for(var i=0;i

2) 上面函数封装好以后 需要在openFn函数中进行调用

function openFn(){
//nodeLi 表示 当前open队列中的元素 也就是说 先去除第一个起始节点
//shift 方法的作用: 把数组中的第一个元素删除,并且返回这个被删除的元素
var nodeLi = openArr.shift();
//如果nodeLi 和 endLi 一样了 那么证明已经走到目标点了 ,这个时候需要停止调用
if(nodeLi == endLi[0]){
return;
}
//把open队列中删除的元素 添加到 close队列中
closeFn(nodeLi)
//接下来 需要找到 nodeLi 周围的节点
findLi(nodeLi);
}

3) 经过上面的函数调用 在openArr数组中就已经 添加了 当前路径 周围的8个点,我们要从这8个点中去寻找一个估值最小的作为下一步要走的点
4) 接下来需要对openArr中的点进行估值排序

function openFn(){
//nodeLi 表示 当前open队列中的元素 也就是说 先去除第一个起始节点
//shift 方法的作用: 把数组中的第一个元素删除,并且返回这个被删除的元素
var nodeLi = openArr.shift();
//如果nodeLi 和 endLi 一样了 那么证明已经走到目标点了 ,这个时候需要停止调用
if(nodeLi == endLi[0]){
showPath();
return;
}
//把open队列中删除的元素 添加到 close队列中
closeFn(nodeLi)
//接下来 需要找到 nodeLi 周围的节点,并且对这些点进行估值
findLi(nodeLi);
//经过上面的步骤 已经能够找到相邻的元素了 接下来需要对这些元素的估值进行排序
openArr.sort(function(li1,li2){
return li1.num - li2.num
})
}

5) 经过上面的步骤 就已经能够确定下一步要走的点了 接下来要做的就是同样的操作 因此需要 递归调用openFn函数,在找到目标点的时候停止

function openFn(){
//nodeLi 表示 当前open队列中的元素 也就是说 先去除第一个起始节点
//shift 方法的作用: 把数组中的第一个元素删除,并且返回这个被删除的元素
var nodeLi = openArr.shift();
//如果nodeLi 和 endLi 一样了 那么证明已经走到目标点了 ,这个时候需要停止调用
if(nodeLi == endLi[0]){
showPath();
return;
}
//把open队列中删除的元素 添加到 close队列中
closeFn(nodeLi)
//接下来 需要找到 nodeLi 周围的节点
findLi(nodeLi);
//经过上面的步骤 已经能够找到相邻的元素了 接下来需要对这些元素的估值进行排序
openArr.sort(function(li1,li2){
return li1.num - li2.num
})
//进行递归操作 找下一步需要走的节点 在这个过程中,也需要执行相同的步
// 那就是查找相邻的节点 但是查找出来的结果可能和上一次的重复,也就是说上一次动作已经把这个元素添加到open队列中了
//那么就没有必要再进行push操作了 所以还需要在过滤函数中加一段代码
openFn();
}

5 打印出所走的路径
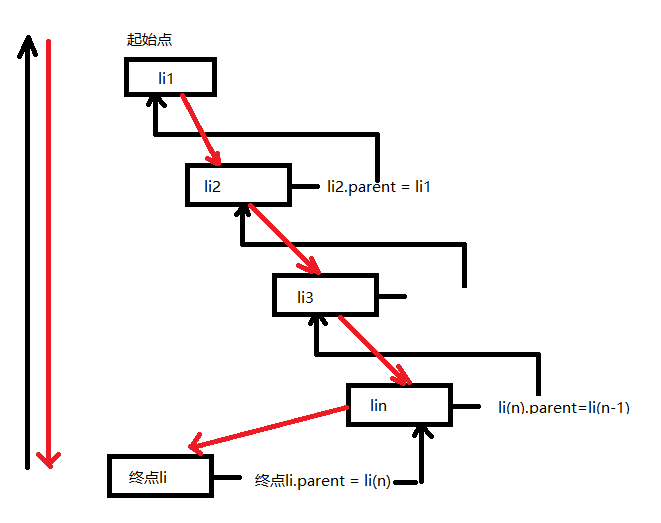
1) 给所走过的路径设置一个父指针,例如: 当前的节点应该有一个属性来存上一个节点,这样我们就可以从最后一个节点倒推出上面所有节点
在找到下一个要走的点的时候,把上一个已经走过的点挂载到下一个要走的点身上

/**
* 封装函数查找某个节点周围的节点
*/
function findLi(nodeLi){
//创建一个结果数组 把查找到的结果放到这个数组中
var result = [];
//循环所有的li节点 进行查找
for(var i=0;i

2) 封装一个函数来找到所有已经走过的点

//最终线路数组
var resultParent = [];
/**
* 定义一个函数来找到上一次走过的节点
*/
function findParent(li){
resultParent.unshift(li);
if(li.parent == beginLi[0]){
return;
}
findParent(li.parent);
}

3) 封装函数来打印 路径

/**
* 打印出所走过的路径
*/
function showPath(){
//closeArr中最后一个 就是 找到目标点的前一个位置 因为走过的位置都会被存放在closeArr中
var lastLi = closeArr.pop();
var iNow = 0;
//调用findParent函数 来找上一个节点
findParent(lastLi)
var timer = setInterval(function(){
resultParent[iNow].style.background = "red";
iNow++;
if(iNow == resultParent.length){
clearInterval(timer);
}
},500)
}

4) 在找到最终目标点的时候 调用打印路径函数

function openFn(){
//nodeLi 表示 当前open队列中的元素 也就是说 先去除第一个起始节点
//shift 方法的作用: 把数组中的第一个元素删除,并且返回这个被删除的元素
var nodeLi = openArr.shift();
//如果nodeLi 和 endLi 一样了 那么证明已经走到目标点了 ,这个时候需要停止调用
if(nodeLi == endLi[0]){
showPath();
return;
}
//把open队列中删除的元素 添加到 close队列中
closeFn(nodeLi)
//接下来 需要找到 nodeLi 周围的节点
findLi(nodeLi);
//经过上面的步骤 已经能够找到相邻的元素了 接下来需要对这些元素的估值进行排序
openArr.sort(function(li1,li2){
return li1.num - li2.num
})
//进行递归操作 找下一步需要走的节点 在这个过程中,也需要执行相同的步骤 那就是查找相邻的节点
//但是查找出来的结果可能和上一次的重复,也就是说上一次动作已经把这个元素添加到open队列中了
//那么就没有必要再进行push操作了 所以还需要在过滤函数中加一段代码
openFn();
}

走到这里 我们的算法已经基本实现
完整代码地址:https://github.com/dadifeihong/algorithm