备战秋招——算法与数据结构(4)
● 请你来手写一下快排的代码
参考回答:
int once_quick_sort(vector<int> &data, int left, int right)
{
int key = data[left];
while (left < right)
{
while (left < right && key <= data[right])
{
right--;
}
if (left < right)
{
data[left++] = data[right];
}
while (left < right && key > data[left])
{
left++;
}
if (left < right)
{
data[right--] = data[left];
}
}
data[left] = key;
return left;
}
int quick_sort(vector<int> & data, int left, int right)
{
if (left >= right )
{
return 1;
}
int middle = 0;
middle = once_quick_sort(data, left, right);
quick_sort(data, left, middle-1);
quick_sort(data, middle + 1, right);
};
● 请你手写一下快排的代码
参考回答:
nt once_quick_sort(vector<int> &data, int left, int right)
{
int key = data[left];
while (left < right)
{
while (left < right && key <= data[right])
{
right--;
}
if (left < right)
{
data[left++] = data[right];
}
while (left < right && key > data[left])
{
left++;
}
if (left < right)
{
data[right--] = data[left];
}
}
data[left] = key;
return left;
}
int quick_sort(vector<int> & data, int left, int right)
{
if (left >= right )
{
return 1;
}
int middle = 0;
middle = once_quick_sort(data, left, right);
quick_sort(data, left, middle-1);
quick_sort(data, middle + 1, right);
}
● 请问求第k大的数的方法以及各自的复杂度是怎样的,另外追问一下,当有相同元素时,还可以使用什么不同的方法求第k大的元素
参考回答:
首先使用快速排序算法将数组按照从大到小排序,然后取第k个,其时间复杂度最快为O(nlogn)
使用堆排序,建立最大堆,然后调整堆,知道获得第k个元素,其时间复杂度为O(n+klogn)
首先利用哈希表统计数组中个元素出现的次数,然后利用计数排序的思想,线性从大到小扫描过程中,前面有k-1个数则为第k大的数
利用快排思想,从数组中随机选择一个数i,然后将数组分成两部分Dl,Dr,Dl的元素都小于i,Dr的元素都大于i。然后统计Dr元素个数,如果Dr元素个数等于k-1,那么第k大的数即为k,如果Dr元素个数小于k,那么继续求Dl中第k-Dr大的元素;如果Dr元素个数大于k,那么继续求Dr中第k大的元素。
当有相同元素的时候,
首先利用哈希表统计数组中个元素出现的次数,然后利用计数排序的思想,线性从大到小扫描过程中,前面有k-1个数则为第k大的数,平均情况下时间复杂度为O(n)
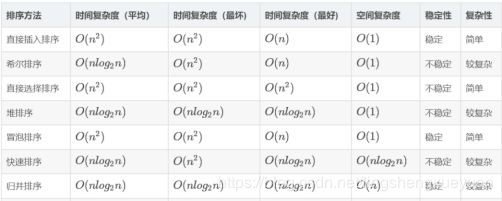
● 请你来介绍一下各种排序算法及时间复杂度
参考回答:
插入排序:对于一个带排序数组来说,其初始有序数组元素个数为1,然后从第二个元素,插入到有序数组中。对于每一次插入操作,从后往前遍历当前有序数组,如果当前元素大于要插入的元素,则后移一位;如果当前元素小于或等于要插入的元素,则将要插入的元素插入到当前元素的下一位中。
希尔排序:先将整个待排序记录分割成若干子序列,然后分别进行直接插入排序,待整个序列中的记录基本有序时,在对全体记录进行一次直接插入排序。其子序列的构成不是简单的逐段分割,而是将每隔某个增量的记录组成一个子序列。希尔排序时间复杂度与增量序列的选取有关,其最后一个值必须为1.
归并排序:该算法采用分治法;对于包含m个元素的待排序序列,将其看成m个长度为1的子序列。然后两两合归并,得到n/2个长度为2或者1的有序子序列;然后再两两归并,直到得到1个长度为m的有序序列。
冒泡排序:对于包含n个元素的带排序数组,重复遍历数组,首先比较第一个和第二个元素,若为逆序,则交换元素位置;然后比较第二个和第三个元素,重复上述过程。每次遍历会把当前前n-i个元素中的最大的元素移到n-i位置。遍历n次,完成排序。
快速排序:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
选择排序:每次循环,选择当前无序数组中最小的那个元素,然后将其与无序数组的第一个元素交换位置,从而使有序数组元素加1,无序数组元素减1.初始时无序数组为空。
堆排序:堆排序是一种选择排序,利用堆这种数据结构来完成选择。其算法思想是将带排序数据构造一个最大堆(升序)/最小堆(降序),然后将堆顶元素与待排序数组的最后一个元素交换位置,此时末尾元素就是最大/最小的值。然后将剩余n-1个元素重新构造成最大堆/最小堆。
● 请你说一说你知道的排序算法及其复杂度
参考回答:
1、冒泡排序:
从数组中第一个数开始,依次遍历数组中的每一个数,通过相邻比较交换,每一轮循环下来找出剩余未排序数的中的最大数并“冒泡”至数列的顶端。
稳定性:稳定
平均时间复杂度:O(n ^ 2)
2、插入排序:
从待排序的n个记录中的第二个记录开始,依次与前面的记录比较并寻找插入的位置,每次外循环结束后,将当前的数插入到合适的位置。
稳定性:稳定
平均时间复杂度:O(n ^ 2)
3、希尔排序(缩小增量排序):
希尔排序法是对相邻指定距离(称为增量)的元素进行比较,并不断把增量缩小至1,完成排序。
希尔排序开始时增量较大,分组较多,每组的记录数目较少,故在各组内采用直接插入排序较快,后来增量di逐渐缩小,分组数减少,各组的记录数增多,但由于已经按di−1分组排序,文件叫接近于有序状态,所以新的一趟排序过程较快。因此希尔 排序在效率上比直接插入排序有较大的改进。
在直接插入排序的基础上,将直接插入排序中的1全部改变成增量d即可,因为希尔排序最后一轮的增量d就为1。
稳定性:不稳定
平均时间复杂度:希尔排序算法的时间复杂度分析比较复杂,实际所需的时间取决于各次排序时增量的个数和增量的取值。时间复杂度在O(n ^ 1.3)到O(n ^ 2)之间。
4、选择排序:
从所有记录中选出最小的一个数据元素与第一个位置的记录交换;然后在剩下的记录当中再找最小的与第二个位置的记录交换,循环到只剩下最后一个数据元素为止。
稳定性:不稳定
平均时间复杂度:O(n ^ 2)
5、快速排序
1)从待排序的n个记录中任意选取一个记录(通常选取第一个记录)为分区标准;
2)把所有小于该排序列的记录移动到左边,把所有大于该排序码的记录移动到右边,中间放所选记录,称之为第一趟排序;
3)然后对前后两个子序列分别重复上述过程,直到所有记录都排好序。
稳定性:不稳定
平均时间复杂度:O(nlogn)
6、堆排序:
堆:
1、完全二叉树或者是近似完全二叉树。
2、大顶堆:父节点不小于子节点键值,小顶堆:父节点不大于子节点键值。左右孩子没有大小的顺序。
堆排序在选择排序的基础上提出的,步骤:
1、建立堆
2、删除堆顶元素,同时交换堆顶元素和最后一个元素,再重新调整堆结构,直至全部删除堆中元素。
稳定性:不稳定
平均时间复杂度:O(nlogn)
7、归并排序:
采用分治思想,现将序列分为一个个子序列,对子序列进行排序合并,直至整个序列有序。
稳定性:稳定
平均时间复杂度:O(nlogn)
8、计数排序:
思想:如果比元素x小的元素个数有n个,则元素x排序后位置为n+1。
步骤:
1)找出待排序的数组中最大的元素;
2)统计数组中每个值为i的元素出现的次数,存入数组C的第i项;
3)对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加);
4)反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1。
稳定性:稳定
时间复杂度:O(n+k),k是待排序数的范围。
9、桶排序:
步骤:
1)设置一个定量的数组当作空桶子; 常见的排序算法及其复杂度:
2)寻访序列,并且把记录一个一个放到对应的桶子去;
3)对每个不是空的桶子进行排序。
4)从不是空的桶子里把项目再放回原来的序列中。
时间复杂度:O(n+C) ,C为桶内排序时间。
● 请问海量数据如何去取最大的k个
参考回答:
1.直接全部排序(只适用于内存够的情况)
当数据量较小的情况下,内存中可以容纳所有数据。则最简单也是最容易想到的方法是将数据全部排序,然后取排序后的数据中的前K个。
这种方法对数据量比较敏感,当数据量较大的情况下,内存不能完全容纳全部数据,这种方法便不适应了。即使内存能够满足要求,该方法将全部数据都排序了,而题目只要求找出top K个数据,所以该方法并不十分高效,不建议使用。
2.快速排序的变形 (只使用于内存够的情况)
这是一个基于快速排序的变形,因为第一种方法中说到将所有元素都排序并不十分高效,只需要找出前K个最大的就行。
这种方法类似于快速排序,首先选择一个划分元,将比这个划分元大的元素放到它的前面,比划分元小的元素放到它的后面,此时完成了一趟排序。如果此时这个划分元的序号index刚好等于K,那么这个划分元以及它左边的数,刚好就是前K个最大的元素;如果index > K,那么前K大的数据在index的左边,那么就继续递归的从index-1个数中进行一趟排序;如果index < K,那么再从划分元的右边继续进行排序,直到找到序号index刚好等于K为止。再将前K个数进行排序后,返回Top K个元素。这种方法就避免了对除了Top K个元素以外的数据进行排序所带来的不必要的开销。
3.最小堆法
这是一种局部淘汰法。先读取前K个数,建立一个最小堆。然后将剩余的所有数字依次与最小堆的堆顶进行比较,如果小于或等于堆顶数据,则继续比较下一个;否则,删除堆顶元素,并将新数据插入堆中,重新调整最小堆。当遍历完全部数据后,最小堆中的数据即为最大的K个数。
4.分治法
将全部数据分成N份,前提是每份的数据都可以读到内存中进行处理,找到每份数据中最大的K个数。此时剩下NK个数据,如果内存不能容纳NK个数据,则再继续分治处理,分成M份,找出每份数据中最大的K个数,如果M*K个数仍然不能读到内存中,则继续分治处理。直到剩余的数可以读入内存中,那么可以对这些数使用快速排序的变形或者归并排序进行处理。
5.Hash法
如果这些数据中有很多重复的数据,可以先通过hash法,把重复的数去掉。这样如果重复率很高的话,会减少很大的内存用量,从而缩小运算空间。处理后的数据如果能够读入内存,则可以直接排序;否则可以使用分治法或者最小堆法来处理数据。
● 请问快排的时间复杂度最差是多少?什么时候时间最差
参考回答:
O(N2),元素本来倒序排列用时最多
● 请问稳定排序哪几种?
参考回答:
基数排序、冒泡排序、直接插入排序、折半插入排序、归并排序
● 请你介绍一下快排算法;以及什么是稳定性排序,快排是稳定性的吗;快排算法最差情况推导公式
参考回答:
1、快排算法
根据哨兵元素,用两个指针指向待排序数组的首尾,首指针从前往后移动找到比哨兵元素大的,尾指针从后往前移动找到比哨兵元素小的,交换两个元素,直到两个指针相遇,这是一趟排序,经常这趟排序后,比哨兵元素大的在右边,小的在左边。经过多趟排序后,整个数组有序。
稳定性:不稳定
平均时间复杂度:O(nlogn)
2、稳定排序
假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
快排算法是不稳定的排序算法。例如:
待排序数组:int a[] ={1, 2, 2, 3, 4, 5, 6};
若选择a[2](即数组中的第二个2)为枢轴,而把大于等于比较子的数均放置在大数数组中,则a[1](即数组中的第一个2)会到pivot的右边, 那么数组中的两个2非原序。
若选择a[1]为比较子,而把小于等于比较子的数均放置在小数数组中,则数组中的两个2顺序也非原序。
3、快排最差情况推倒
在快速排序的早期版本中呢,最左面或者是最右面的那个元素被选为枢轴,那最坏的情况就会在下面的情况下发生啦:
1)数组已经是正序排过序的。 (每次最右边的那个元素被选为枢轴)
2)数组已经是倒序排过序的。 (每次最左边的那个元素被选为枢轴)
3)所有的元素都相同(1、2的特殊情况)
因为这些案例在用例中十分常见,所以这个问题可以通过要么选择一个随机的枢轴,或者选择一个分区中间的下标作为枢轴,或者(特别是对于相比更长的分区)选择分区的第一个、中间、最后一个元素的中值作为枢轴。有了这些修改,那快排的最差的情况就不那么容易出现了,但是如果输入的数组最大(或者最小元素)被选为枢轴,那最坏的情况就又来了。