基于C++的简易RLC电路仿真器与滤波器仿真测试
电路建模分析与仿真算法
对于任意一个电路系统,我们基本上都能使用RLC和受控源进行等效,因此RLC系统的求解是任意一个系统求解的核心。
我们熟知,对于任意一个复杂的电路系统,基尔霍夫定律(Kirchhoff’s laws)总是成立的。选择使用基尔霍夫电压定律还是电流定理将带来两种电路分析方法:节点电压法与网孔电流法。
然而在通常的仿真算法中不会选择网孔电流法,因为该方法仅能处理平面电路,换言之对于一个不算复杂的立体电路结构(例如正四面体类型的纯电阻电路)网孔电流法就失效了。例如,以SPICE为代表的系列仿真器采用改进的节点电压法对电路进行建模计算。
谈到SPICE,其发展是一个漫长的历史,几十年间SPICE这个名字都在业界如雷贯耳。1971年之前,绝大多数电路仿真器的开发都在军方的掌控下,直到1971年,以Laurence Nagel为代表的七人小组在加州大学伯克利分校开发了SPICE,其最大的特点是改进了矩阵求解方式,在计算机运算速度极低的时代,节省了大量时间与研究经费。
稀疏矩阵的求解带来的成效是立竿见影的。
我们知道电路若干个节点之间并非都存在连接,换言之一个电路矩阵矩阵往往是稀疏的,以下举一个简单的例子。
[ + 1 R 1 − 1 R 1 0 0 0 0 0 0 0 0 − 1 R 1 + 1 R 1 + 1 R 2 + s C 1 − 1 R 2 0 0 0 − s C 1 0 0 0 0 − 1 R 2 + 1 R 2 + 1 R 3 + 1 R 6 − 1 R 3 0 0 0 − 1 R 6 0 0 0 0 − 1 R 3 + 1 R 3 + 1 R 4 + s C 2 − 1 R 4 0 0 0 − s C 2 0 0 0 0 − 1 R 4 + 1 R 4 + 1 R 5 + s C 3 − 1 R 5 0 0 0 − s C 3 0 0 0 0 − 1 R 5 + 1 R 5 0 0 0 0 0 − s C 1 0 0 0 0 + s C 1 + 1 R 9 + 1 R 7 − 1 R 9 0 0 0 0 − 1 R 6 0 0 0 − 1 R 9 + 1 R 6 + 1 R 9 + 1 R 10 + s C 4 − 1 R 10 0 0 0 0 − s C 2 0 0 0 − 1 R 10 + s C 2 + 1 R 10 + 1 R 11 + 1 R 8 − 1 R 11 0 0 0 0 − s C 3 0 0 0 − 1 R 11 + s C 3 + 1 R 11 + s C 5 ] [ v 0 ( s ) v 1 ( s ) v 2 ( s ) v 3 ( s ) v 4 ( s ) v 5 ( s ) v 6 ( s ) v 7 ( s ) v 8 ( s ) v 9 ( s ) ] [ i 0 ( s ) 0 0 0 0 0 0 0 0 0 ] \begin{bmatrix} +\frac{1}{R_{1}}&-\frac{1}{R_{1}}&0&0&0&0&0&0&0&0\\ -\frac{1}{R_{1}}&+\frac{1}{R_{1}}+\frac{1}{R_{2}}+sC_{1}&-\frac{1}{R_{2}}&0&0&0&-sC_{1}&0&0&0\\ 0&-\frac{1}{R_{2}}&+\frac{1}{R_{2}}+\frac{1}{R_{3}}+\frac{1}{R_{6}}&-\frac{1}{R_{3}}&0&0&0&-\frac{1}{R_{6}}&0&0\\ 0&0&-\frac{1}{R_{3}}&+\frac{1}{R_{3}}+\frac{1}{R_{4}}+sC_{2}&-\frac{1}{R_{4}}&0&0&0&-sC_{2}&0\\ 0&0&0&-\frac{1}{R_{4}}&+\frac{1}{R_{4}}+\frac{1}{R_{5}}+sC_{3}&-\frac{1}{R_{5}}&0&0&0&-sC_{3}\\ 0&0&0&0&-\frac{1}{R_{5}}&+\frac{1}{R_{5}}&0&0&0&0\\ 0&-sC_{1}&0&0&0&0&+sC_{1}+\frac{1}{R_{9}}+\frac{1}{R_{7}}&-\frac{1}{R_{9}}&0&0\\ 0&0&-\frac{1}{R_{6}}&0&0&0&-\frac{1}{R_{9}}&+\frac{1}{R_{6}}+\frac{1}{R_{9}}+\frac{1}{R_{10}}+sC_{4}&-\frac{1}{R_{10}}&0\\ 0&0&0&-sC_{2}&0&0&0&-\frac{1}{R_{10}}&+sC_{2}+\frac{1}{R_{10}}+\frac{1}{R_{11}}+\frac{1}{R_{8}}&-\frac{1}{R_{11}}\\ 0&0&0&0&-sC_{3}&0&0&0&-\frac{1}{R_{11}}&+sC_{3}+\frac{1}{R_{11}}+sC_{5} \end{bmatrix} \begin{bmatrix} v_{0}(s)\\v_{1}(s)\\v_{2}(s)\\v_{3}(s)\\v_{4}(s)\\v_{5}(s)\\v_{6}(s)\\v_{7}(s)\\v_{8}(s)\\v_{9}(s) \end{bmatrix} \begin{bmatrix} i_{0}(s)\\0\\0\\0\\0\\0\\0\\0\\0\\0\end{bmatrix} ⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡+R11−R1100000000−R11+R11+R21+sC1−R21000−sC10000−R21+R21+R31+R61−R31000−R610000−R31+R31+R41+sC2−R41000−sC20000−R41+R41+R51+sC3−R51000−sC30000−R51+R5100000−sC10000+sC1+R91+R71−R910000−R61000−R91+R61+R91+R101+sC4−R1010000−sC2000−R101+sC2+R101+R111+R81−R1110000−sC3000−R111+sC3+R111+sC5⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡v0(s)v1(s)v2(s)v3(s)v4(s)v5(s)v6(s)v7(s)v8(s)v9(s)⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡i0(s)000000000⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
大家不要被这个例子吓到了!CSDN对博客中公示的处理一直不太好
这是一个简单的只有10个节点的电路,里面包含16个器件。我们注意到系数矩阵存在大量的0项,并且我们必须要关注到:矩阵的主对角线是始终非零的,这是一个非常好的性质:我们无需使用交换矩阵P,只需不断选择对角线上的元素为主元就可以完成LU分解。目前不同的求解器对于LU分解的处理各不相同,直接LU分解依然需要使用高斯消元,针对稀疏矩阵、病态矩阵的求解有消去树、波前法等,这些都是LU分解的实现形式。LU分解的可并行性使得其可以在GPU或者是FPGA之类的平台上运行。
对于任意一个电路,确定拓扑,添加激励后就可以求解每一个节点的电压。事实上节点电压与节点以及节点之间的导纳有关,这个结论在以前的博文里有提到,当时我们将电路局限在直流电路中,现在我们需要将其拓宽至复数域。
对于复数域电路响应求解我们有一些有力的手段,拉普拉斯变换就是其中之一。
拉氏变换能让我们透过s区域观察电路的本质属性。
| 器件 | s域 |
|---|---|
| R | R R R |
| L | s L sL sL |
| C | 1 s C \frac{1}{sC} sC1 |
当激励源为 I ( s ) I(s) I(s)时,该RLC系统的传递函数可以写成
H ( s ) = V o ( s ) V i ( s ) H(s)=\frac{V_o(s)}{V_i(s)} H(s)=Vi(s)Vo(s)
当需要求解系统幅频特性时,只需要
∣ A ( j w ) ∣ = ∣ H ( s ) ∣ s = j w ∣ = ∣ V o ( j w ) V i ( j w ) ∣ |A(jw)|=|H(s)|_{s=jw}|=|\frac{V_o(jw)}{V_i(jw)}| ∣A(jw)∣=∣H(s)∣s=jw∣=∣Vi(jw)Vo(jw)∣
求解相频特性时,只需要
ϕ ( j w ) = a r c t a n i m [ H ( j w ) ] r e [ H ( j w ) ] \phi(jw)=arctan\frac{im[H(jw)]}{re[H(jw)]} ϕ(jw)=arctanre[H(jw)]im[H(jw)]
矩阵求解
两年前的博客中介绍了使用了一种基于高斯消元(Gaussian Elimination)的LUP分解求解矩阵的一种算法,利用这种算法可以在 O ( n 3 ) O(n^3) O(n3)的时间复杂度内完成矩阵的求解,特别是当矩阵规模较大或是稀疏矩阵的情况下LUP分解是占有一定优势的。当然在通常的计算中不是非常喜欢使用LUP分解这种技术,因为他实在有些复杂,更适合普通应用的也许是高斯消元法。
高斯消元法的思路是,对于一个线性方程组
[ a 11 a 12 . . . a 1 n a 21 a 22 . . . a 2 n . . . . . . . . . . . . a n 1 a n 2 a n 3 . . a n n ] [ x 1 x 2 . . . x n ] = [ b 1 b 2 . . . b n ] \begin{bmatrix} a_{11} & a_{12}&. &. &. &a_{1n}\\ a_{21} &a_{22} &. &. &. & a_{2n}\\ .& .& .& & & .\\ .& .& & .& & .\\ .& .& & & .&. \\ a_{n1}&a_{n2} &a_{n3} &. &. &a_{nn} \end{bmatrix} \begin{bmatrix} x_{1}\\ x_{2}\\ .\\.\\ .\\ x_{n}\end{bmatrix}= \begin{bmatrix}b_{1}\\ b_{2}\\ .\\ .\\ .\\ b_{n}\end{bmatrix} ⎣⎢⎢⎢⎢⎢⎢⎡a11a21...an1a12a22...an2...an3........a1na2n...ann⎦⎥⎥⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎢⎡x1x2...xn⎦⎥⎥⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎢⎢⎡b1b2...bn⎦⎥⎥⎥⎥⎥⎥⎤
可以对每行选择一个主元,进行若干次线性运算(倍乘、相加),得到一个三角阵,接着对这个三角阵 进行迭代求解。
对于下三角阵,有递推公式
x m = b m − ∑ i = 1 m − 1 a m i x i a m m x_{m}=\frac{b_{m}-\sum_{i=1}^{m-1}a_{mi}x_{i}}{a_{mm}} xm=ammbm−∑i=1m−1amixi
可以求得其解,注意这不是一个闭公式。
由于程序设计最大的节点数量为1000个节点,实在没有使用LU分解的必要。
void Gauss_solve(complex* ans, int n) //高斯消元,用于主对角线非零的矩阵求解
{
int i, j, k;
for (i = 0; i < n; ++i)
A[i][n] = B[i]; //初始化常数矩阵
for (i = 0; i < n - 1; ++i)//转换为上三角阵
{
for (j = i + 1; j < n; ++j)
{
complex temp = A[j][i] / A[i][i];
for (k = 0; k <= n; ++k)
A[j][k] = A[j][k] - A[i][k] * temp;
}
}
ans[0] = A[0][n] / A[0][0];
complex sum(0, 0);
ans[n - 1] = A[n - 1][n] / A[n - 1][n - 1];
for (i = n - 2; i >= 0; i--) //求解上三角矩阵
{
for (j = n - 1; j > i; j--)
sum = sum + A[i][j] * ans[j];
ans[i] = (A[i][n] - sum) / A[i][i];
sum.real = 0;
sum.img = 0;
}
}
拓扑读取
电路拓扑采用网表的形式输入,例如那个有点恐怖的矩阵对应的电路拓扑对应的网表如下
N0 N1 R1 1000
N1 N2 R2 100
N2 N3 R3 1000
N3 N4 R4 1000
N4 N5 R5 1000
N1 N6 C1 0.1
N2 N7 R6 100
N3 N8 C2 0.1
N4 N9 C3 0.01
N6 N7 R9 1000
N7 N8 R10 100
N8 N9 R11 100
N6 N10 R7 1000
N7 N10 C4 2.1
N8 N10 R8 1000
N9 N10 C5 0.1
IN N0
OUT N5
GND N10
网表中对每个节点进行编号,在最后给出了激励源的输入位置、探头位置与参考地的位置,这样无论电路有多么复杂、是否是一个平面电路,上述形式的网表都可以将其准确表述。
测试
在写下这篇博客的时候,博主已经编写了一些基本功能,例如传递函数输出、幅频特性曲线绘制等,以下是测试详情。
3阶低通滤波器

滤波器的拓扑如上图所示,这是一个3阶的RC低通滤波,其网表可以表示为
N0 N1 R1 1000
N1 N2 R2 1000
N2 N3 R3 1000
N1 N4 C1 0.1
N2 N4 C2 0.1
N3 N4 C3 0.1
IN N0
OUT N3
GND N4
生成的节点电压矩阵如下
[ + 1 R 1 − 1 R 1 0 0 − 1 R 1 + 1 R 1 + 1 R 2 + s C 1 − 1 R 2 0 0 − 1 R 2 + 1 R 2 + 1 R 3 + s C 2 − 1 R 3 0 0 − 1 R 3 + 1 R 3 + s C 3 ] [ v 0 ( s ) v 1 ( s ) v 2 ( s ) v 3 ( s ) ] = [ i 0 ( s ) 0 0 0 ] \begin{bmatrix} +\frac{1}{R_{1}}&-\frac{1}{R_{1}}&0&0\\ -\frac{1}{R_{1}}&+\frac{1}{R_{1}}+\frac{1}{R_{2}}+sC_{1}&-\frac{1}{R_{2}}&0\\ 0&-\frac{1}{R_{2}}&+\frac{1}{R_{2}}+\frac{1}{R_{3}}+sC_{2}&-\frac{1}{R_{3}}\\ 0&0&-\frac{1}{R_{3}}&+\frac{1}{R_{3}}+sC_{3} \end{bmatrix} \begin{bmatrix} v_{0}(s)\\v_{1}(s)\\v_{2}(s)\\v_{3}(s) \end{bmatrix}= \begin{bmatrix} i_{0}(s)\\0\\0\\0\end{bmatrix} ⎣⎢⎢⎡+R11−R1100−R11+R11+R21+sC1−R2100−R21+R21+R31+sC2−R3100−R31+R31+sC3⎦⎥⎥⎤⎣⎢⎢⎡v0(s)v1(s)v2(s)v3(s)⎦⎥⎥⎤=⎣⎢⎢⎡i0(s)000⎦⎥⎥⎤
由于博主在程序中调用了 LaTeX \LaTeX{} LATEX进行排版,因此可以直接输出电路拓扑信息,同时使用了pgfplots宏包进行绘图。
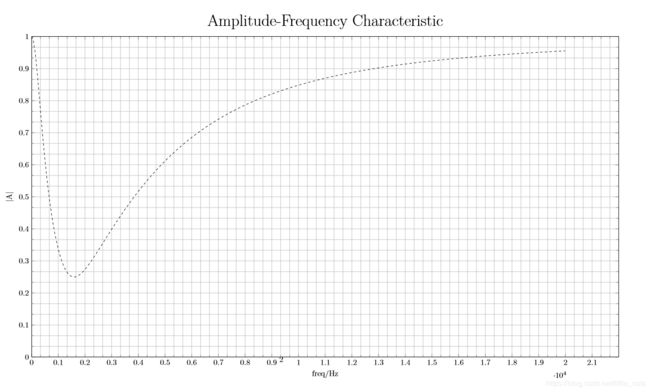
该电路的幅频特性曲线如图所示

这与PSPICE仿真结果一致。
带阻滤波器
N0 N1 R1 1000
N1 N2 R2 1000
N1 N4 C1 0.1
N0 N3 C2 0.1
N3 N2 C3 0.1
N3 N4 R3 1000
IN N0
OUT N2
GND N4
生成的节点电压矩阵如下
[ + 1 R 1 + s C 2 − 1 R 1 0 − s C 2 − 1 R 1 + 1 R 1 + 1 R 2 + s C 1 − 1 R 2 0 0 − 1 R 2 + 1 R 2 + s C 3 − s C 3 − s C 2 0 − s C 3 + s C 2 + s C 3 + 1 R 3 ] [ v 0 ( s ) v 1 ( s ) v 2 ( s ) v 3 ( s ) ] = [ i 0 ( s ) 0 0 0 ] \begin{bmatrix} +\frac{1}{R_{1}}+sC_{2}&-\frac{1}{R_{1}}&0&-sC_{2}\\ -\frac{1}{R_{1}}&+\frac{1}{R_{1}}+\frac{1}{R_{2}}+sC_{1}&-\frac{1}{R_{2}}&0\\ 0&-\frac{1}{R_{2}}&+\frac{1}{R_{2}}+sC_{3}&-sC_{3}\\ -sC_{2}&0&-sC_{3}&+sC_{2}+sC_{3}+\frac{1}{R_{3}} \end{bmatrix} \begin{bmatrix} v_{0}(s)\\v_{1}(s)\\v_{2}(s)\\v_{3}(s) \end{bmatrix}= \begin{bmatrix} i_{0}(s)\\0\\0\\0\end{bmatrix} ⎣⎢⎢⎡+R11+sC2−R110−sC2−R11+R11+R21+sC1−R2100−R21+R21+sC3−sC3−sC20−sC3+sC2+sC3+R31⎦⎥⎥⎤⎣⎢⎢⎡v0(s)v1(s)v2(s)v3(s)⎦⎥⎥⎤=⎣⎢⎢⎡i0(s)000⎦⎥⎥⎤