机器学习第九周 主成分分析PCA
机器学习 第九周 主成分分析
学习目标
知识点描述:无监督降维:主成分分析法
学习目标:
- 主成分分析法的思想及其原理
- PCA算法的实现及调用
- 数据降维应用:降噪&人脸识别
学习内容
数据降维1:主成分分析法思想及原理
数据降维2:PCA算法的实现及使用
数据降维3:降维映射及PCA的实现与使用
数据降维之应用:降噪&人脸识别
学习ing
主成分分析 PCA principal Component Analysis, 是一种使用最广泛的数据降维算法(非监督的机器学习方法),其主要用途在于降维,也可以用来消减回归分析和聚类分类中变量的数目。
主成分分析法的步骤:
第一步:样本归0;第二步:找到样本映射后方差最大的单位向量
v a r ( x ) = 1 m ∑ i = 1 m ( x i − x ‾ ) 2 , x ‾ = 0 样 本 归 0 , 即 所 有 数 值 减 去 均 值 var(x)=\frac{1}{m}\sum_{i=1}^{m}(x_i-\overline{x})^2,\overline{x}=0 样本归0 ,即所有数值减去均值 var(x)=m1i=1∑m(xi−x)2,x=0样本归0,即所有数值减去均值
映 射 后 v a r ( x ) = 1 m ∑ i = 1 m ∣ ∣ X 映 射 i ∣ ∣ 2 映射后var(x)=\frac{1}{m}\sum_{i=1}^{m}||X_{映射}^i||^2 映射后var(x)=m1i=1∑m∣∣X映射i∣∣2
X ( i ) w = ∣ ∣ X ( I ) ∣ ∣ . ∣ ∣ w ∣ ∣ c o s θ , 当 w 时 单 位 向 量 时 X^{(i)}w = ||X^{(I)}||.||w||cos \theta,当w时单位向量时 X(i)w=∣∣X(I)∣∣.∣∣w∣∣cosθ,当w时单位向量时
= ∣ ∣ X ( i ) ∣ ∣ c o s θ = ∣ ∣ X p r o j e c t ( i ) ∣ ∣ =||X^{(i)}||cos \theta = ||X_{project}^{(i)}|| =∣∣X(i)∣∣cosθ=∣∣Xproject(i)∣∣
主成分分析的目标是:
求 w , 使 得 v a r ( X p r o j e c t ) = 1 m ( X ( i ) w ) 2 最 大 求w,使得var(X_{project})=\frac{1}{m}(X^{(i)}w)^2最大 求w,使得var(Xproject)=m1(X(i)w)2最大
像之前目标函数有了,求最大值的参数。可以使用搜索策略,梯度上升法。
( a k + 1 , b k + 1 ) = ( a k + 1 + η ∂ L ∂ a , b k + 1 + η ∂ L ∂ b ) (a_{k+1},b_{k+1})=(a_{k+1}+\eta \frac{\partial L}{\partial{a}},b_{k+1}+\eta \frac{\partial L}{\partial{b}}) (ak+1,bk+1)=(ak+1+η∂a∂L,bk+1+η∂b∂L)

求解第一个主成分
import numpy as np
import matplotlib.pyplot as plt
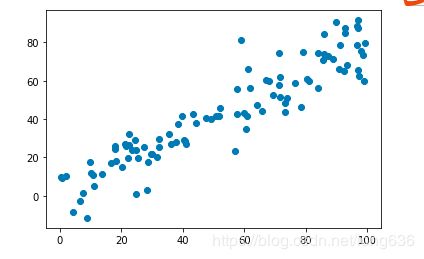
X = np.empty([100,2])
X[:,0] = np.random.uniform(0.,100.,size =100)
X[:,1] = 0.75 * X[:,0] + 3. + np.random.normal(0.,10.,size = 100)
plt.scatter(X[:,0],X[:,1])
plt.show()
#第一步归0 ,axis按列计算均值
def demean(X):
return (X - np.mean(X, axis= 0 ))
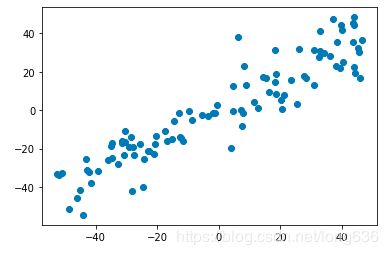
X_demean = demean(X)
plt.scatter(X_demean[:, 0],X_demean[:, 1])
plt.show()
#X_demean
#目标函数的定义
def f(w,X):
return np.sum(X.dot(w)**2) /len(X[:,0])
#梯度
def df_math(w,X):
return 2*X.T.dot(X.dot(w)) / len(X[:,0])
#验证梯度调式
def df_debug(w, X, epsilon = 0.0001):
res = np.empty(len(w))
for i in range(len(w)):
w_1 = w.copy()
w_1[i] += epsilon
w_2 = w.copy
w_2[i] -= epsilon
res[i] = (f(w_1,X) - f(w_2, X)) / (2*epsilon)
return res
def direction(w):#求第二范数,计算单位向量
return w / np.linalg.norm(w)
#梯度上升法代码
def gradient_ascent(X,initial_w ,eta ,n_iters=1e4, epsilon = 1e-8):
w = direction(initial_w)
cur_iter = 0
while cur_iter < n_iters:
last_w = w
gradient = df_math( w, X)
w = last_w + eta * gradient
#w每次计算前均是单位向量
w = direction(w)
if abs(f(w,X) - f(last_w,X)) < epsilon :
break
cur_iter += 1
return w
#
initial_w = np.random.random(X.shape[1])
eta = 0.001
w = gradient_ascent(X, initial_w , eta)
w
array([0.77535907, 0.63152063])
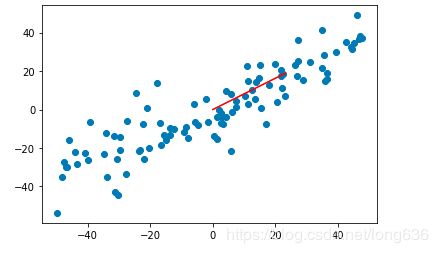
plt.scatter(X_demean[:,0] ,X_demean[:,1])
plt.plot([0,w[0]*30],[0,w[1]*30] ,color='red')# x,y (0,0) (21,18) 连线
y = w[0] * X_demean[:,0] + w[1] * X_demean[:,1]
plt.plot(X)
plt.show()
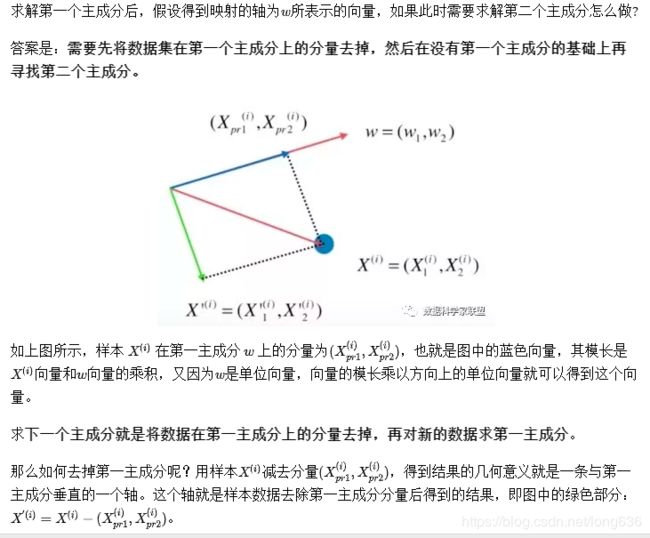
求解第二个主成分
X_new = X - X.dot(w).reshape(-1,1)*w #w?
plt.scatter(X_new[:,0],X_new[:,1])
plt.show()
w_new = gradient_ascent(X_new ,initial_w , eta)
w_new
#array([-0.63150239, 0.77537393])
求解前n个主成分
#求解前n个主成分
def first_n_componet(n, X,eta = 0.001, n_iters = 1e4, epsilon = 1e-8):
X_pca = X.copy()
X_pca = demean(X_pca)
res = []
for i in range(n):
initial_w = np.random.random(X_pca.shape[1])
w = gradient_ascent(X_pca, initial_w, eta)
res.append(w)
X_pca = X_pca - X_pca.dot(w).reshape(-1,1) * w
return res
res = first_n_componet(2, X)
res
#[array([0.7676373 , 0.64088453]), array([-0.64086321, 0.7676551 ])]
K维的选择影响最终的结果精度,在sklearn中定义解释方差比例,通过提前定义解释的百分比pca.explained_variance_ratio,可以得到降维的k。继而根据前n个主成分进行求解。
from sklearn.decomposition import PCA
pca = PCA(n_components = 1)#直接传入主成分个数
pca.fit(X)
X_reduction = pca.transform(X) #降维
pca = PCA(0.95)
pca.fit(X_train)
# 输出:
PCA(copy=True, iterated_power='auto', n_components=0.95, random_state=None,
svd_solver='auto', tol=0.0, whiten=False)
对于一组数据,通过传入解释方差比例,能够得到其准确率条件下的降维数据。然后再根据降维后的结果去做其他运算。