有序数组中的二分查找
A朋友去面试,上来第一道手撕算法题就是有序旋转数组中的查找。
仔细回忆了一下,这常规题啊,之前还仔细分析过各种情况。
……
啊,我忘记上次是怎么分析各种情况的了。想吃植入记忆芯片的药。
为了增强理解和记忆,仔细分析一下二分查找。
二分查找模版
二分查找又叫折半查找,要求数组/序列满足一定的有序性,根据某些判断条件不断缩小查找的范围。因为每次范围缩小为原来的一半,所以叫二分或者折半。
如此说来,问题就在于:
- 折半选择的判断条件;即在什么条件下选择左一半,什么条件下选择右一半
- 停止条件;即在什么条件下停止查找
以下是九章算法建议的二分法的模版,当left + 1 < right时,不断二分查找。之所以此处需要left + 1 < while 而不是left <= right,是因为此处二分采用的是left = mid 或者right = mid,当left + 1 = right时,例如数组元素 3,4。目标值是4,left指针会一直等于mid指针,一直停在第一个元素位置,代码陷入死循环。所以要求当元素个数小于等于2的时候需要跳出while循环单独处理。
(当然,可以使用mid = right - 1或者 mid = left + 1 来规避mid指针停在某一位置不动而陷入死循环的问题。没有强制要求,个人使用习惯吧。如果有好坏之分,欢迎评论指导)
// 待查找数组int[] nums
// 目标值 target
if(nums == null || nums.length == 0)
return -1;
int left = 0, right = nums.length - 1;
while(left + 1 < right){
int mid = left + (right - left) / 2;
if(target == nums[mid]) //停止条件
return mid; //停止查找
if(target < nums[mid]) // 折半条件
right = mid; //选择左半部分继续查找
else
left = mid; //选择右半部分继续查找
}
if(nums[left] == target)
return left;
if(nums[right] == target)
return right;
return -1;
一、查找第一个与target相同的元素
LintCode: https://www.lintcode.com/problem/first-position-of-target/description
题目描述:升序数组nums中查找目标值target,如果存在返回目标值第一次出现的位置索引,如果不存在返回-1。(默认数组中不会含有 -1)。
简析:区别就在于目标元素可能连续出现多次,需要返回第一次出现的位置。折半的条件没有发生变化,而停止的条件发生了变化。遇到目标元素不一定就停止查找,还要求该元素是第一次出现才停止。
直接思路:二分法找到目标元素之后,向前遍历,直到找到第一次出现的位置,返回该位置。
public class Solution {
/**
* @param nums: The integer array.
* @param target: Target to find.
* @return: The first position of target. Position starts from 0.
*/
public int binarySearch(int[] nums, int target) {
// write your code here
if(nums == null || nums.length == 0)
return -1;
int left = 0, right = nums.length - 1;
while(left + 1 < right){
int mid = left + (right - left) / 2;
if(target == nums[mid]){
//继续向前遍历,查找第一次出现位置
while(mid - 1 >= left && nums[mid - 1]== target){
mid --;
}
return mid;
}
if(target < nums[mid])
right = mid;
else
left = mid;
}
if(nums[left] == target)
return left;
if(nums[right] == target)
return right;
return -1;
}
}
优化思路二:遇到nums[mid] == target时,以该位置为right,继续向前寻找。直到left + 1 == right。
public class Solution {
/**
* @param nums: The integer array.
* @param target: Target to find.
* @return: The first position of target. Position starts from 0.
*/
public int binarySearch(int[] nums, int target) {
if (nums == null || nums.length == 0) {
return -1;
}
int left = 0, right = nums.length - 1;
while (left + 1 < right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target)
right = mid; //当找到目标元素之后,继续在(left, 目标元素] 区间查找
else if (nums[mid] < target)
left = mid;
else
right = mid;
}
//跳出循环时,可能是 [目标元素(第一次),目标元素(第二次)], 即存在重复
//也可能是 [其他元素,目标元素],即无重复
//此处顺序必须是先判断left再判断right!!!想想为什么
if (nums[left] == target) {
return left;
}
if (nums[right] == target) {
return right;
}
return -1;
}
}
为什么优化思路在跳出while循环之后,判断target元素是必须先判断left,再判断right。
因为当跳出循环时,left和right对应的元素是[目标元素(第一次),目标元素(第二次)]或者[第一个小于target的元素,目标元素(第一次)]。如果先判断left,返回的就不是第一次出现的位置啦。返回的是第二次出现的位置啦。
二、查找最后一个与target相等的元素
在lintcode上没有找到只查找最后一次出现位置的题,下面的题是同时查找第一次出现的位置和最后一次出现的位置。借该题分析以下查找最后一个与target相等的元素
LintCode:https://www.lintcode.com/problem/find-first-and-last-position-of-element-in-sorted-array/description
题目描述:非递减序列nums,寻找target元素第一次出现的位置和最后一次出现的位置。
public class Solution {
/**
* @param nums: the array of integers
* @param target:
* @return: the starting and ending position
*/
public List searchRange(List nums, int target) {
if(nums == null && nums.size() == 0)
return null;
List list = new ArrayList<>();
int left = 0, right = nums.size() - 1;
// 查找target第一次出现的位置
while(left + 1 < right){
int mid = left + (right - left) / 2;
if(nums.get(mid) == target)
right = mid; //从该位置往前找
else if(nums.get(mid) > target)
right = mid;
else
left = mid;
}
if(nums.get(left) == target) //优先判断left位置的元素是否等于target
list.add(left);
else if(nums.get(right) == target)
list.add(right);
else
list.add(-1);
//查找target最后一次出现的位置
left = 0; right = nums.size() - 1;
while(left + 1 < right){
int mid = left + (right - left) / 2;
if(nums.get(mid) == target)
left = mid; //从该位置往后找
else if(nums.get(mid) > target)
right = mid;
else
left = mid;
}
if(nums.get(right) == target) //优先判断right位置的元素是否等于target
list.add(right);
else if(nums.get(left) == target)
list.add(left);
else
list.add(-1);
return list;
}
}
可以看粗,查找第一次出现和最后一次出现的思路和代码就是姊妹篇。区别就在于:
- 当nums[mid] == target时的处理方式:寻找第一次出现位置则往前找,寻找最后一次出现则往后找。
- 当跳出循环时,left和right对应的元素是
[目标元素(倒数第二次),目标元素(最后一次)]或者[目标元素(最后一次)],第一个大于target的元素]。如果先判断left,返回的就不是第一次出现的位置啦。返回的是第二次出现的位置啦。当跳出while循环之后查找target的顺序:寻找第一次出现位置则先查right,寻找最后一次出现则先查right。
三、查找第一个大于或等于target的元素
Lintcode:https://www.lintcode.com/problem/search-insert-position/description
题目描述:题目是给定一个排序数组(无重复元素)和一个目标值,如果在数组中找到目标值则返回索引。如果没有,返回到它将会被按顺序插入的位置。
简析: 题目要么返回target所在的位置,要么返回第一个比target大的元素位置。二分查找模版当中,最后将范围缩小到由left和right指向的两个元素。如果target在数组中存在,那么target就是nums[left]或者nums[right]。如果target在数组中不存在,nums[left]或者nums[right]则是离target最近和次近的元素。
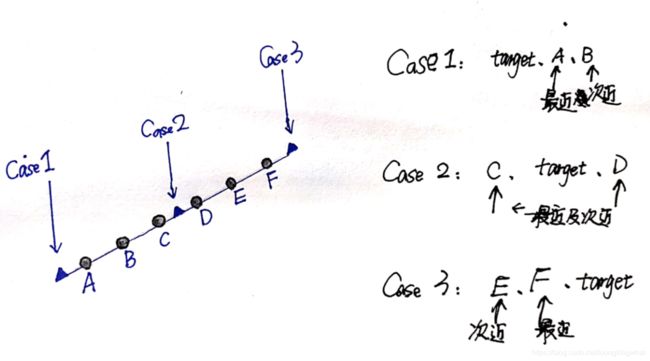
那么,其实思路就是判断跳出while循环之后的数组。如果存在则返回位置。如果不存在根据不同的case判断插入位置。
public class Solution {
/**
* @param A: an integer sorted array
* @param target: an integer to be inserted
* @return: An integer
*/
public int searchInsert(int[] A, int target) {
// write your code here
if(A == null || A.length == 0)
return 0;
int left = 0, right = A.length - 1;
while(left + 1 < right){
int mid = left + (right -left) / 2;
if(A[mid] == target)
return mid;
if(A[mid] > target)
right = mid;
else
left = mid;
}
//跳出while循环之后根据target值与A[left]、A[right]的关系确定返回值
if(target <= A[left])
return left;
else if(target <= A[right])
return right;
else
return right + 1;
}
}
如果已经熟练掌握了模版解决上述三个问题的方法,下面看看升级版本的二分查找。
检验自己是否掌握:请直接点击对应链接进行Coding,说一千道一万,不如动手写一遍。写完可能才会重新认识自己哈哈哈
上面三个大类的题目都是基于严格单调的升序序列或者存在相等值的非递减序列。下面开始讨论不是升级的情况:旋转数组。旋转数组就是将非递减序列C分成A和B两个部分,将原本处于前半部分的A移到B的后面。例如 1 2 3 4 5 6变成 5 6 1 2 3 4,或者 3 4 5 6 1 2。
四、非递减数组中目标元素target出现的次数
答题链接:https://www.acwing.com/problem/content/63/
题目描述:统计一个数字在排序数组中出现的次数。
例如输入排序数组[1, 2, 3, 3, 3, 3, 4, 5]和数字3,由于3在这个数组中出现了4次,因此输出4。
简析:通过二分寻找第一次出现的位置firsPosition和最后一次出现的位置lastPosition,最终的次数就是cnt = firstPosition == -1 ? 0 : lastPosition - firstPosition + 1。
按照上面的思路,寻找第一次出现的位置,while(left + 1 < right)中当A[mid] == target时right = mid即可,不产生return。当while循环结束之后,在A[left]和A[right]当中确认第一次出现的位置;
寻找最后一次出现的位置,与上面思路一致,while(left + 1 < right)中当A[mid] == target时right = mid即可。也是最终在A[left]和A[right]当中确认最后一次出现的位置。
class Solution {
public int getNumberOfK(int[] nums, int k) {
if(nums == null || nums.length ==0)
return 0;
int left = 0, right = nums.length - 1;
int firstPosition = 0, lastPosition = 0;
//S1:找到第一个target出现的位置
while(left + 1 < right){
int mid = left + (right - left) / 2;
if(nums[mid] >= k)
right = mid;
else
left = mid;
}
if(nums[left] == k){
firstPosition = left;
}else if(nums[right] == k)
firstPosition = right;
else
return 0; //如果不存在target直接返回0
//S2:找到最后一个target出现的位置
left = 0; right = nums.length - 1;
while(left + 1 < right){
int mid = left + (right - left) / 2;
if(nums[mid] <= k)
left = mid;
else
right = mid;
}
if(nums[right] == k)
lastPosition = right;
else
lastPosition = left;
//返回长度结果
return lastPosition - firstPosition + 1;
}
}
五、搜索旋转排序数组I
LintCode:https://www.lintcode.com/problem/find-minimum-in-rotated-sorted-array/description
题目描述:假设有一个排序的按未知的旋转轴旋转的数组(比如,0 1 2 4 5 6 7 可能成为4 5 6 7 0 1 2)。给定一个目标值进行搜索,如果在数组中找到目标值返回数组中的索引位置,否则返回-1。假设数组中不存在重复的元素。
简析:要想达到log(n)的复杂度,仍然需要使用二分法。旋转数组与普通数组的二分情况更加复杂,如下图所示。折半查找的条件发生了变化。存在一些特殊情况不再满足“mid值比target大,就找前半段,mid值小于target,就找后半段”。那么解决该题其实就是针对特殊情况单独判断即可。
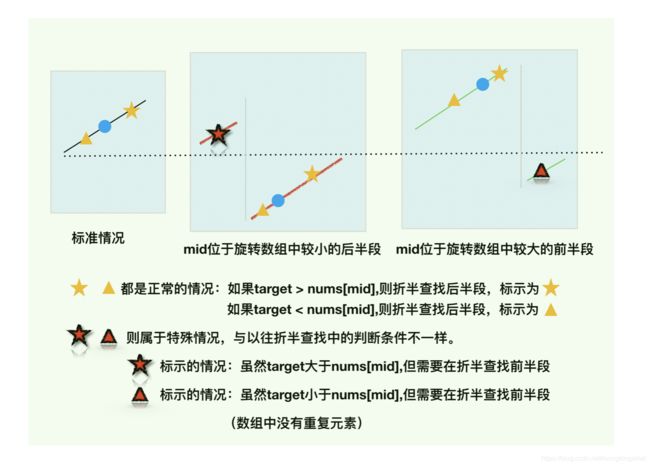
因为此题目中没有相等的数据,所以确定特殊情况比较简单,通过mid所处的位置+target所处的位置就可以将特殊情况与其他一般情况区分开。
public class Solution {
/**
* @param A: an integer rotated sorted array
* @param target: an integer to be searched
* @return: an integer
*/
public int search(int[] A, int target) {
// write your code here
if(A == null || A.length ==0)
return -1;
int left = 0, right = A.length - 1;
while(left + 1 < right){
int mid = left + (right - left) / 2;
if(A[mid] == target)
return mid;
if(A[mid] > target){
if(target < A[left] && A[mid] > A[left]) //通过定位target和mid的位置确定特殊情况
left = mid; //处理mid值大于target时存在的特殊情况(对应上图的特殊三角形)
else //处理特殊情况外的其他情况
right = mid; //其他的情况都满足二分的基本原则:mid值大于target,折半查找前半段
}else{
if(target > A[left] && A[mid] < A[left])
right = mid; //处理mid值小于target时存在的特殊情况(对应上图的特殊五角星)
else
left = mid;//其他的情况都满足二分的基本原则:mid值小于target,折半查找后半段
}
}
//此时跳出while循环时,可能的情况是:
//A[left] < A[right] ,例如 4,10
//或者A[left] > A[right], 例如 10,6,后面讲为什么还会出现该种情况。
if(A[left] == target)
return left;
if(A[right] == target)
return right;
return -1;
}
}
六、搜索旋转排序数组II
Lintcode:https://www.lintcode.com/problem/search-in-rotated-sorted-array-ii/description
题目描述:针对可能存在重复元素的旋转排序数组,例如[3,4,4,5,7,0,1,2]查找target。只需要返回true或者false,不用出现位置。
简析:没有重复元素的旋转数组搜索,比普通的二分查找增加了折半的判断条件,处理特殊情况。当出现重复元素的时候,对一般二分的判断条件没有影响。
下图展示了重复元素具体的影响及解决办法(我觉得讲的挺糙的,有更好的方法欢迎留言)
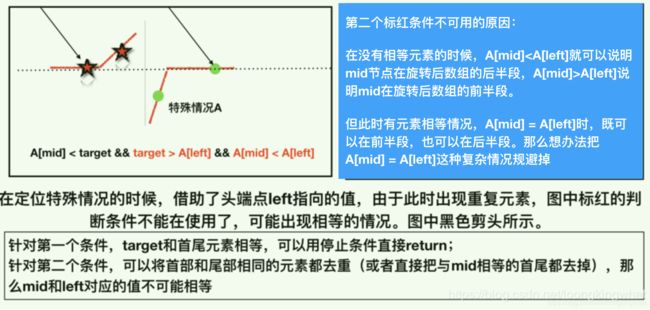
/**
* @author wanglong
* @brief
* @date 2019-08-23 01:07
*/
public class Solution {
/**
* @param A: an integer ratated sorted array and duplicates are allowed
* @param target: An integer
* @return: a boolean
*/
public boolean search(int[] A, int target) {
// write your code here
if(A == null || A.length == 0)
return false;
int left = 0, right = A.length - 1 ;
while(left + 1 < right){
//去除头部的重复元素,只保留一次即可
while(left + 1 <= right && A[left] == A[left+1])
left ++;
//去除尾部的重复元素,只保留一次即可
while(left <= right - 1 && A[right] == A[right - 1])
right --;
int mid = left + (right - left) / 2;
if(A[mid] == target || A[left] == target || A[right] == target)
return true;
if(A[mid] > target){
if(target < A[left] && A[mid] > A[left]) //special min
left = mid;
else
right = mid;
}
if(A[mid] < target){
if(target > A[left] && A[mid] < A[left]) //specail max
right = mid;
else
left = mid;
}
}
if(A[left] == target)
return true;
if(A[right] == target)
return true;
return false;
}
}
关于该题还有一种理解方法,主要while循环部分不同。
while (start + 1 < end) {
int mid = (start + end) / 2;
if (A[mid] == target) {
return true;
}
if (A[mid] == A[end]) {
end--;
}
else if (A[mid] == A[start]) {
start++;
}
if (A[mid] < A[end]) {
if (A[mid] < target && target <= A[end]) {
start = mid;
}
else {
end = mid;
}
}
else if (A[mid] > A[start]) {
if (A[start] <= target && target < A[mid]) {
end = mid;
}
else {
start = mid;
}
}
}
七、寻找旋转数组的最小值
Lintcode:https://www.lintcode.com/problem/find-minimum-in-rotated-sorted-array/description
题目描述:旋转数组中寻找最小值
简析:此处没有target了,所以停止条件发生了变化。以前当遇到target值直接return,此处直接return的情况是nums[left]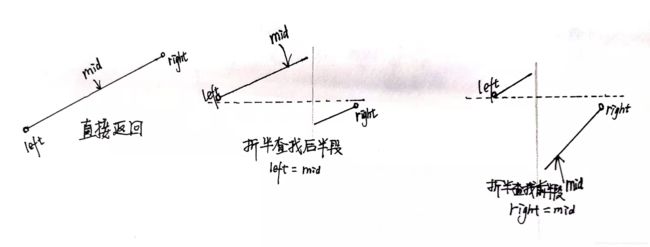
代码:
public class Solution {
/**
* @param nums: a rotated sorted array
* @return: the minimum number in the array
*/
public int findMin(int[] nums) {
// write your code here
if(nums == null || nums.length == 0)
return 0;
int left = 0, right = nums.length - 1;
while(left + 1 < right){
int mid = left + (right - left) / 2;
//直接返回
if(nums[left] < nums[right])
return nums[left];
else if(nums[mid] > nums[left])
left = mid; //折半查找后半段
else
right = mid; //折半查找前半段
}
return nums[left] > nums[right] ? nums[right] : nums[left];
}
}
参考文章:你真的会写二分查找吗https://www.cnblogs.com/luoxn28/p/5767571.html