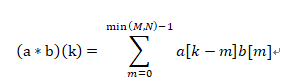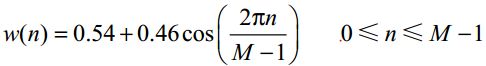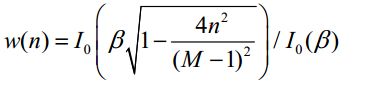Numpy基础教程—其它相关函数

本教程适合于numpy基础入门，更多详尽内容请阅读官网http://www.numpy.org/，此篇为numpy基础学习教程系列之其它相关函数篇，倾向于实践用法，后续还会推出一系列numpy其它方面的教程，欢迎广大圈友一起交流学习，并指出其中的错误。

 

注意：以下np为import numpy as np中的np标识符

 

 

傅里叶变换

 

    np.fft.fft(array)：对信号array进行傅里叶变换

    np.fft.ifft(transformed)：还原信号

    注意：numpy.linalg模块中的fftshift函数可以将FFT输出中的直流分量移动到频谱的中央，ifftshift函数是其逆操作

 

 

 

 

排序函数

 

    numpy.lexsort函数支持对数组按指定行或列的顺序排序，是间接排序，lexsort不修改原数组，返回索引。

    注意：如果参数为元组，最后一个作为主要的排序的key，倒数第二个作为次要的排序的key

    注意：对于多维数组排序，默认按最后一行元素由小到大排序，返回最后一行元素排序后索引所在位置。返回的索引数组ind，则a[ind]就是排序后的数组。

 

import numpy as np

>>> a

array([[2,  7,  4,  2],

       [35,  9,  1,  5],

       [22,12,  3,  2]])

 

按最后一列顺序排序

>>>a[np.lexsort(a.T)]

 

array([[2,  7,  4,  2],

       [35,  9,  1,  5],

       [22,12,  3,  2]])

 

按最后一列逆序排序

>>>a[np.lexsort(-a.T)]

array([[35,  9,  1,  5],

       [2,  7,  4,  2],

       [22,12,  3,  2]])

 

按第一列顺序排序

>>> a[np.lexsort(a[:,::-1].T)]

array([[2,  7,  4,  2],

       [22,12,  3,  2],

       [35,  9,  1,  5]])

 

按最后一行顺序排序

>>>a.T[np.lexsort(a)].T

array([[2,  4,  7,  2],

       [5,  1,  9, 35],

       [2,  3, 12, 22]])

 

按第一行顺序排序

>>>a.T[np.lexsort(a[::-1,:])].T

array([[2,  2,  4,  7],

       [5, 35,  1,  9],

       [2, 22,  3, 12]]

 

np.sort(array)：对数组array进行排序，返回排序后的视图，并不改变原数组。

array.sort()：对数组array进行排序，原地排序。

np.msort(array)：对数组array进行排序，返回排序后的视图，并不改变原数组。

np.argsort(array)：间接排序，返回排序后的索引数组。

np.sort_complex(complex_numbers)：对复数进行排序，先按照实部后虚部的顺序进行排序。

 

 

 

 

网格函数

 

np.meshgrid用于从数组a和b产生网格。生成的网格矩阵A和B大小是相同的。它也可以是更高维的。

[A,B]=np.meshgrid(a,b)
生成size(b)* size(a)大小的矩阵A和B。它相当于a从一行重复增加到size(b)行，把b转置成一列再重复增加到size(a)列。因此命令等效于：

A=np.mat(np.ones(np.size(b))).T*a;
B=np.mat(b).T*np.ones(np.size(a))

 

如下所示：

>> a=np.arange(1,3,1)

a =

     1     2

>> b=np.arange(3,6,1)

b =

     3     4     5

>> [A,B]=meshgrid(a,b)

A =

     1     2
     1     2
     1     2

B =

     3     3
     4     4
     5     5

 

>> [B,A]=meshgrid(b,a)

B =

     3     4     5
     3     4     5

A =

     1     1     1
     2     2     2

 

 

计算卷积

 

numpy.convolve(a,v, mode=’full’)：numpy函数中的卷积函数库
参数： 
  a:(N,)输入的一维数组 
  b:(M,)输入的第二个一维数组 
  mode:{‘full’, ‘valid’, ‘same’}参数可选 
    ‘full’　默认值，返回每一个卷积值，长度是N+M-1,在卷积的边缘处，信号不重叠，存在边际效应。 
    ‘same’　返回的数组长度为max(M, N),边际效应依旧存在。 
    ‘valid’ 　返回的数组长度为max(M,N)-min(M,N)+1,此时返回的是完全重叠的点，边缘点无效。

公式：

 

 

其中，k-m 0，m 0，k的最大值为N+M-2

 

实例：

    a = np.arange(4)

    b = np.array([2,3,1,5])

    print np.convolve(a,b)

结果：[0,2,7,13,16,13,15]

 

 

自定义ufunc函数

 

 

np.frompyfunc(func,nin,nout)：将一个计算单个元素的函数转换为ufunc函数。

  参数:func—函数

       nin—输入参数的个数

       nout—func返回值的个数

实例：

 

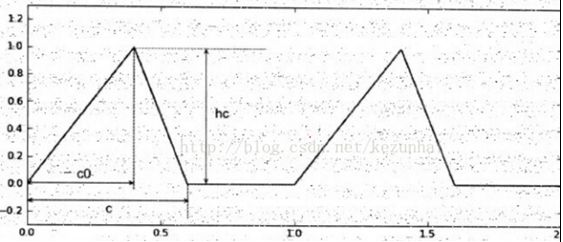
def triangle_wave(x,c,c0,hc):

    x= x-int(x)    #周期为1，取小数部分计算

    ifx>=c:

        R=0.0

    elif:x

        R = x/c0*hc

    else:

        r = (c-x)/(c-c0)*hc

    returnr

 

triangle_wave_ufunc =np.frompyfunc(triangle_wave,4,1)

x = np.linspace(0,2,100)

y2 = triangle_wave_ufunc(x,0.6,0.4,1.0)

注意：triangle_wave_ufunc所返回数组的元素类型是object，因此还需要调用数组的astype()方法将其转换为双精度浮点数组。

 

 

 

 

 

np.vectorize()函数

 

使用vectorize( )可以实现和frompyfunc()类似的功能，但它可以通过otypes参数指定返回数组的元素类型。otypes参数可以是一个表示元素类型的字符串，也可以是一个类型列表，使用列表可以描述多个返回数组的元素类型，如将上面的代码改成vectorize()，则为：

triangle_wave_vec = np.vectorize(triangle_wave,otypes=[np.float])

x = np.linspace(0,2,100)

y3 = triangle_wave_vec(x,0.6,0.4,1.0)
 

 

窗函数：窗函数是信号处理领域常用的数学函数，这些窗函数在给定的区间之外取值为0

 

巴特利特窗是一种三角形平滑窗

window = np.bartlett(42)

 布莱克曼窗形式上为三项余弦值的加和

 

black = np.blackman(num)：该函数唯一的参数就是输出点的数量，如果数量为0或小于0，则返回一个空数组。

 

 

 

汉明窗（Hammingwindow）形式上是一个加权的余弦函数，公式如下：

Numpy中的hamming函数返回汉明窗。该函数唯一的参数就是输出点的数量，如果参数为0或小于0，则返回一个空数组。

 

凯泽窗是以贝塞尔函数定义的，公式如下：

这里的I0即为零阶的贝塞尔函数。NumPy中的kaiser函数返回凯泽窗。该函数的第一个参数为输出点的数量。如果数量为0或小于0，则返回一个空数组。第二个参数为β值。

注意：np.i0(array)：i0位第一类修正的零阶贝塞尔函数。