R语言之数据预处理笔记

数据预处理是将 原始数据 转化成能够用于建模的一致数据的过程，它是分析流程中非常关键的一个环节！！！！
首先，载入需要的R包
caret ：提供机器学习模型及拟合效果的系统交互界面
e1071:各类计量经济和机器学习的延伸，我们使用其中的naiveBayes函数进行朴素贝叶斯判别
gridExtra:绘图辅助功能，将不同图形组合在一起成为图表
lattice:建立在核心绘图能力上的格子框架图形
imputeMissings:填补缺失值
RANN:应用K-邻近算法
corrplot:相关矩阵的高级可视化
nnet:拟合单个潜层级的神经网络模型
car:回归模型解释和可视化工具
gpairs:广义散点图
reshape2:灵活重构和整合数据，主要有两个函数melt()和dcast()
psych:心理计量学方法和抽样调查分析，尤其是因子分析和项目反映模型plyr:可以将数据分割成更小的数据，然后对分割后的数据进行一些操作，最后把操作的结果汇总
tidyr:清理糅合数据的包，主要函数是spread()和gather()

> library(caret)
> library(e1071)
> library(gridExtra)
> library(lattice)
> library(imputeMissings)
> library(RANN)
> library(corrplot)
> library(nnet)
> library(car)
> library(gpairs)
> library(reshape2)
> library(psych)
> library(plyr)
> library(tidyr)

数据清理

检查数据

1.有哪些变量
2.变量怎样分布
3.是不是存在错误的观测

以下是读取服装消费者数据

> sim.dat=read.csv("https://raw.githubusercontent.com/happyrabbit/DataScientistR/master/Data/SegData.csv")

由上图，灰色框勾选的即为所有的变量。Q1…Q10貌似合理，min为1，max为5，gender,house,online_exp,store_trans,online_trans,segment看上去也合理。
而其他（红色区域勾选部分）存在异常，其中age和store_exp中存在离群值，income中存在缺失值。

异常值初步处理：

1.将这些值设置成缺失状态

> sim.dat$age[which(sim.dat$age>100)]=NA
> sim.dat$store_exp[which(sim.dat$store_exp<0)]=NA
> summary(subset(sim.dat,select=c("age","income")))
      age            income      
 Min.   :16.00   Min.   : 41776  
 1st Qu.:25.00   1st Qu.: 85832  
 Median :36.00   Median : 93869  
 Mean   :38.58   Mean   :113543  
 3rd Qu.:53.00   3rd Qu.:124572  
 Max.   :69.00   Max.   :319704  
 NA's   :1       NA's   :184     
> 

2.缺失值填补
-（1）中位数或众数填补
即用含有缺失值变量中的中位数或众数填补缺失值

#impute()为imputeMissings包中的函数
> demo_imp=impute(sim.dat,method="median/mode")
> summary(demo_imp[,1:5])
      age           gender        income       house       store_exp      
 Min.   :16.00   Female:554   Min.   : 41776   No :432   Min.   :  155.8  
 1st Qu.:25.00   Male  :446   1st Qu.: 87896   Yes:568   1st Qu.:  205.1  
 Median :36.00                Median : 93869             Median :  329.8  
 Mean   :38.58                Mean   :109923             Mean   : 1357.7  
 3rd Qu.:53.00                3rd Qu.:119456             3rd Qu.:  597.3  
 Max.   :69.00                Max.   :319704             Max.   :50000.0  
> 

这种方法简单，工作中常用，但是有一个缺点，单独对每个变量进行缺失值填补而忽略变量间的关系，故有的时候不太准确。
也可用preProcess()函数进行中位数填补，效果与impute(）函数相同。
（2）K-近邻填补(KNN)
“物以类聚”思想的统计学表达
K-近邻方法建立在距离之上，其基本思路是：
对于含有缺失值的样本，寻找该样本的邻居，然后用这些邻居的观测均值对样本缺失值进行填补。
寻找邻居根据的是样本点间的距离，故各个变量的标量要统一，不然尺度大的变量会在决定距离上占主导作用。
显示所有变量类型

#显示所有变量类型
> lapply(sim.dat,class)
$age
[1] "integer"

$gender
[1] "factor"

$income
[1] "numeric"

$house
[1] "factor"

$store_exp
[1] "numeric"

$online_exp
[1] "numeric"

$store_trans
[1] "integer"

$online_trans
[1] "integer"

$Q1
[1] "integer"

$Q2
[1] "integer"

$Q3
[1] "integer"

$Q4
[1] "integer"

$Q5
[1] "integer"

$Q6
[1] "integer"

$Q7
[1] "integer"

$Q8
[1] "integer"

$Q9
[1] "integer"

$Q10
[1] "integer"

$segment
[1] "factor"

#用preProcess()函数实现KNN填补
> imp=preProcess(sim.dat,method="knnImpute",k=5)
 #找到非数值型变量
> idx=which(lapply(sim.dat,class)=="factor")
#过滤掉非数值型变量

> demo_imp=predict(imp,sim.dat[,-idx])
> summary(demo_imp[,1:3])
      age                 income           store_exp       
 Min.   :-1.5910972   Min.   :-1.43989   Min.   :-0.43345  
 1st Qu.:-0.9568733   1st Qu.:-0.53732   1st Qu.:-0.41574  
 Median :-0.1817107   Median :-0.37606   Median :-0.37105  
 Mean   : 0.0000156   Mean   : 0.02389   Mean   :-0.00042  
 3rd Qu.: 1.0162678   3rd Qu.: 0.21540   3rd Qu.:-0.27437  
 Max.   : 2.1437770   Max.   : 4.13627   Max.   :17.52734  

注意：
1.用preProcess()函数进行KNN填补时，函数会自动对数据进行标准化
2.KNN算法无法对整行缺失的观测进行填补（缺失点找不到邻居）

查找完全缺失的样本（整行缺失）

#构造完全缺失样本
> temp=rbind(sim.dat,rep(NA,ncol(sim.dat)))
>  idx=apply(temp,1,function(x) sum(is.na(x)))
> as.vector(which(idx==ncol(temp)))
[1] 1001

（3）装袋树填补（提高精确度，但是计算量很大）
基本思路：用除缺失值后的剩下的变量训练装袋树，再用训练出来的树来对缺失值进行预测。

#preProcess为caret包中函数
> imp=preProcess(sim.dat,method="bagImpute")
> demo_imp=predict(imp,sim.dat)
> summary(demo_imp[,1:5])
      age           gender        income       house       store_exp      
 Min.   :16.00   Female:554   Min.   : 41776   No :432   Min.   :  155.8  
 1st Qu.:25.00   Male  :446   1st Qu.: 86616   Yes:568   1st Qu.:  205.1  
 Median :36.00                Median : 94739             Median :  329.0  
 Mean   :38.58                Mean   :114690             Mean   : 1357.7  
 3rd Qu.:53.00                3rd Qu.:123726             3rd Qu.:  597.3  
 Max.   :69.00                Max.   :319704             Max.   :50000.0  
> 

中心化和标量化

中心化：变量观测值-变量均值
中心化后变量观测均值为0
标量化：（变量观测值-变量均值）/变量标准差
标量化后变量标准差为1
标量化和中心化保证了变量的线性组合是基于组合后的新变量能够解析的原始变量中的方差
（基于方差的变量线性组合的模型有PCA(主成分分析),PLS(偏最小二乘分析),EFA(探索性因子分析）等。）

> incom=sim.dat$income
#均值，忽略NA
> mux=mean(incom,na.rm=T)
#标准差，忽略NA
> sdx=sd(incom,na.rm=T)
#中心化
> tr1=income-mux
#标准化
> tr2=tr1/sdx
> summary(data.frame(cbind(incom,tr1,tr2)))
     incom             tr1              tr2         
 Min.   : 41776   Min.   :-71767   Min.   :-1.4399  
 1st Qu.: 85832   1st Qu.:-27711   1st Qu.:-0.5560  
 Median : 93869   Median :-19674   Median :-0.3947  
 Mean   :113543   Mean   :     0   Mean   : 0.0000  
 3rd Qu.:124572   3rd Qu.: 11029   3rd Qu.: 0.2213  
 Max.   :319704   Max.   :206161   Max.   : 4.1363  
 NA's   :184      NA's   :184      NA's   :184      

如上所示，tr1均值为0，但是取值跨度依旧很大，tr2均值为0，标准差为1
对多个变量进行中心化和标量化

> sim.dat=sim.dat1
> sdat=subset(sim.dat,select=c("age","income"))
#center为中心化，scale为标量化
> trans=preProcess(sdat,method=c("center","scale"))
> transformed=predict(trans,sdat)
> summary(transformed)
      age              income       
 Min.   :-1.5911   Min.   :-1.4399  
 1st Qu.:-0.9569   1st Qu.:-0.5560  
 Median :-0.1817   Median :-0.3947  
 Mean   : 0.0000   Mean   : 0.0000  
 3rd Qu.: 1.0163   3rd Qu.: 0.2213  
 Max.   : 2.1438   Max.   : 4.1363  
 NA's   :1         NA's   :184      

有偏分布

若模型要求变量服从一定的对称分布，则需要进行数据变换去除分布的偏度

> set.seed(1000)
> par(mfrow=c(1,2),oma=c(2,2,2,2))
#抽取1000个自由度为2的卡方分布，右偏分布
> x1=rchisq(1000,2,ncp=0)
#得到左偏分布变量x2
> x2=max(x1)-x1
#skewness为e1071包中函数,用于偏度计算
> plot(density(x2),family="Songti SC",main=paste("left,level=",round(skewness(x2),2)),xlab="x2")
> plot(density(x1),family="Songti SC",main=paste("right,level=",round(skewness(x1),2)),xlab="x1")

如上图，左偏时偏度小于0，右偏时偏度大于0，绝对值越大，偏离程度越大

如上图，skew是偏度，trimmed是修剪后的平均值（去掉最大值最小值后），上图阔以看出store_exp中明显存在离群点

> trans=preProcess(dat_bc,method=c("BoxCox"))
> trans
 #1000个样本量，2个变量
Created from 1000 samples and 2 variables

Pre-processing:
  - Box-Cox transformation (2)
  - ignored (0)
#两个变量对应的参数估计值
Lambda estimates for Box-Cox transformation:
0.1, 0.7
> transformed=predict(trans,dat_bc)
> par(mfrow=c(1,2),oma=c(2,2,2,2))
> hist(dat_bc$store_trans,main="original data",xlab="store_trans",family="Songti SC")
> hist(transformed$store_trans,main="changed data",xlab="store_trans",family="Songti SC")

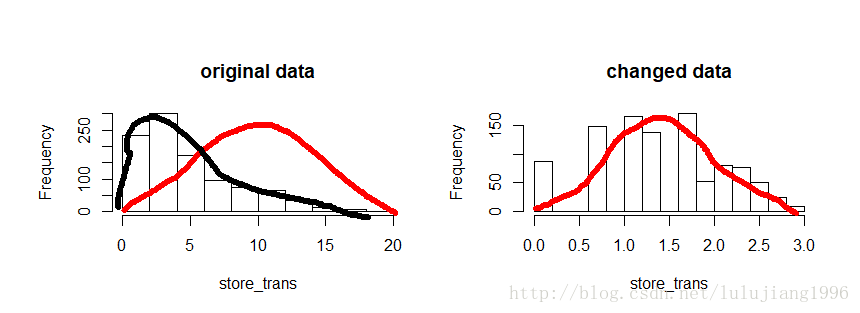
如上图，处理前，分布明显左偏，处理后情况显著改善。
BoxCoxTrans()也可进行Box-Cox变换，但是只能作用于单个数值变量，不能像之前那样对一个数据框中的列一次性进行变换。

处理离群点

判断离群点常用方法：箱线图和直方图的一些基本可视化

> sdat=subset(sim.dat,select=c("age","income","store_exp","online_exp","store_trans","online_trans"))
> par(oma=c(2,2,1,2)
+ )
#scatterplotMatrix为car包中的函数，用于绘制散点图矩阵

> scatterplotMatrix(sdat,diagona1="boxplot",smoother=FALSE)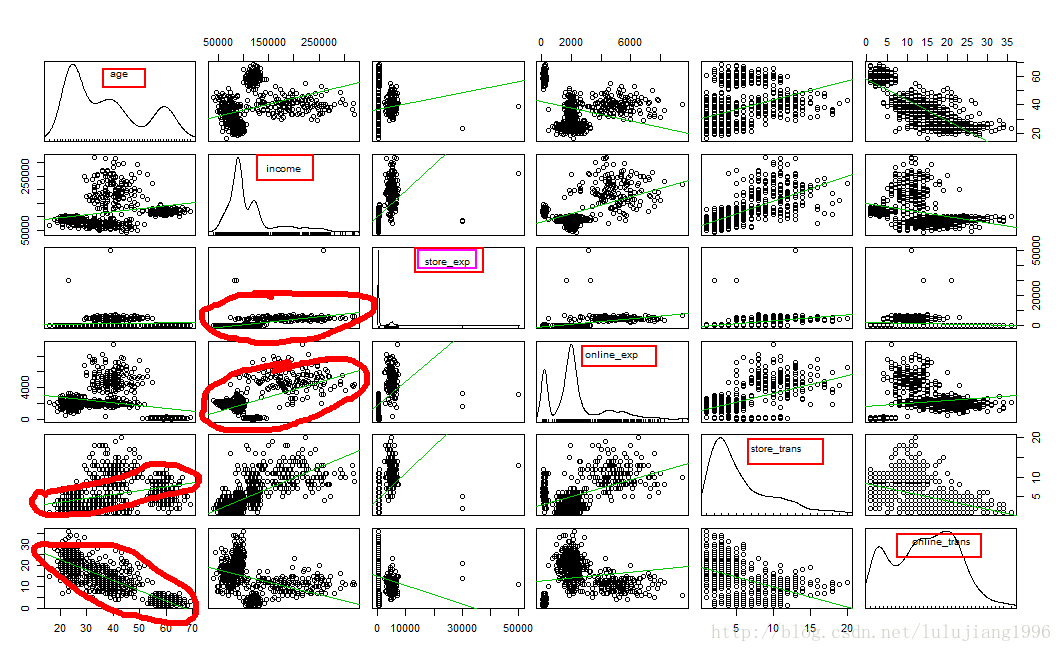

如上图，store_exp中明显有离群点，此外阔以看出，年龄和在线交易次数呈负相关，和实体交易次数成正相关，等等。
此外，可用z分值来判断可能的离群点

> ymad=mad(na.omit(sdat$income))
There were 50 or more warnings (use warnings() to see the first 50)
> zs=(sdat$income-mean(na.omit(sdat$income)))/ymad
> sum(na.omit(zs>3.5))
[1] 59
> 

如上，有59个离群点
离群点的影响主要取决于你使用的模型，有的模型对离群值很敏感（线性回归，逻辑回归等），有的模型对离群点具有抗性（树模型，支持向量机模型等），此外，离群点和错误的观测不一样，它是真实的观测，不能随意删除。
使用空间表示变换，将自变量的取值映射到高维的球面上。
注意：
1.变换前需要对自变量标准化
2.变换操作的对象是所有的自变量
3.必要时，必须在空间表示变换之前移除变量，不能在之后移除。

> sdat=sim.dat[,c("income","age")]
> imp=preProcess(sdat,method=c("knnImpute"),k=5)
> sdat=predict(imp,sdat)
> transformed=spatialSign(sdat)
> par(mfrow=c(1,2),oma=c(2,2,2,2))
> transformed=as.data.frame(transformed)
> plot(income~age,data=sdat,col="blue",main="before",family="Songti SC")
There were 15 warnings (use warnings() to see them)
> plot(income~age,data=transformed,col="blue",main="latter",family="Songti SC")
There were 43 warnings (use warnings() to see them)
> 

共线性

> sdat=subset(sim.dat,select=c("age","income","store_exp","online_exp","store_trans","online_trans"))
There were 50 or more warnings (use warnings() to see the first 50)
> imp=preProcess(sdat,method="bagImpute")
> sdat=predict(imp,sdat)
> correlation=cor(sdat)
> par(oma=c(2,2,2,3))
> corrplot.mixed(correlation,order="hclust",t1.pos="lt",upper="ellipse")

相关性越接近0颜色越浅且形状越接近圆，相关性不等于0的我们设置为椭圆。相关性越大，椭圆越窄，蓝色代表正相关，红色代表负相关，椭圆方向也随相关性正负变化。
两个变量高度相关意味着它们含有重复的信息，我们不需要将它们同时留在模型中，因为变量高度相关会导致参数估计量极为不稳定。

今天就先到这里了哈，我们明天继续~