多元函数的极值&牛顿迭代法

多元函数的极值

多元函数求极值的方法其他网页已经写了很多，在此不多叙述。在此不多赘述。简单给出结论：
（1）一元函数求极值：对于一阶连续函数： 必须满足 $f^{\prime }(x)=0且f^{\prime \prime }(x)̸=0$

（2）二元函数求极值：对于二阶连续函数： 必须满足 $f_x(x,y)=0$ && $f_y(x,y)=0$，且

其中，$(x0,y0)$是$f^{\prime }(x，y)=0$的一个临界点，即$f_x(x_0,y_0)=0$ && $f_y(x_0,y_0)=0$，

（2）多元函数求极值：对于二阶连续函数$f(x_1,x_2,\dots ,x_n)$：

Hessian矩阵是一个多元函数的二阶偏导数构成的方阵，描述了函数的局部曲率。例如对于上面的多元函数，如果它的二阶偏导数都存在，那么Hessian矩阵如下:

根据Hessian矩阵，我们就可以判断上述极值的3种情况了，结论如下
（a）如果Hessian矩阵是正定矩阵，则临界点处是一个局部极小值；
（b）如果Hessian矩阵是负定矩阵，则临界点处是一个局部极大值；
（c）如果Hessian矩阵是不定矩阵，则临界点处不是极值。

对于上述多元函数求极值中的：

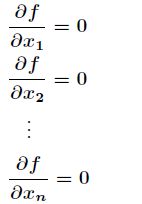
首先要求解该方程的解，才能进一步求极值。求解该方程的解采用牛顿迭代法，如下文所述。

牛顿迭代法

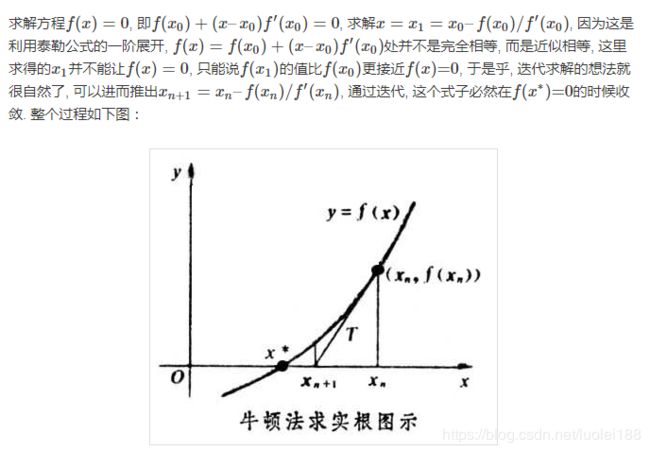
牛顿迭代法原理是利用泰勒公式。
对于方程 $f^{\prime }(x)=0$：在$x_0$处展开, 且展开到一阶, 即

对于多元函数求解方程，令$X=[x_1,x_2,\dots ,x_n{]}^T$，有：

其中，$J_f(X)$为雅各比矩阵：

采用牛顿迭代法求解非线性方程组的结果，牛顿迭代法不一定收敛，因此不一定能求得出解。具体牛顿迭代法不收敛问题，请见其他帖子。

（首篇博客，多有不足之处还请见谅！）

by 三石の四夕
2018/11/11