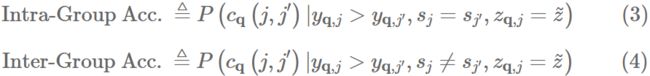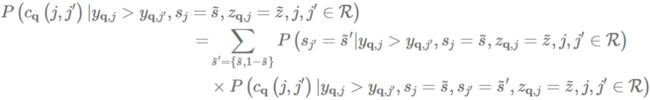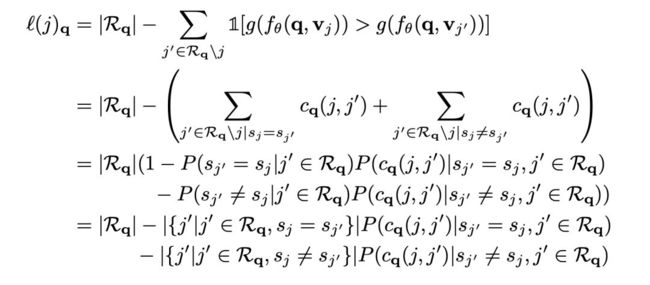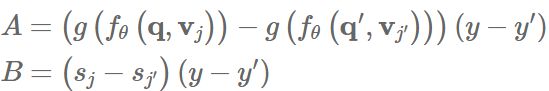Google 推荐系统公平性论文解读
作者:王鸣辉
整理:Hoh Xil
来源:http://wd1900.github.io/#blog
https://www.zhihu.com/people/wang-ming-hui-38/posts
导读:今天分享的是谷歌一篇关于推荐系统中公平性的文章。
Fairness in Recommendation Ranking through Pairwise Comparisons
https://arxiv.org/pdf/1903.00780.pdf
我之前也没有太关注这一块的工作,这次和大家一起解读一下,希望能为以后的工作提供些启发。
推荐系统现在可以说是无处不在,那么有时候我们就需要考虑公平性的问题:
什么是公平性?
如何量化它?
如何解决它?
文章提供了一些指标来评价推荐系统算法的公平性,并展示了如何基于随机化实验的 pairwise comparisons 来衡量公平性。根据相应指标,提出了一个新的正则化方法,来促使模型在训练中改进相应指标,从而提高排序的公平性。将这种 pairwise 正则化应用于一个大规模的生产环境推荐系统后,能够显著提高系统的 pairwise fairness,同时保证相应的点击与互动指标不掉。
总的来说,虽然提升公平性的过程中,点击和互动指标是中性的。也是说从用户侧实验角度来说其实是没有提升的,实际工作中遇到这种情况其实是无法推上线的。不过我觉得有打算在线上尝试的同学可以考虑开开作者侧实验,文章中的结论显示对于原先学习不充分的 group,在应用 pairwise 正则化后,可以提高其点击率,也就会增加其曝光机会,在不影响大盘指标的情况下,我觉得这个对于作者的发文尤其是小众的,应该是正向的。
依旧收简历,欢迎各位同学来抖音火山推荐团队,邮箱:
▌Introduction
本文聚焦于推荐系统中 under-ranking groups of items 的风险。例如,如果社交网络对某个人口统计群体的帖子排名不高,那就可能会限制该群组在服务中的可见性。
现在研究人员已经提出了很多关于公平性的指标,研究推荐系统中公平性的一个挑战就是指标很复杂。它们通常由多个模型组成,必须平衡多个目标,并且由于极端和倾斜的稀疏性而难以评估。所有这些问题在推荐系统社区中很难解决,并且在改进推荐公平性上存在着额外的挑战。
另一个挑战是将推荐系统当做 pointwise 预测问题,然后应用到排序列表中。实际排序构建与 pointwise 是有个 gap 的。公平性问题也有类似的困境。现在研究的公平性指标多围绕于 pointwise 准确性,但这并不意味着用户最终看到的排序就好。
另外,因为系统一直在动态变化,所以推荐系统的评估是及其困难的。用户昨天感兴趣的,明天就可能不感兴趣了,我们只有在向他们推荐 item 时才知道他们是否真的感兴趣。这就导致通过之前推荐系统得到的指标是有偏的,有大量的研究工作是去做一个无偏的离线评估,但因为巨大的 item space、反馈的稀疏性以及不断变化的 user 和 item,使其变得很困难。
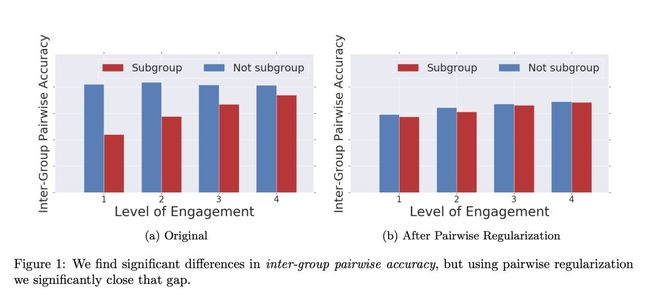
本文通过一个 pairwise recommendation fairness metric 来解决这些挑战。用容易的随机实验去获取用户偏好的无偏估计。基于这些 pairwise preference,我们也能测量一个 pointwise 推荐系统的公平性,并表明这些指标与排序效果直接相关。此外,我们提供了一种新颖的正规化项,可以提高 pointwise 推荐的最终排序的公平性,如图1所示。我们在生产环境的大规模推荐系统上进行测试,并显示出实际的收益,并进行理论&经验上的权衡。
总的来说,文章有以下贡献:
Pairwise Fairness: 基于 pairwise 提出一系列新颖的评估推荐公平性的指标,并表明 pairwise fairness metric 与排序效果直接相关并分析与 poinwise fairness metrics 的关系。
Pairwise Regularization: 提出一个正则化方法在给定的指标上提高模型性能,同时对 pointwise 模型也有效。
Real-world Experiments: 在大规模生产环境的推荐系统上实验,论证其在 pairwise fairness 上有显著提升。
▌Related Work
Recommender Systems.
Machine Learning Fairness.
Recommender System Fairness.
Fairness Optimization.
▌Pairwise Fairness for Recommendation
1. Recommendation Environment
假定一个给用户推荐个性化 top-K items 的生产环境推荐系统,一个带一组检索系统+排序系统的级联推荐。我们假定检索系统从总候选 J 里 M 个 items 里,筛出 M’ 个 items 的集合 R,其中 M >> M’ >= K。排序模型对 M 个 items 打分,然后返回 top-K 个 items,这里我们聚焦于排序模块。
细节不太讲了,排序这块就是基于各种目标如点击,时长,购买等进行建模。本系统会评估用户是否点击 ![]() ,以及用户点击后的 user engagement
,以及用户点击后的 user engagement ![]() ,比如停留时长,购买或者打分等交互指标。
,比如停留时长,购买或者打分等交互指标。
ranker 是以 θ 为参数的模型 fθ;训练模型以预测 user engagement:
最后,通过单调评分函数 ![]() 产生最终排序,并且向用户显示 top-K 个items。
产生最终排序,并且向用户显示 top-K 个items。
2. Motivating Fairness Concerns
本文聚焦于 under-recommended 的 groups of items 的风险。比如,一个社交网络会将 a given demographic group 排得靠后,那么可能会限制该群组的可见度和参与度。如果一个网站的评论模块是个性化的,如果特定群体的评论排序靠后,那么他们将会在网站拥有更少的声音。更抽象的说,我们假设每个 item j 都有敏感属性 ![]() 。我们会去评测是否一个 group 的 items 被系统性地排后。
。我们会去评测是否一个 group 的 items 被系统性地排后。
虽然不是我们的主要关注点,但如果特定用户组偏好某一组项目,这些问题可能会与用户组问题保持一致。可以明确扩展此框架以合并用户组。如果每个用户都有敏感属性,我们可以计算每个用户组的所有以下指标,并比较各组之间的性能。例如,如果我们担心社交网络对特定人群的特定主题的项目排名不足,我们可以比较该主题的内容在特定人群中的排名不足的程度。
3. Pairwise Fairness Metric
尽管上边的目标看起来是 ok 的,但是我们必须更准确的去评判一个 item 是否是 "under-ranked"。
在这里,我们借鉴了 Hardt et al. [23] 对于平等赔率的理解,分类器的公平性。
通过比较其 FPR and/or FNR 来量化。换句话说,一个 item 是正的,分类器预测其为正的概率。这在分类问题是好用的,因为模型可以和一个预定的阈值比较。
在推荐系统中,什么是正确的预测是不太清晰的,即使我们忽略交互,将分析现在在点击上。比如一个 item 被点击,那么 y = 1,预测的概率 y_hat = 0.6,它是正确的预测吗?它可以被认为还差0.4,但相比于其他概率小于0.6的,它是排在前面的。因此要想了解 pointwise 的误差,需要在同一个 query 下比较 items 的预测状况。
我们定义一个 pairwise accuracy:对于同一个 query,被点击 item 排名高于未点击 item 的概率:
![]()
为了方便:
和大多数公平性研究一样,我们需要关注的其实是 cross group 的相对表现而非绝对值。
我们可以比较:
![]()
也就是一个 S = 0的 group 里 items 的 PairwiseAccuracy 是高于还是低于另一个 S = 1 的 group。
虽然这是一个很直观的 metric,但它的问题在于它完全忽略了用户 engagement z,可能会引发一些标题党之类的问题。所以要引入其他相关指标。
Definition 1 (Pairwise Fairness). 对于使用排序公式 g 的模型 f,如果在 items 被交互程度相同的情况下,其两个 group 里点击的 item 排在另一个未点击 item 之前的可能性在是相同的,则被认为满足 pairwise fairness:
![]()
此定义为我们提供了每个组中 items 的排名准确性的总体概念。
但这块对于曝光不足 group 的 items 还是有问题的。假设有 A、B 两个 group 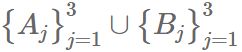 ,都有3个 items,第一种情况 A1 被点击,第二种 B1 被点击。
,都有3个 items,第一种情况 A1 被点击,第二种 B1 被点击。
第一种情况,系统给出 [A2,A3,B1,A1,B2,B3],第二种情况给出 [A1,A2,A3,B1,B2,B3],我们可以看到整体 pairwise accuracy 都是2/5,但是第二种情况,B 都在 A 后边。这个两个情况都有把被点击 item 排低的问题,但是后者显然更有问题,它独立于用户偏好,而系统性地偏好一个 group。
为了解决这个问题,我们将上述的 pairwise fairness 定义拆分成两个独立的标准:pairwise accuracy between items in the same group and pairwise accuracy between items from different groups。我们将这些 metrics 叫做intra-group pairwise accuracyandinter-group pairwise accuracy
于是我们也可以定义 Intra-Group Pairswise Fairness and Inter-Group Pairwise Fairness 标准。
Definition 2 (Intra-Group Pairwise Fairness). 对于使用排序公式 g 的模型 f,如果在 items 被交互程度相同的情况下,两个 group 里内部点击的 item 排在另一个未点击 item 之前的可能性在是相同的,则被认为满足 intra-group pairwise fairness:
![]()
Definition 3 (Inter-Group Pairwise Fairness). 对于使用排序公式 g 的模型 f,如果在 items 被交互程度相同的情况下,两个 group 里点击的 item 排在另一个组里未点击 item 之前的可能性在是相同的,则被认为满足 inter-group pairwise fairness:
说的有点啰嗦,公式其实比较清晰。
在某种程度上的组内公平性与整体公平概念起类似作用,因为它表示推荐系统能够很好地对用户感兴趣的项目进行排名。组间公平性则让我们进一步了解以 group 为整体中,排序中错误的代价。
通过分解整体 pairwise accuracy,我们可以看得更清晰:
也就是说,我们发现我们可以将 pairwise comparisons 分为两组,即组内和组间比较,并且 overall pairwise accuracy 是 inter-group accuracy 和 intra-group accuracy 的加权和,其中权重通过相应的点击和参与度的概率来确定。这些指标使我们更好地了解推荐系统的公平性。
4. Measurement
如开头所说,推荐系统中的 user 和 item 是动态的,并且我们通常仅能观察到用户对先前推荐的项目的反馈,这使得指标易受先前推荐系统中的偏差影响。
但是,对于上面给出的所有三个公平性定义,我们希望对 items pair 之间的用户偏好进行无偏估计。为此,我们在推荐系统上一小部分 query 进行 randomized experiments。下面的实验描述都假设在实验组中对 query 子集进行操作。
对于实验的 query,我们将在推荐位置2和3向用户展示一对 items;这可以防止位置偏差,即排名低的项目比排名高的项目更不可能被点击。因为上面的定义是来自给定 query 的相关项集合的任意项目对,所以对于每个 query,从 Rq 随机选择两个项目,那它们在位置二和三中的排序也是随机的。
在实验 query 中,只有一小部分将对随机项目对中的一个项目进行点击。当有 item 被点击时,我们记录 query,pair,被点击 item 后续的 engagement z。有了这个,我们可以计算上面公平性定义中的所有概率。在实践中,我们将 z 离散化为桶以便于比较。
请注意,通过此实验可以看出,如果 item 未被点击,我们将无法观察到参与度。这使我们当前的指标设计基于 z 的条件,而不是估计 z 的准确性,因为我们只知道该 pair 中被点击 item 的 z。
Discussion 这些指标将排序模型的性能与最终排序的最终公平性属性联系起来。一个潜在的假设是,相关项目集合 Rq 的检索系统在某种意义上是“公平的”。我们认为需要进一步的研究来理解检索系统对“公平”的意义以及检索系统中的任何程度的偏差如何通过排名系统传播来影响最终的排序体验。
▌Theoretical Analysis
1. Ranking Interpretation
目前描述的指标主要是类似 pairwise accuracy,但也可以从 ranking 的角度来解释。一个推荐系统通过 g 和 fθ 来对 ![]() 进行排序。用
进行排序。用 ![]() 来表示 item j 在排序 list 中的位置:
来表示 item j 在排序 list 中的位置:
上式其实就把 pairwise fairness 和排序位置的公平性联系了起来。
Theorem 1. 如果一个推荐系统达到 pairwise fairness,那么组间 engagement 为 z 的 clicked item 的预期位置是相同的。
Proof. This falls out of the definition of pairwise accuracy and pairwise fairness:
因此,我们可以将 pairwise recommender fairness 解释为被点击和交互 item 的位置不应取决于组内成员的平均值。(这种分析类似于传统 pairwise IR 中的概率解释,但现在是在推荐系统公平性的背景下。)
inter-group and intra-group pairwise accuracies 也和 clicked item 的排序位置相关联。
这里整体排名可以被分解为来自同一组的排名和来自其他组的排名。但是,由于每种类型的比较数量可能会有不同的分布,我们认为将这些术语作为概率是有意义的。
2. Relation to Pointwise Metrics
推荐系统中经常会根据 Calibration 和 RMSE 进行评估,这些指标对于分类和推荐来说是重要的公平性指标,但是对于保证 pairwise fairness 还是不足的。
举个简单的例子,![]() ,可以被认为是用 pCTR 来排序,对于每个 group s,用
,可以被认为是用 pCTR 来排序,对于每个 group s,用 ![]() 来表示其 label y 的均值。
来表示其 label y 的均值。
Calibration 先看一下 calibration 和 pairwise fairness 之间的关系,一个 pCTR 模型 f(x),当且仅当 y 满足以下情况,可以认为是校准的。
就是预测值的均值等于实际均值,可以大概理解为在全局上是准的。
Lemma 1. A calibrated model is insufficient for guaranteeing pairwise ranking fairness.
Proof. 举个 calibrated model 不满足 pairwise fairness 的例子,假设我们学到一个模型对任意 group s 的 item 可以预测 ![]() 。这个模型毫无疑问是对每个 group 都校准了。
。这个模型毫无疑问是对每个 group 都校准了。
如果我们有两个组,![]() 和
和 ![]() ,
,![]() ,对任意 items j 属于
,对任意 items j 属于 ![]() ,和 j’ 属于
,和 j’ 属于 ![]() ,有
,有 ![]() 。因此
。因此
and
显然没有保证组间的公平性。根据公式(7),我们可以发现只要
全局 pairwise fairness 的公平性就无法保证。
Squared Error 推荐系统中另一个通用指标就是MSE,此指标和其变种被用来评估协同过滤系统的公平性。虽然可能促进跨群体间的准确性,但是还是不足以保证pairwise fairness。
Lemma 2. Equal MSE across groups is insufficient for guaranteeing pairwise ranking fairness.
Proof. 还是举个满足跨组MSE的模型,但不满足 pairwise fairness。和刚才一样,学到模型 ![]() 。同样两个 group,有
。同样两个 group,有 ![]() and
and ![]() ,可以看到:
,可以看到:
and
也无法保证组间的公平性。
跨组的 MSE 直观上是有价值的,但是如前文所写,其对排序是不足的,MSE 没有区分过度预测和预测不足,不过即使考虑到也还是没用,因为其忽略了相对排名。
3. Pairwise Regularization to Improve Fairness
如何学到一个推荐系统让其满足公平性呢?之前说过,目前生产环境上的推荐系统大多是 pointwise 的,去预测 y 和 z,所以我们提出一种建模方法且适用于现存技术。
进一步,我们假设已知 ![]() 并且其是可微的,因此我们用一下目标训练模型 fθ:
并且其是可微的,因此我们用一下目标训练模型 fθ:
D 是原始训练数据,P 是前文说的实验数据由 ![]() 组成。第二项是由 A B 计算来的相关性,都是来自 P 的随机变量。
组成。第二项是由 A B 计算来的相关性,都是来自 P 的随机变量。
pairwise regularizer 会计算被点击和未被点击的项目之间的残差与被点击的项目的组成员的相关性。因此,如果模型预测某个组里项目被点击的能力优于另一个组,则该模型会受到惩罚。
为保证有足够的数据进行有意义的计算,重新平衡了下 P,让其有一半的被点击的 item 属于 group s = 0,另一半属于 group s = 1。根据目标我们可以进行更进一步的限制,如果我们关注组内公平,那么我们可以限制 P 让 ![]()
这种方法既适用于 pointwise 推荐系统,也适合 pairwise 推荐系统。
其不能证明能保证 pairwise fairness,但是它有很强的实验效果并且易于应用,这对生产环境很重要。
▌Experiments
为了理解 pairwise fairness 指标和提出的建模改进,我们研究了大规模生产环境推荐系统的效果。分析 sota 模型的性能以及我们的建模更改对系统的影响。
1. Experimental Setup
如前文,这是一个多个检索系统+排序模型的级联推荐系统。我们评估的是排序效果。排序模型是一个 muti-head 的多层 NN 模型,预测点击 y 和后续转化的交互 z,模型持续得由之前推荐的数据去训练。这算是目前业界标配的搞法了。
我们研究了排序模型对于 sensitive subgroup 相对于其他数据 “not subgroup” 的效果。subgroup 大概占了总 items 的0.2%,但其对于分析推荐系统公平性很重要。如之前随机试验所述,我们收集向用户展示的相关 items 的随机对数据集 P,并在用户点击其中一个项目时进行记录。我们从数据集中随机取一半用于 pairwise regularization,另一半用于评估模型。
比较两个版本的模型:
(1) 不考虑任何公平性的生产模型
(2) 同样结构但是用 pairwise regularization 去优化组间 pairwise 公平性的测试模型。
如下所示,我们聚焦于组间公平性,因为这块更待提高。
因为敏感性,这里就不写绝对指标了,而是 subgroup 和其余项的相对效果。简单汇总平均了不同交互级别的 pairwise accuracy,并通过 not subgroup 的平均准确率除以 subgroup 得到相对准确率。所有绘图将 engagement z 分为四个级别并保持相同的 y 轴缩放,以便比较。
2. Baseline Performance
(1) pairwise fairness
(2) intra-group pairwise fairness
(3) inter-group pairwise fairness
图2(a)可以看到,engagement 低的时候,subgroup 的 items 是 under-rank,当 engagement 高时是 over-rank。总体来说 non-subgroup 略优8.3%。
图3(a)显示 subgroup 在任意级别的 engagement,选被点击 item 的效果更困难。non-subgroup 在 intra-group pairwise fairness 上优 14.9%。这部分是由于 subgroup 很小,而 non-subgroup 项目之间存在更多的差异,使得比较更容易。当移除 subgroup 里很多高相似的,性能就没有区别了。
因为发现组间公平性很差,non-subgroup 优35.6%,所以我们聚焦提升组间 pairwise fairness。
3. Fairness Improvements
图一显示 pairwise regularization 基本使组间公平性对齐,正则化让 non-subgroup 的 pairwise accuracy 下降了,使两组间的差距从35.6%下降到2.6%,但是 non-subgroup 的精度下降是不好的,不过测试模型的 pairwise accuracy 还是和之前组间看到的 pairwise accuracy 大致相当。
图2可以看到组间效果是提升的,差别从8.3%降到2.5%,但是 Intra-group accuracy 基本没被 pairwise regularization 优化。
在线上实验中,我们发现对于 engagement 指标是中性的,subgroup 在全局中也只是很小的一部分,取得公平性收益并没有以全局效果为代价。
4. How are improvements achieved?
结果可靠,但我们进一步进行分析,来了解正规化如何缩小 fairness gaps。我们检查每组 item 的 exposure 和用户偏好的比较,类似于粗略的 pairwise 校准分析。
图4(a)显示,不论什么级别的 engament,subgroup 的点击率一直比较差,但是高 engagement 的 item 相对点击率到还好。
exposure:模型将一组 item 排到另一组 item 上的概率
图4(c)中展现了正则项 subgroup 的 item 有更高的点击率相对于自然学习来说,这也就给了 subgroup item 更多的被推荐机会。
▌Conclusion
这项工作提供了一种易于理解的方式来获得推荐系统排序公平性的无偏差测量,通过成对实验来观察用户偏好来做到。基于这些实验数据,可以评估和分解推荐系统的公平性,以查看模型是否系统地对特定组中的项目进行错误排序或排名不足。我们证明这一指标与排序平性定义一致,但不包括 pointwise 公平性指标。我们最终提出了一种新颖的 pairwise regularization 方法,以提训练期间推荐系统的公平性,并表明它显著提高了大规模生产系统中的公平指标。
「 更多干货,更多收获 」
![]()
推荐系统教程之十:协同过滤中的相似度计算方法有哪些?
智能推荐系统的终极目标:“让你成为更好的自己”
【推荐算法】基于用户和产品的协同过滤推荐算法
【分享】推荐时代的内容理解技术探索.pdf(附下载链接)
今日头条推荐系统原理
feed流设计:那些谋杀你时间的APP
如何搭建一套个性化推荐系统
从零开始搭建创业公司后台技术栈
关注我们
智能推荐 个性化推荐技术与产品社区 |
长按并识别关注
|
一个「在看」,一段时光!?