快速傅里叶变换(FFT)和小波分析在信号处理上的应用
1前言
1.1傅里叶变换
函数f(t)为一元连续函数,其傅里叶变换定义为:
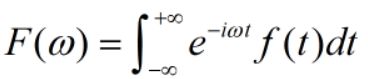
F(w)的傅里叶逆变换定义为:
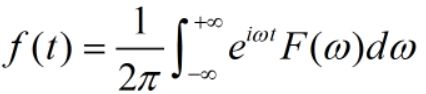
其中,i为虚数单位。由欧拉公式:
![]()
任意绝对可积的连续函数f(t),都可以用三角函数表示,由于三角函数是周期函数,由此可展开为傅里叶级数。本文不加证明地给出傅里叶级数展开式:
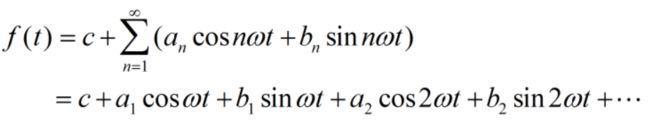
设F是所有由一元连续的绝对可积的函数组成的空间,由傅里叶级数知
![]()
是F的一组基,即对任意的f(t)属于F,都可以用这组基表示。
实际上,cos(0wt)=1,sin(0wt)=0,但是由于0乘任何数都等于0,不能作为基。这就将基都是由三角函数组成统一起来了。
对任意f(t)、g(t)属于F,定义内积如下:
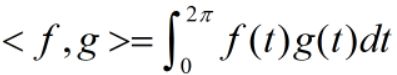
由此,对任意f(t)、g(t)属于B,有
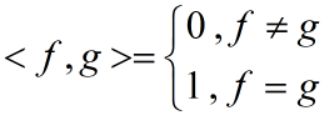
所以,B是F的一组标准正交基。对任意f(t)属于F,由内积导出范数:
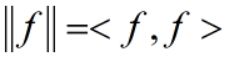
在《泛函分析》中,已证明F为完备的赋范线性空间,进一步可得,F为希尔伯特(Hibert)空间。
那么,如何求一个函数f(t)的傅里叶展开式?这时,傅里叶变换就派上用场了。
设f(t)的傅里叶展开式如下:
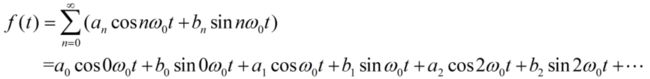
假设已经求得f(t)的傅里叶变换函数F(w),如何利用F(w)求得a_m,b_m(m=0,1,2,…)?
实际上a_m,b_m分别是F(mw_0t)的实部(a)和虚部的相反数(-b),即:
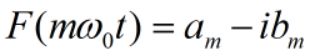
证明如下:

其实,傅里叶变换的作用不仅限于此,在求解微分方程时,能够将复杂的积分运算转换成简单的线性运算。对微分方程两边同时进行傅里叶变换,原微分方程就转化为普通一元方程,求出一元方程的解后,再进行傅里叶逆变换,就得到原微分方程的解。读者若对傅里叶级数很感兴趣,请参见《复变函数》。
在信号处理中,傅里叶级数又扮演着什么样的角色?在工程应用中,信号函数f(t)一般极其复杂,往往还夹杂着噪声,无法通过函数图像看出其包含的基本波形频率及振幅。设信号f(t)的傅里叶展开式为:
![]()
通过辅助角公式:
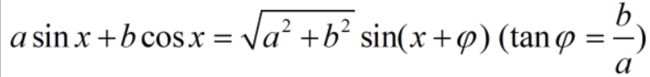
f(t)可以转化为如下形式:
![]()
可以看出频率和振幅信息。其中nw为频率,c_n为振幅,反映了波的能量大小。当c_n比较小时,说明该频率的波能量较小,可认为是噪声波,去掉该项,再将留下来的波进行重构,起到去噪作用。如果以nw为横坐标,c_n为纵坐标,信号f(t)的信息又可用一串(nw,c_n)点表示,由此得到频谱图。即将时域信息转换为频域信息。
1.2小波分析
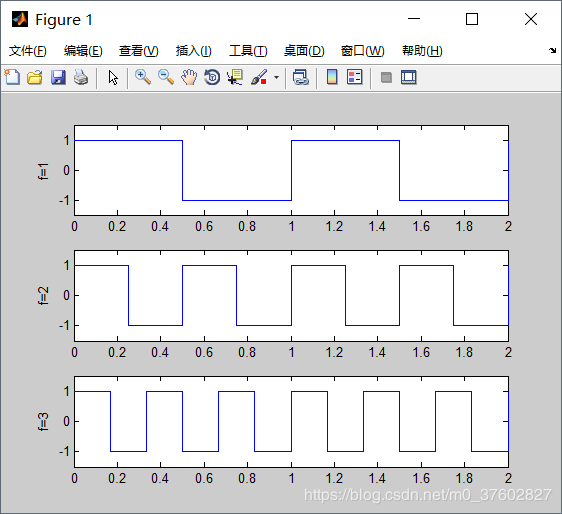
小波分析在FFT的基础上,将波形进行改进。FFT以正玄波为母波(余弦波可通过正弦波移相得到),通过增大频率得到一列子波,来建立一组基。小波分析采用更加灵活的波形。如下图,如果1号波的频率为1,那么2号和3号波的频率分别为2、4。
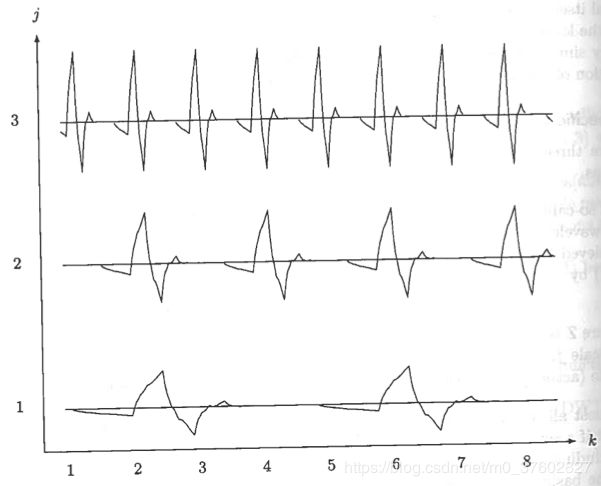
常用的小波如下:
(1)RbioNr.Nd小波(reverse双正交小波)
(2)Gaus小波(由高斯函数派生出)
(3)Dmey小波(Meyer函数的近似,能快速进行小波变换)
(4)Cgau小波(复数形式的高斯小波)
(5)Cmor小波(复数形式的morlet小波)
(6)Fbsp小波(复频域B样条小波)
2信号信息
本文以频率和振幅分别f1=5Hz、a1=6,f2=15Hz、a2=3的两列波为理想信号,以0均值、振幅不超过4的随机扰乱信号为噪声波,两者叠加得到实际波。代码如下:
clear,clc
N=300; %信号采样个数(300个)
F=1000; %采样频率(1000Hz)
t=linspace(0,0.3,N); %时间向量,0.3s采样300个样本,采样频率为1000Hz
%%%%%%%%%%%%%%%%%%%%1.波信号信息%%%%%%%%%%%%%%%%%%%%
x=6*sin(2*pi*5*t)+3*sin(2*pi*15*t); %理想信号(f1=5Hz,a1=6;f2=15Hz,a2=3)
y=4*(rand(1,N)-0.5); %噪声信号(0均值随机扰动)
z=x+y; %实际信号
figure
subplot(221)
plot(t,x);
xlim([0 0.3])
title('理想信号');
subplot(222)
plot(t,y);
xlim([0 0.3])
title('噪声信号');
subplot(223)
plot(t,z);
xlim([0 0.3])
title('实际信号');
subplot(224)
plot(t,x,'linewidth',3.0); %加粗曲线
xlim([0 0.3])
hold on
plot(t,z,'--r')
title('理想信号与实际信号');
3应用快速傅里叶变换(FFT)获取信号频谱图
频谱图,即振幅与频率的关系图。由傅里叶展开式:
![]()
傅里叶展开式每一项前面的系数ci为频谱图的纵轴,每一项内部的系数wn为横轴。代码如下:
%%%%%%%%%%%%%%%%%%%%2.应用FFT(快速傅里叶变换)获取信号频谱图%%%%%%%%%%%%%%%%%%%%
n=2^nextpow2(N); %参加FFT的采样点个数为512(300后面的2的指数函数值)
fly=fft(z,n); %对原始信号进行离散傅里叶变换
a=abs(2*fly/N); %振幅
f=F/2*linspace(0,1,n/2+1); %频率
figure
plot(f(1:80),a(1:80)); %绘制信号频谱图
title('频谱图');
xlabel('频率');
ylabel('振幅');
运行结果:
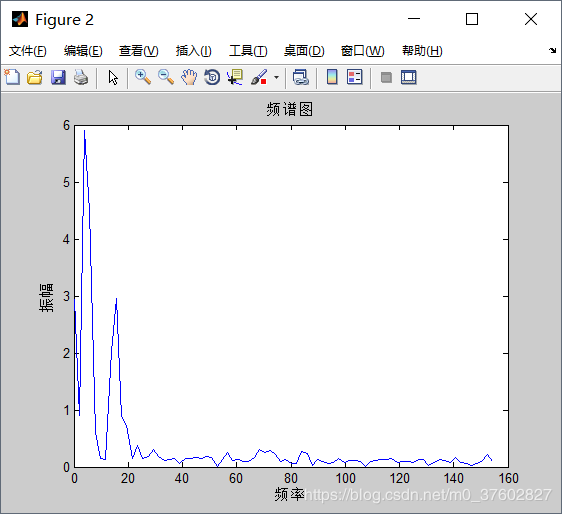
曲线和横轴围成的面积反应了波的能量。从上图可以看出,振幅和频率分别为f1=5Hz、a1=6,f2=15Hz、a2=3的两列波附近的能量比较高,可认为是有效信号,而其他波形附近的能量都比较弱,可认为是噪声。
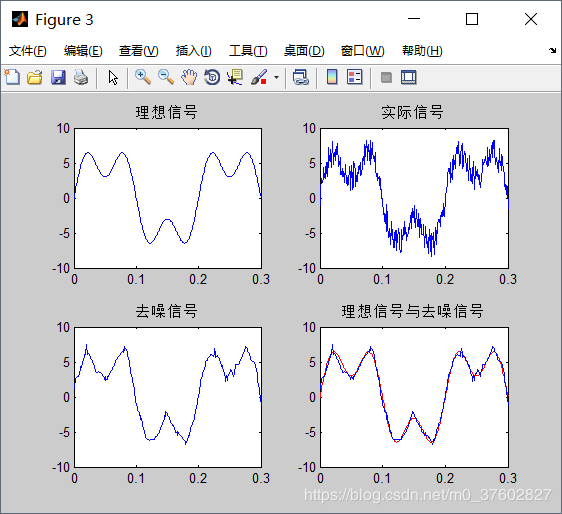
4应用小波分析进行去噪处理
删除信号f(t)傅里叶展开式中振幅ci较小的波,将留下来的波进行波形重构,就达到去噪目的。代码如下:
%%%%%%%%%%%%%%%%%%%%3.应用小波分析进行去噪处理%%%%%%%%%%%%%%%%%%%%
xb=wden(z,'minimaxi','s','one',4,'db3');
figure
subplot(221)
plot(t,x);
xlim([0 0.3])
title('理想信号');
subplot(222)
plot(t,z);
xlim([0 0.3])
title('实际信号');
subplot(223)
plot(t,xb);
xlim([0 0.3])
title('去噪信号');
subplot(224)
plot(t,x,'r',t,xb);
xlim([0 0.3])
title('理想信号与去噪信号');
5应用小波分析进行信号压缩
曲线的信息量远比直线的信息量高,若以硬极核函数为小波,就可对原信号进行压缩。
代码如下:
%%%%%%%%%%%%%%%%%%%%4.应用小波分析进行信号压缩%%%%%%%%%%%%%%%%%%%%
figure
subplot(321);
plot(t,z);
xlim([0 0.3])
title('实际信号');
alpha=1.4;
for i=1:5
[C,L]=wavedec(x,i,'haar'); %使用haar小波对信号进行i层分解
thr=wdcbm(C,L,alpha); %获取信号压缩的阈值(threshold)
xd=wdencmp('lvd',C,L,'haar',i,thr,'s'); %对信号进行压缩
subplot(3,2,i+1);
plot(t,xd);
xlim([0 0.3])
ylabel([num2str(i),'层分解']);
end
运行结果:
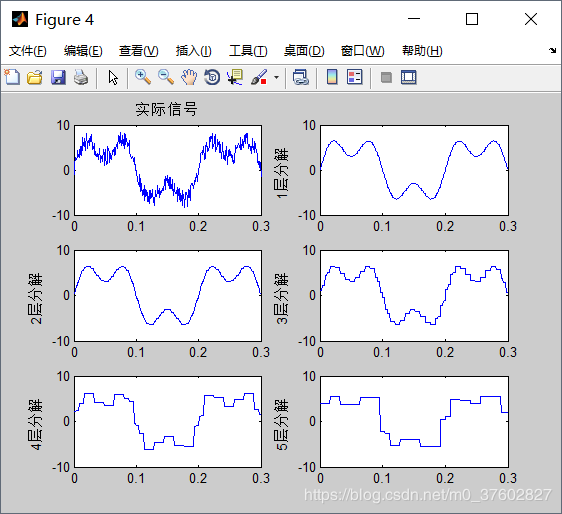
可以看到,压缩后的信号中有明显的线段。好比同一张照片,若降低像素,可以看到明显的格点。
6应用小波分析进行信号分离
代码如下:
%%%%%%%%%%%%%%%%%%%%5.应用小波分析进行信号分离%%%%%%%%%%%%%%%%%%%%
[C,L]=wavedec(z,5,'db5'); %使用db5小波对信号进行5层分解
figure;
subplot(321);
plot(t,z);
xlim([0 0.3])
ylabel('实际信号');
for i=1:5
%对分解的第5层到第1层的低频系数进行重构
A=wrcoef('A',C,L,'db5',6-i);
subplot(3,2,i+1);
plot(t,A);
xlim([0 0.3])
ylabel(['A',num2str(6-i)]);
end
figure;
subplot(321);
plot(t,z);
xlim([0 0.3])
ylabel('实际信号');
for i=1:5
% 对分解的第5层到第1层的高频系数进行重构
D=wrcoef('D',C,L,'db5',6-i);
subplot(3,2,i+1);
plot(t,D);
xlim([0 0.3])
ylabel(['D',num2str(6-i)]);
end
运行结果:
(1)对分解的第5层到第1层的低频系数进行重构
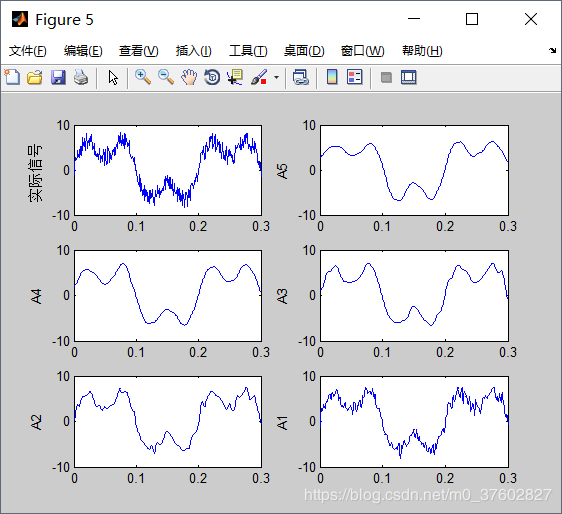
本例的理想信号的两列波的频率分别为f1=5Hz、f2=15Hz,都属于低频波,所以重构效果较好。
(2)对分解的第5层到第1层的高频系数进行重构
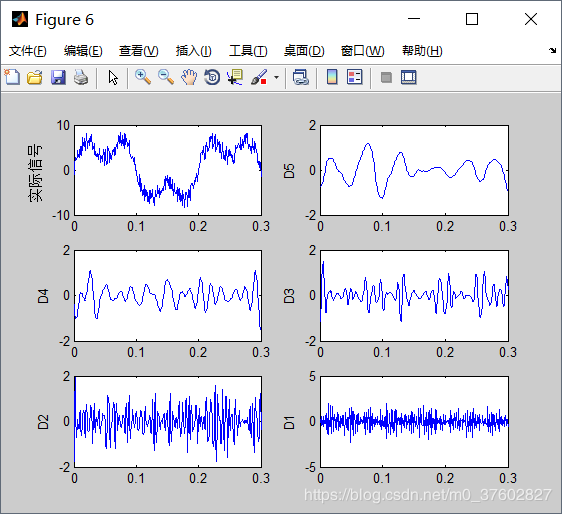
本例的理想信号的两列波的频率都属于低频波,而高频波主要是噪音,所以重构效果较差。
7全部代码
clear,clc
N=300; %信号采样个数(300个)
F=1000; %采样频率(1000Hz)
t=linspace(0,0.3,N); %时间向量,0.3s采样300个样本,采样频率为1000Hz
%%%%%%%%%%%%%%%%%%%%1.波信号信息%%%%%%%%%%%%%%%%%%%%
x=6*sin(2*pi*5*t)+3*sin(2*pi*15*t); %理想信号(f1=5Hz,a1=6;f2=15Hz,a2=3)
y=4*(rand(1,N)-0.5); %噪声信号(0均值随机扰动)
z=x+y; %实际信号
figure
subplot(221)
plot(t,x);
xlim([0 0.3])
title('理想信号');
subplot(222)
plot(t,y);
xlim([0 0.3])
title('噪声信号');
subplot(223)
plot(t,z);
xlim([0 0.3])
title('实际信号');
subplot(224)
plot(t,x,'linewidth',3.0); %加粗曲线
xlim([0 0.3])
hold on
plot(t,z,'--r')
title('理想信号与实际信号');
%%%%%%%%%%%%%%%%%%%%2.应用FFT(快速傅里叶变换)获取信号频谱图%%%%%%%%%%%%%%%%%%%%
n=2^nextpow2(N); %参加FFT的采样点个数为512(300后面的2的指数函数值)
fly=fft(z,n); %对原始信号进行离散傅里叶变换
a=abs(2*fly/N); %振幅
f=F/2*linspace(0,1,n/2+1); %频率
figure
plot(f(1:80),a(1:80)); %绘制信号频谱图
title('频谱图');
xlabel('频率');
ylabel('振幅');
%%%%%%%%%%%%%%%%%%%%3.应用小波分析进行去噪处理%%%%%%%%%%%%%%%%%%%%
xb=wden(z,'minimaxi','s','one',4,'db3');
figure
subplot(221)
plot(t,x);
xlim([0 0.3])
title('理想信号');
subplot(222)
plot(t,z);
xlim([0 0.3])
title('实际信号');
subplot(223)
plot(t,xb);
xlim([0 0.3])
title('去噪信号');
subplot(224)
plot(t,x,'r',t,xb);
xlim([0 0.3])
title('理想信号与去噪信号');
%%%%%%%%%%%%%%%%%%%%4.应用小波分析进行信号压缩%%%%%%%%%%%%%%%%%%%%
figure
subplot(321);
plot(t,z);
xlim([0 0.3])
title('实际信号');
alpha=1.4;
for i=1:5
[C,L]=wavedec(x,i,'haar'); %使用haar小波对信号进行i层分解
thr=wdcbm(C,L,alpha); %获取信号压缩的阈值(threshold)
xd=wdencmp('lvd',C,L,'haar',i,thr,'s'); %对信号进行压缩
subplot(3,2,i+1);
plot(t,xd);
xlim([0 0.3])
ylabel([num2str(i),'层分解']);
end
%%%%%%%%%%%%%%%%%%%%5.应用小波分析进行信号分离%%%%%%%%%%%%%%%%%%%%
[C,L]=wavedec(z,5,'db5'); %使用db5小波对信号进行5层分解
figure;
subplot(321);
plot(t,z);
xlim([0 0.3])
ylabel('实际信号');
for i=1:5
%对分解的第5层到第1层的低频系数进行重构
A=wrcoef('A',C,L,'db5',6-i);
subplot(3,2,i+1);
plot(t,A);
xlim([0 0.3])
ylabel(['A',num2str(6-i)]);
end
figure;
subplot(321);
plot(t,z);
xlim([0 0.3])
ylabel('实际信号');
for i=1:5
% 对分解的第5层到第1层的高频系数进行重构
D=wrcoef('D',C,L,'db5',6-i);
subplot(3,2,i+1);
plot(t,D);
xlim([0 0.3])
ylabel(['D',num2str(6-i)]);
end
8参考链接
[1] 傅里叶分析之掐死教程(完整版)
[2]【小波分析(一)】
[3]【傅里叶展开式】
[4]【小波变换】