机器学习中的梯度下降算法（BGD，SGD，MBGD）

1. 前言

机器学习中常常将具体的问题抽象为数学表达，再通过最优化算法求取相关参数的最优值。其中最常用的便是基于梯度的优化算法。则可以将其总结为批量梯度下降法（BGD）、随机梯度下降法（SGD）、小批量梯度下降法（MBGD），本文也将从这几个方面进行解释。
首先，定义决策函数为：

yθ=∑i=1mθxi y θ = ∑ i = 1 m θ x i

则可以将损失函数定义为如下形式：

L(θ)=1m∑i=1m(yi−yθ(xi))2 L ( θ ) = 1 m ∑ i = 1 m ( y i − y θ ( x i ) ) 2

者就是求取最优值的问题，那么采用的算法一般为前面提到的方法。

2. 批量梯度下降法（BGD）

批量梯度下降法（Batch Gradient Descent，简称BGD）是梯度下降法最原始的形式，它的具体思路是在更新每一参数时都使用所有的样本来进行更新，其数学形式如下：
(1) 对上述的能量函数求偏导：

∂L(θ)∂θj=−1m∑i=1m(yi−yθ(xi))xji ∂ L ( θ ) ∂ θ j = − 1 m ∑ i = 1 m ( y i − y θ ( x i ) ) x i j

(2) 由于是最小化风险函数，所以按照每个参数θθ的梯度负方向来更新每个 θ θ ：

θ‘j=θj+1m∑i=1m(yi−yθ(xi))xji θ j ‘ = θ j + 1 m ∑ i = 1 m ( y i − y θ ( x i ) ) x i j

从上面公式可以注意到，它得到的是一个全局最优解，但是每迭代一步，都要用到训练集 所有的数据，如果样本数目 m m 很大，那么可想而知这种方法的迭代速度！所以，这就引入了另外一种方法，随机梯度下降。
优点：全局最优解；易于并行实现；
缺点：当样本数目很多时，训练过程会很慢。
下面是之前Softmax使用该下降算法得到的求解参数变化曲线：

3. 随机梯度下降法（SGD）

由于批量梯度下降法在更新每一个参数时，都需要所有的训练样本，所以训练过程会随着样本数量的加大而变得异常的缓慢(需要更多的迭代次数)。随机梯度下降法（Stochastic Gradient Descent，简称SGD）正是为了解决批量梯度下降法这一弊端而提出的。
将上面的损失函数写为如下形式：

L(θ)=1m∑i=1m(yi−yθ(xi))2=1m∑i=1mcost(θ,(xi,yi)) L ( θ ) = 1 m ∑ i = 1 m ( y i − y θ ( x i ) ) 2 = 1 m ∑ i = 1 m c o s t ( θ , ( x i , y i ) )

cost(θ,(xi,yi))=12(yi−yθ(xi))2 c o s t ( θ , ( x i , y i ) ) = 1 2 ( y i − y θ ( x i ) ) 2

利用每个样本的损失函数对θθ求偏导得到对应的梯度，来更新 θ θ ：

θ‘j=θj+(yi−yθ(xi))xji θ j ‘ = θ j + ( y i − y θ ( x i ) ) x i j

随机梯度下降是通过每个样本来迭代更新一次，如果样本量很大的情况（例如几十万），那么可能只用其中几万条或者几千条的样本，就已经将theta迭代到最优解了，对比上面的批量梯度下降，迭代一次需要用到十几万训练样本，一次迭代不可能最优，如果迭代10次的话就需要遍历训练样本10次。但是，SGD伴随的一个问题是噪音较BGD要多，使得SGD并不是每次迭代都向着整体最优化方向。
优点：训练速度快；
缺点：准确度下降，并不是全局最优；不易于并行实现。
下面是之前Softmax使用该下降算法得到的求解参数变化曲线，可以很明显看到曲线的震荡：

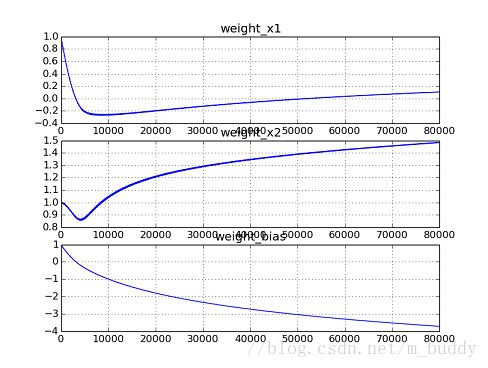
4. 小批量梯度下降法（MBGD）

有上述的两种梯度下降法可以看出，其各自均有优缺点，那么能不能在两种方法的性能之间取得一个折衷呢？即，算法的训练过程比较快，而且也要保证最终参数训练的准确率，而这正是小批量梯度下降法（Mini-batch Gradient Descent，简称MBGD）的初衷。
下面是之前Softmax使用该下降算法得到的求解参数变化曲线：

5. 总结

（1）BGD：使用全部的样本进行目标参数更新，空间消耗大
（2）SGD：每次使用1个样本进行目标参数更新，需要迭代次数多
（3）MBGD：每次使用batch个数据进行目标参数更新

6. 参考

1. 梯度下降法的三种形式BGD、SGD以及MBGD
2. 实现demo可以参考本人Git网址