0/1背包问题之动态规划法求最优解和最优解路径

一、问题介绍

给定 n 种物品和一个容量为 C 的背包，物品 i 的重量是 w_i，其价值为 v_i。问：应该如何选择装入背包的物品，使得装入背包中的物品的总价值最大？

二、问题分析

面对每个物品，我们只有选择拿(1)取或者不拿(0)两种选择，不能选择装入某物品的一部分，也不能装入同一物品多次。
把物品随机排成一排，标记为1、 2、 3……，从1号物品开始依次判断是否装包，面对当前物品有两种情况：

• 该物品的重量大于背包的容量，装不下，只能选择不装
• 该物品的重量小于背包的容量，可以装下，但是否要装，需要进一步判断，因为可能存在这样一种情况：要装该物品，就必须拿出之前装的一个物品，而这时可能会出现如下不同情况：
  2.1 【拿掉之前的一个物品并装进当前物品后 背包的总价值】<【不拿掉之前的物品且不装当前物品 背包的总价值】 ;
  2.2 【拿掉之前的一个物品并装进当前物品后 背包的总价值】>【不拿掉之前的物品且不装当前物品 背包的总价值】
  举例说明：有2个物品，重量数组w={7,6}，价值数组v={3,9}，背包容量为8。1号物品重量7小于背包容量8，放进背包，此时背包价值为3，到2号物品时，2号物品重量3也小于背包容量8，但是如果要把2号物品放进背包，就要把1号物品从背包中拿出，此时就要比较两种情况下背包的价值哪个更大，max（2号物品不放进背包，2号物品放进背包（隐含着要把1号物品取出背包））=max（3,9）=9，因此选择拿出1号物品，放进2号物品。
  当然背包容量也有可能不用取出之前的物品可以直接放下当前物品，此时肯定是放要比不放价值更大。
  因此，当物品重量小于背包总容量，也就是背包可以装下该物品时，要判断装之前和装之后背包的总价值来决定是否要装该物品。

因此，通过判断当前物品是否装包而计算当前问题的最优解时，是要用到上一个子问题的最优解的（通过判断上一个物品是否装包而计算得到），也就是说，如果当前物品不装进背包，那么上一个子问题的最优解就是当前状态的最优解，如果当前物品装包后的价值大于不装的价值，那么当前问题的最优解就是当前物品装进背包后产生的价值，这个值=上一个子问题中背包容量为【背包总容量减去当前物品重量】的情况下的最优解+当前物品价值。总之，当前问题的最优解求解过程依托于上一个子问题的各个状态下的最优解，所以在求当前问题的最优解之前要先求出之前的所有情况下的最优解。也就是要先求子问题的最优解。这里就需要用到动态规划的方法。

三、动态规划(DP)

动态规划（Dynamic Programming,DP) 与分治法的区别在于划分的子问题是有重叠的，解过程中对于重叠的部分只要求解一次，记录下结果，减少了重复计算过程。
另外，DP在求解一个问题最优解时，不是固定的计算合并某些子问题的解，而是根据各子问题的解的情况选择其中最优的。
动态规划求解具有以下性质：
最优子结构性质：最优解包含了其子问题的最优解，不是合并所有子问题的解，而是找最优的一条解线路，选择部分子最优解来达到最终的最优解。
子问题重叠性质：先计算子问题的解，再由子问题的解去构造问题的解（由于子问题存在重叠，把子问题解记录下来为下一步使用，这样就可以从备忘录中读取）。其中备忘录先记录初始状态。

四、求解过程

定义一个二维数组m[n][C]，每个元素代表一个状态，m[i][j]表示前 i 个物品放入容量为 j 的背包所能获得的最大价值，我们可以很容易分析得出m[i][j]的计算方法：

1. 初始状态
   初始状态都为0，表示前0个物品无论放入多大的背包价值都为0，容量为0的背包无论多大价值的物品都无法装进去；
2. 转移函数

if(w(i)>j)
		m[i][j]=m[i-1][j];
else
		m[i][j]=max(m[i-1][j],m[i-1][j-w(i)]+v(i));

最后一行代码就是根据“为了容量为C的背包中物品总价值最大化，第i件物品应该放入背包中吗”转化来的。v(i)表示第i件物品的价值，w(i)表示第i件物品的重量。m[i-1][j]表示不将这件物品放进背包的背包的总价值，m[i-1][j-v(i)]+w(i)表示将第i件物品放进背包后背包的总价值，比较两者，取最大值作为最终的选择。
假设有6个物品：
价值数组v = {8, 10, 6, 3, 7, 2}，
重量数组w = {4, 6, 2, 2, 5, 1}，
求背包容量C = 12时对应的m[i][j]数组。

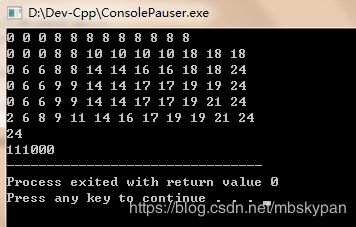
i\j	0	1	2	3	4	5	6	7	8	9	10	11	12
0	0	0	0	0	0	0	0	0	0	0	0	0	0
1	0	0	0	0	8	8	8	8	8	8	8	8	8
2	0	0	0	0	8	8	10	10	10	10	18	18	18
3	0	0	6	6	8	8	14	14	16	16	18	18	24
4	0	0	6	6	9	9	14	14	17	17	19	19	24
5	0	0	6	6	9	9	14	14	17	17	19	21	24
6	0	2	6	8	9	11	14	16	17	19	19	21	24

4.1 求解最优值的代码

#include 
#include 
using namespace std;

const int N=15;
 
int main()
{
	int v[N]={0,8, 10, 6, 3, 7, 2};
    int w[N]={0,4, 6, 2, 2, 5, 1}; 
 	int m[N][N];
	int n=6,c=12;
	memset(m,0,sizeof(m));//使用memset()函数要引入头文件
 	for(int i=1;i<=n;i++)
 	{
		for(int j=1;j<=c;j++)
		{
 			if(j>=w[i])
 				m[i][j]=max(m[i-1][j],m[i-1][j-w[i]]+v[i]);
 			else
				m[i][j]=m[i-1][j];
		}
	 } 
	 for(int i=1;i<=n;i++)//打印状态矩阵，每一个元素都表示在当前状态下（前i个物品装容量为j的背包）的最优解
	{
		 for(int j=1;j<=c;j++)
		{
			 cout<

到这一步，已经求出可以获得的最大总价值，但是不知道是装进了哪几件物品而获得的，故要根据最优解回溯找出解的组成，根据填表的原理可以有如下寻解方式：
另起一个数组x[],x[i]=0表该物体不装进背包，x[i]=1表示该物体装进背包。

1) 如果m[i][j]=m[i-1][j]，

说明有没有第i件物品都一样，因此第i件物品没有装进背包，所以x[i]=0，回到m[i-1][j]；

2) m[i][j]=m[i-1][j-w[i]]+v[i]时，

说明装了第i个商品，该商品是最优解组成的一部分，x[i]=1,随后我们得回到装该商品之前，即回到m[i-1][j-w(i)]；

3) 一直遍历到i＝0结束为止，所有解的组成都会找到。

4.2 求最优解路径的代码（递归法）

void FindWhat(int i,int j)//寻找解的组成方式
{
    if(i>=0)
    {
        if(m[i][j]==m[i-1][j])//相等说明没装
        {
            item[i]=0;//全局变量，标记未被选中
            FindWhat(i-1,j);
        }
        else if( j-w[i]>=0 && m[i][j]==m[i-1][j-w[i]]+v[i] )
        {
            item[i]=1;//标记已被选中
            FindWhat(i-1,j-w[i]);//回到装包之前的位置
        }
    }
}

4.3 求最优解路径的代码（非递归法）

 void traceback()
{
    for(int i=n;i>1;i--) //从状态矩阵右下角的最优值开始往前回溯
    {
        if(m[i][c]==m[i-1][c])//如果当前状态的解等于上一个状态的解，表示当前物品没有放进背包
            x[i]=0;
        else//如果当前状态的解不等于上一个状态的解，说明当前物品被放进背包
        {
            x[i]=1;
            c-=w[i];//当前状态的最优解是通过m[i-1][c-w[i]]+v(i)得到的，
         			   //因此下一步从m[i-1][c-w[i]]开始继续回溯，
         			   	//按照同样的方法判断第i-1个物品有没有被装进背包
        }
    }
    x[1]=(m[1][c]>0)?1:0; //上面的for循环可以判断第2,3,4……个物品是否被装进背包
    									//因此还需要单独对第一个物品进行判断
    									//如果经过上面的for循环之后背包剩余容量c能够装下第一个物品
    									//也就是m[1][c]>0，说明第一个物品肯定被装进了背包
}

4.4 结合前两段的完整代码

#include 
#include 
using namespace std;

const int N=15;

int v[N]={0,8, 10, 6, 3, 7, 2};
int w[N]={0,4, 6, 2, 2, 5, 1}; 
int m[N][N];
int x[N];
int n=6,c=12;

void FindWhat(int i,int j)//递归法寻找解的组成方式
{
    if(i>=0)
    {
        if(m[i][j]==m[i-1][j])//相等说明没装
        {
            x[i]=0;//全局变量，标记未被选中
            FindWhat(i-1,j);
        }
        else if( j-w[i]>=0 && m[i][j]==m[i-1][j-w[i]]+v[i] )
        {
            x[i]=1;//标记已被选中
            FindWhat(i-1,j-w[i]);//回到装包之前的位置
        }
    }
}

/* void traceback()//非递归法寻找解的组成方式
{
    for(int i=n;i>1;i--)
    {
        if(m[i][c]==m[i-1][c])
            x[i]=0;
        else
        {
            x[i]=1;
            c-=w[i];
        }
    }
    x[1]=(m[1][c]>0)?1:0;
}
*/
 
int main()
{

	memset(m,0,sizeof(m));
 	for(int i=1;i<=n;i++)
 	{
		for(int j=1;j<=c;j++)
		{
 			if(j>=w[i])
 				m[i][j]=max(m[i-1][j],m[i-1][j-w[i]]+v[i]);
 			else
				m[i][j]=m[i-1][j];
		}
	 }
 
/*	 for(int i=1;i<=n;i++)//打印状态矩阵
	{
		 for(int j=1;j<=c;j++)
		{
			 cout<

输出：111000，代表前三个物品装进了背包，后三个没有装进背包。