【Graph Embedding/Network Embedding 图嵌入/网络表示学习】主要工作(Deepwalk/LINE/node2vec)总结
前言
首先,花了两年时间从Web开发往AI转行,也阔别CSDN已久。这是回归后第一篇笔记,最开始先放一张非常全面的图,来自清华大学唐杰老师的演讲PPT,很全面地总结了近几十年来人工智能/深度学习算法发展进程中的主要工作和大佬们:从上往下的四个区域分别代表着卷积神经网络CNN、自动编码器AutoEncoder、循环神经网络RNN、强化学习Reinforcement Learning。

而没有提到的图神经网络(Graph Neural Network, GNN),算是目前比较新且逐渐热门的方向,它以CNN的延伸泛化(GCN)为模型基础、以语言模型(word2vec)衍生出来的图嵌入/表示学习方法为数据基础,解决图结构中的分类、预测、可视化等问题。
这篇主要总结图嵌入/表示学习方法,侧重于思路和算法,不涉及具体代码实现。
基础
概念
图嵌入(Graph Embedding)/图表示学习(Graph Representation Learning),也称作网络嵌入(Network Embedding)/网络表示学习(Network Representation Learning),本质上就是给定一个图(网络),学习其中每一个节点Vertice甚至边Edge在低维空间上的表示,即稠密、实值的低维向量。
word2vec
简单介绍一下word2vec:它是2013年被发明出来的工具,已经成为自然语言处理领域的基础,它的主要作用是把词内容表示成向量,即Word Embedding,向量可以表达不同词之间的相似度和类比关系,用来作为后续具体机器学习任务的模型的输入。
word2vec是基于语言模型(language model)的一种“副产物”:语言模型尝试在词语x和上下文y之间建立映射f,在模型训练后,神经网络中被x的one-hot encoder模式激活的部分权重参数W组成一个向量vx,这个vx就是词x的唯一表示,也就是x的词向量。
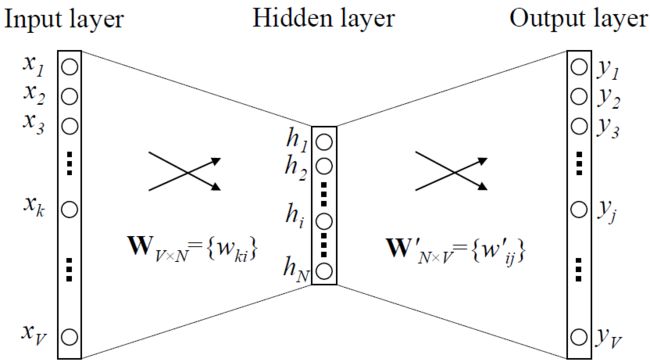
上文说到的语言模型,主要有两类:
- Skip-gram模型:用一个词作为输入,预测它的上下文。(1-n)
- 词袋(continuous bag of words, CBOW)模型:用一个词的上下文作为输入,来预测这个词本身。(n-1)
此外,在训练语言模型时,由于实际工作中文本的词语个数会非常多,导致计算困难,所以需要使用*分层softmax(Hierarchical Softmax)和负采样(negative sampling)*这两种技巧来加速训练过程。
这一块的内容是DeepWalk的基础,没有深入细节,知道原理即可。总而言之,word2vec利用词与词的共现关系,通过两类语言模型Skip-gram和CBOW实现了文本中词的向量表示。
DeepWalk
生活中有许多天然形成的图(Graph)结构,比如社交网络、交通路网、化学元素,也有人为制造的图结构比如知识图谱,这些图不同于NLP中的文本和语音识别中的声波序列,也不同于CV中规则方网状结构的图片。
思路
关于一张图G的定义如下,其中V是顶点vertice的集合,E是边edge的集合。
G = ( V , E ) G=(V, E) G=(V,E)在word2vec中,文本或者句子可以理解为由词组成的序列,所以该方法也可以理解为对于序列中节点特征的嵌入/表示学习。但是,当我们的对象是图时,因为数据结构的根本区别,加上图的稀疏性,word2vec就失效了。
那么如何在图上做嵌入/表示学习呢?作者认为既然已经有成熟的word2vec了,大可将其利用起来而不需要另起炉灶。所以问题就转化为:如何将图转换为序列以供word2vec使用?解决方案是:随机游走(random walk)。
算法
随机游走是一种可重复访问已访问节点的深度优先遍历算法。
DeepWalk核心算法如下图所示。首先初始化顶点的表示矩阵 Φ \varPhi Φ,用V构建二叉树T用于分层softmax。算法中的核心是3-9行,外层循环指定了游走次数 γ \gamma γ,即每个节点会产生多少个游走序列。内层循环遍历了图中每一个节点 v i v_i vi:给定当前访问起始节点,不断从当前节点的邻居中随机选择一个访问,直到访问序列长度达到t,生成当前节点的游走序列 W v i W_{v_i} Wvi,然后用SkipGram(前文中的Skip-gram)更新其向量表示 Φ \varPhi Φ( ω \omega ω是语言模型中的窗口大小)。

SkipGram算法如下图所示。外层循环是序列中的每个词,内层循环是其窗口大小为 ω \omega ω的词序列,运用似然函数J对当前词的表示向量 Φ \varPhi Φ进行学习率为 α \alpha α梯度下降更新。
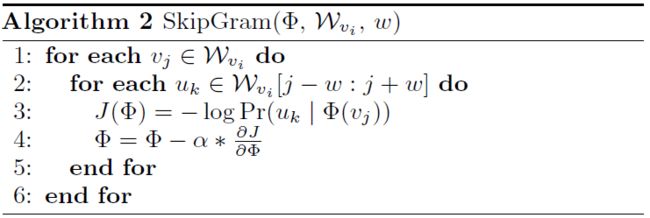
流程概览
以上介绍了DeepWalk的算法,下面从流程角度再过一遍。
如下图所示,由节点 v 4 v_4 v4开始的随机游走序列为 v 4 v_4 v4- v 3 v_3 v3- v 1 v_1 v1- v 5 v_5 v5- v 1 v_1 v1…将其中的中间节点 v 1 v_1 v1映射到初始的表示向量 Φ ( v 4 ) \varPhi(v_4) Φ(v4)。分层softmax将序列转为二叉树以降低复杂度加速训练,然后计算 P r ( v 3 ∣ Φ ( v 1 ) ) Pr(v_3|\varPhi(v_1)) Pr(v3∣Φ(v1))和 P r ( v 5 ∣ Φ ( v 1 ) ) Pr(v_5|\varPhi(v_1)) Pr(v5∣Φ(v1)),即序列路径从根 v 1 v_1 v1开始到 v 3 v_3 v3和 v 5 v_5 v5结束的概率分布,从而使得节点 v 1 v_1 v1的表示向量 Φ ( v 1 ) \varPhi(v_1) Φ(v1)向着最大化其上下文为 v 3 v_3 v3和 v 5 v_5 v5的方向更新。
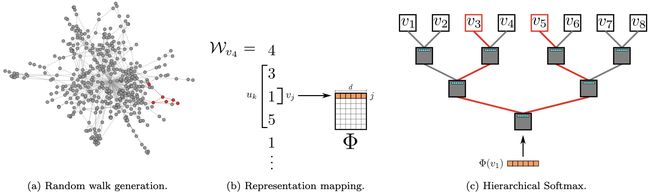
其他两点补充说明:
- 随机游走可以获得图中节点的局部上下文信息,越近的节点游走到的概率越大,因此在图上相似节点的表示也会相似。
- 随机游走是局部的,可以同时在图的不同节点同时游走,并行化以减少采样时间。同时也可以适应图的局部变化,不需要 每一次变化都重新计算整个网络的游走。
总结
DeepWalk是该领域非常经典的工作,可以说开辟了新纪元。它巧妙地通过随机游走将图/网络转换为序列,再使用word2vec进行表示学习。后续若干重要工作都是在DeepWalk的基础上展开的。
LINE
DeepWalk的工作逐渐引起关注,也逐渐暴露出了它的一些不足:
- 并没有提供明确的目标来阐明保留哪些图/网络属性。
- 仅适用于未加权的图/网络。
思路
为了弥补上述DeepWalk的不足,LINE被提出来,主要是建立了一套新的体系来定义节点间的关系。
如下图所示,其中边可以是无向/有向的、加权/未加权的。顶点6和7应该被紧密地放置在低维向量空间中,因为它们通过一个强连接连接在一起。顶点5和6也应该被紧密放置,因为它们有相似的邻居。

所以LINE
-
将节点6和7的关系定义为一阶相似度(first-order proximity):
若 u , v u, v u,v之间存在直连边,则边权 ω u v \omega_{uv} ωuv为两个节点的相似度,若不存在直连边则一阶相似度为0。在上图中,6和7之间存在直连边且边权大,则两者一阶相似度高且认为它们相似;而5和6之间不存在直连边,则两者一阶相似度为0。 -
将节点5和6的关系定义为二阶相似度(second-order proximity):
若 p u = ( w u 1 , w u 2 , . . . , w u ∣ V ∣ ) p_u=(w_{u1},w_{u2},...,w_{u|V|}) pu=(wu1,wu2,...,wu∣V∣)表示节点 u u u与所有其他节点间的一阶相似度,则 u u u和 v v v的二阶相似度可以通过 p u p_u pu和 p v p_v pv的相似度表示。若 u u u和 v v v之间不存在相同的邻居节点,则二阶相似度为0。在上图中,5和6之间不存在直连边,但有共同的邻居节点{1, 2, 3, 4},则两者二阶相似度高且认为它们相似。
算法
一阶相似度
- 对于每个无向边 ( i , j ) (i,j) (i,j),定义节点 v i v_i vi和 v j v_j vj的联合概率分布为 p 1 ( v i , v j ) = 1 1 + exp ( − u i → T ⋅ u j → ) p_1(v_i,v_j)=\frac{1}{1+\exp(-\overrightarrow{u_i}^T\cdot\overrightarrow{u_j})} p1(vi,vj)=1+exp(−uiT⋅uj)1
u i → \overrightarrow{u_i} ui是节点 v i v_i vi的低维向量表示。 - 定义经验分布为 p 1 ^ = w i j W , W = ∑ ( i , j ) ∈ E w i j \hat{p_1}=\frac{w_{ij}}{W},W=\displaystyle\sum_{(i,j)\in{E}}w_{ij} p1^=Wwij,W=(i,j)∈E∑wij
- 优化目标为最小化 O 1 = d ( p 1 ^ ( ⋅ , ⋅ ) , p 1 ( ⋅ , ⋅ ) ) O_1=d(\hat{p_1}(\cdot,\cdot),p_1(\cdot,\cdot)) O1=d(p1^(⋅,⋅),p1(⋅,⋅))
其中 d ( ⋅ , ⋅ ) d(\cdot,\cdot) d(⋅,⋅)是两个分布的距离。 - 采用KL散度衡量当前与经验概率分布差异,并忽略常数项后目标函数为 O 1 = − ∑ ( i , j ) ∈ E w i j log p 1 ( v i , v j ) O_1=-\displaystyle\sum_{(i,j)\in{E}}w_{ij}\log{p_1(v_i,v_j)} O1=−(i,j)∈E∑wijlogp1(vi,vj)
一阶相似度仅适用于无向图。
二阶相似度
对于每个节点维护两个表示向量,一个是该节点本身的向量,一个是该节点作为其他节点上下文的向量。
- 对于有向边 ( i , j ) (i,j) (i,j),定义给定节点 v i v_i vi条件下,产生上下文节点 v j v_j vj的概率为 p 2 ( v j ∣ v i ) = exp ( u j → T ⋅ u i → ) ∑ k = 1 ∣ V ∣ exp ( u k → T ⋅ u i → ) p_2(v_j|v_i)=\frac{\exp(\overrightarrow{u_j}^T\cdot\overrightarrow{u_i})}{\displaystyle\sum_{k=1}^{|V|}\exp(\overrightarrow{u_k}^T\cdot\overrightarrow{u_i})} p2(vj∣vi)=k=1∑∣V∣exp(ukT⋅ui)exp(ujT⋅ui)其中|V|为上下文节点的个数。
- 定义经验分布为 p 2 ^ ( v j ∣ v i ) = w i j d i , d i = ∑ k ∈ N ( i ) w i k \hat{p_2}(v_j|v_i)=\frac{w_{ij}}{d_i},d_i=\displaystyle\sum_{k\in{N(i)}}w_{ik} p2^(vj∣vi)=diwij,di=k∈N(i)∑wik其中 w i j w_{ij} wij是边 ( i , j ) (i,j) (i,j)的边权, d i d_i di是节点 v i v_i vi的出度。
- 优化目标为最小化 O 2 = ∑ i ∈ V λ i d ( p 2 ^ ( ⋅ ∣ v i ) , p 2 ( ⋅ ∣ v i ) ) O_2=\sum_{i\in{V}}\lambda_id(\hat{p_2}(\cdot|v_i),p_2(\cdot|v_i)) O2=i∈V∑λid(p2^(⋅∣vi),p2(⋅∣vi))其中 λ i \lambda_i λi为控制节点重要性的因子,可以通过节点的度数或者PageRank等方法估计得到。
- 采用KL散度衡量当前与经验概率分布差异,并设 λ i = d i \lambda_i=d_i λi=di且忽略常数项后目标函数为 O 2 = − ∑ ( i , j ) ∈ E w i j log p 2 ( v i ∣ v j ) O_2=-\displaystyle\sum_{(i,j)\in{E}}w_{ij}\log{p_2(v_i|v_j)} O2=−(i,j)∈E∑wijlogp2(vi∣vj)
优化
本工作中运用到了两种优化方法,负采样(Negative Sampling)和边采样(Edge Sampling)。负采样提高了二阶相似度遍历所有节点的计算速度,在此不做详细介绍。
我们的目标函数在log之前还有一个权重系数 w i j w_{ij} wij,在使用梯度下降方法优化参数时, w i j w_{ij} wij会直接乘在梯度上。如果图中的边权方差很大,则很难选择一个合适的学习率。若使用较大的学习率那么对于较大的边权可能会引起梯度爆炸,较小的学习率对于较小的边权则会导致梯度消失。
对于上述问题采用边采样:从原始的带权边中进行采样,每条边被采样的概率正比于原始图中边的权重,这样把 w i j w_{ij} wij从优化转移到了采样的过程中,既解决了学习率的问题,又没有带来过多的存储开销。
总结
- LINE可以轻松扩展到具有数百万个节点和数十亿条边的图/网络。 它精心设计了目标函数,这些目标函数保留了一阶和二阶邻近度,并可用于加权图和有向图(二阶)。
- LINE在实际训练时,分别训练保留一阶近似和二阶近似的模型,然后将这两种方法训练的每个节点的嵌入连接起来。
- LINE提出了一种边采样的优化方法,解决了加权边随机梯度下降的局限性,且不影响效率。
node2vec
如果说DeepWalk倾向于深度优先遍历DFS,那么LINE就倾向于广度优先遍历BFS,那么是否有一种方法,可以将两者结合起来呢?
思路
在下图中,我们观察到 u u u和 s 1 s_1 s1、 s 2 s_2 s2、 s 3 s_3 s3、 s 4 s_4 s4属于同社区紧密相连的节点,而 u u u和 s 6 s_6 s6是两个不同区域中的节点,有相同的结构角色(都是区域中心点)。 因此,必须有一个灵活的算法来同时学习以下两个原则的节点表示形式:
- 结构等价性(structural equivalence):具有相似的结构角色的节点具有相似的嵌入。
为了使向量表示的结果能够表达图/网络的结构等价,需要让随机游走的过程更倾向于广度优先搜索(BFS),因为BFS更喜欢游走到跟当前节点有直接连接的节点上,因为基于角色的结构等价性可以通过观察每个节点的直接邻域来推断,所以产生了与结构等价性密切对应的嵌入。(看的更近而全反而能明白结构等价) - 同质性(homophily):将来自同一图/网络区域的节点紧密地嵌入在一起。
为了使向量表示的结果能够表达图/网络的结构性,需要让随机游走的过程更倾向于深度优先搜索(DFS),因为DFS会更倾向于游走探索到更大的网络和更远的节点上。抽样节点更准确地反映了邻居的宏观情况,这在基于同质性的区域推断中是必不可少的。(看的更远而泛反而能明白同质)
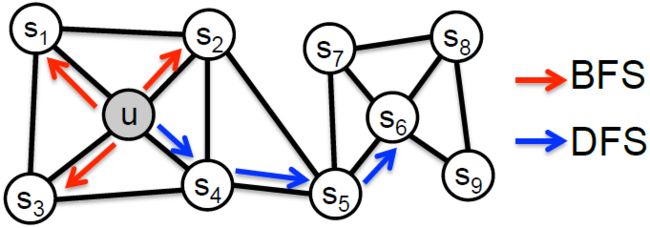
算法
为了实现上述两个原则的表示方式,node2vec在算法中通过调整节点间的跳转概率来调整在BFS和DFS间的倾向性。
如下图所示,当从节点 t t t跳转到节点 v v v后,下一步从节点 v v v出发该如何跳转?

设定从节点 v v v跳转到下一个节点 x x x的概率为
π v x = α p q ( t , x ) ⋅ ω v x \pi_{vx}=\alpha_{pq}(t,x)\cdot\omega_{vx} πvx=αpq(t,x)⋅ωvx
其中 ω v x \omega_{vx} ωvx是边 v x vx vx的权重, α p q ( t , x ) \alpha_{pq}(t,x) αpq(t,x)的定义如下:
α p q ( t , x ) = { 1 p if d t x = 0 1 if d t x = 1 1 q if d t x = 2 \alpha_{pq}(t,x)=\begin{cases}\frac{1}{p}&\text{if }d_{tx}=0\\1 &\text{if }d_{tx}=1\\\frac{1}{q} &\text{if }d_{tx}=2\end{cases} αpq(t,x)=⎩⎪⎨⎪⎧p11q1if dtx=0if dtx=1if dtx=2
其中, d t x d_{tx} dtx指的是节点 t t t到节点 x x x的距离,参数 p p p和 q q q共同控制着随机游走的倾向性。
1 参数 p p p被称为返回参数(return parameter), p p p越小,随机游走回节点 t t t的可能性越大,node2vec就更注重表达网络的结构等价性,即广度优先搜索BFS。
2 参数 q q q被称为进出参数(in-out parameter), q q q越小,则随机游走到远方节点的可能性越大,node2vec更注重表达网络的同质性,即深度优先搜索DFS。
总结
相比于LINE侧重于制定规则,node2vec其实才是DeepWalk最直接的改进版。它通过调整随机游走权重的方法,使图嵌入/表示学习的结果在图/网络的结构等价性和同质性中进行权衡。
结语
本文介绍了图嵌入/网络表示学习领域比较重要的三个工作,重点在于它们的思路、算法以及其中关联。
- DeepWalk建议使用统一的随机游走进行搜索。 这种策略的明显局限性在于,它使我们无法控制所探索的区域,以及只适用于未加权图/网络。
- LINE主要提出了广度优先策略,对节点进行采样并仅在一阶和二阶邻居上独立优化似然性。 这种探索的效果更容易表征,但是它难以表示高阶邻居,在进一步探索节点时没有灵活性。
- node2vec的搜索策略通过参数p和q探索网络邻域,在广度优先搜索和深度优先搜索之间进行权衡。
后来也有研究者通过数学分析,将以上网络表示学习等价为矩阵分解,即奇异值分解(SVD)。可以简单(但不严谨)地理解为将完整的图嵌入(矩阵)分解成了具体的节点嵌入(向量)*边权(矩阵),这个矩阵分解的理论也为后来的GNN打下了基础。
参考文献:
[1]B. Perozzi, R. Al-Rfou, and S. Skiena, “DeepWalk: online learning of social representations,” in Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining - KDD ’14, New York, New York, USA, 2014, pp. 701–710, doi: 10.1145/2623330.2623732.
[2]J. Tang, M. Qu, M. Wang, M. Zhang, J. Yan, and Q. Mei, “LINE: Large-scale Information Network Embedding,” in Proceedings of the 24th International Conference on World Wide Web - WWW ’15, Florence, Italy, 2015, pp. 1067–1077, doi: 10.1145/2736277.2741093.
[3]A. Grover and J. Leskovec, “node2vec: Scalable Feature Learning for Networks,” in Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining - KDD ’16, San Francisco, California, USA, 2016, pp. 855–864, doi: 10.1145/2939672.2939754.
【Graph Embedding】DeepWalk:算法原理,实现和应用
【Graph Embedding】LINE:算法原理,实现和应用
[NLP] 秒懂词向量Word2vec的本质
深度学习中不得不学的Graph Embedding方法转载 | 认知推理:从图表示学习和图神经网络的最新理论看AI的未来