机器学习笔记笔记（乏味的猫）——概述

讲在课前的话（18分钟就讲了后面这些课程要讲什么内容。。。balabala话有点多）

机器学习内容：
机器学习概述
回归算法
-线性回归
-多项式回归
-lasso回归
-ridge回归
-逻辑回归
KNN
决策树
集成算法
SVM
-线性可分svm
-和函数的svm
KMeans聚类算法
多标签的算法
贝叶斯算法
EM算法
HMM模型
主题模型
特征工程

数学知识回顾

建议大家把numpy，pandas，matplotlib官网文档，api过一遍

导数（简单求导公式，复合函数求导，链式法则求导）
导数和梯度的含义和作用
taylor公式（用多项式来拟合函数）
联合概率，条件概率，全概率公式，贝叶斯公式
期望，方差，协方差（了解它们表示数据具有什么样的特性）
大数定理，中心极限定理
最大似然估计
向量，矩阵的运算
向量，矩阵的求导
SVD，QR分解

常见函数（实际上就是高中数学讲的那些函数，以及运算法则）
机器学习领域，凸函数开口向上

常见导函数

偏导数：多变量函数中，保持其他变量不变关于其中一个变量的导数。

梯度：梯度是一个向量，表示某一函数再该点处的方向导数沿着该方向取得的最大值，变化率最大（即该梯度向量的模）
$$\nabla (x_1,x_2)=(\frac{\partial f(x_1,x_2)}{\partial x_1},\frac{\partial f(x_1,x_2)}{\partial x_2})$$

泰勒公式：用一个函数再某一点的信息描述其附近取值的公式。
如果函数足够平滑，再已知函数某一点各阶导数值的情况下，泰勒公式可以利用这些导数值来做系数构建一个多项式近似函数在这一点的邻域中的值。

最大似然估计：一种参数估计方法
步骤：
写出似然函数
对似然函数取对数
求导数
解似然方程

QR分解：将矩阵分解为一个正交矩阵与上三角矩阵的乘积
Q为正交矩阵，R为上三角矩阵
实际中QR分解经常被用来解决线性最小二乘问题

SVD（奇异值分解）：
一种重要的矩阵分解方法，可以看作是对称方阵再任意矩阵上的推广

向量的导数

向量偏导公式
$$\frac{\partial Ax}{\partial x}=A^T$$

$$\frac{\partial Ax}{\partial x^T}=A$$

$$\frac{\partial x^{T}A}{\partial x}=A$$

标量对向量的导数
$$\frac{\partial (x^{T}Ax)}{\partial x}=(A^T+A)\cdot x$$

若A为对称矩阵，则有
$$\frac{\partial (x^{T}Ax)}{\partial x}=2Ax$$

Python科学计算库回顾
numpy数学计算基础库：N维数组，线性代数计算，傅里叶变换，随机数等
Scipy数值计算库：线性代数，拟合与优化，插值，数值积分，稀疏矩阵，图像处理，统计等
Pandas数据分析库：数据导入，整理，处理，分析
Matplotlib绘图库：绘制二维图形和图表
https://scipy.org/

基本的爬虫用法要会

机器学习：模拟人认知的一个过程，从数据中获得一个假设的函数g，使其非常接近目标函数f的效果

机器学习理性认识：
输入
输出
目标函数
输入数据D
最终公式

机器学习无法找到一个完美的f

基本概念：
算法
模型
评估

向量/特征向量
矩阵/特征矩阵
标量/目标属性

拟合：构建的算法模型符合给定数据的特征
$x_i$:x向量的第i维度的值
$x^{(i)}$:第i个样本的x向量
鲁棒性：健壮性，当存在异常数据的时候，算法也会拟合数据
过拟合：算法太符合样本数据的特征，对于实际生产中的数据无法拟合
欠拟合：算法不太拟合样本的数据特征

机器学习常见应用框架：
scikit-learn
Mahout
Spark MLlib

关于sklearn的安装
pip也行，anaconda里面安装也行

sklearn algorithm cheat sheet

商业场景：
个性化推荐
精准营销
客户细分
预测建模及分析

模式识别
计算机视觉
语音识别
数据挖掘
统计学习
自然语言处理

机器学习算法类别讲解：

conda info scikit-kearn可以看版本信息

机器学习分类：
有监督
无监督
半监督

有监督：
判别式模型（logistic回归，决策树，svm，knn，神经网络）
生成式模型（HMM,朴素贝叶斯，GMM，LDA）

生成式模型更普适，判别式模型更直接，目标性更强

生成式模型关注数据是如何产生的，找的是数据分布模型；而判别式模型找的是差异性，找的是分类面。

生成式模型可以产生判别式模型

无监督学习：
试图学习或者提取数据别后的数据特征，常见的算法有聚类，降维，文本处理（特征抽取）等
一般作为有监督学习的前期数据处理
功能：从原始数据中抽取出必要的表情信息

半监督学习：主要考虑如何利用少量样本和大量的未标注样本进行训练和分类的问题。

依赖于模型假设，主要三大类：
平滑假设
聚类假设
流行假设

算法分四大类：
版监督分类，半监督回归，半监督聚类，半监督降维

缺点：抗干扰能力弱

另一种分类：
分类
聚类
回归
关联规则：获取隐藏在数据项之间的关联或相互关系

TOP10
C4.5分类决策树 算法，ID3的改进算法
C5.0 商业版本 收钱
CART 分类与回归树可以分类，可以回归
knn
NaiveBayes 贝叶斯分类模型，适合属性相关性较小的时候；如果属性相关性大决策树模型更好
svm 一种有监督学习的统计学习方法
EM 最大期望算法（和MLE同根同祖）
apriori 关联规则挖掘算法
K-Means 聚类算法，功能：讲n个对象根据属性特征分为k个分割 属于无监督学习
PageRank google重要搜索算法之一
AdaBoost 迭代算法，利用多个分类器进行数据分类

机器学习开发流程：
数据收集
数据预处理
特征提取
模型构建
模型测试评估
投入使用（模型部署与整合）
迭代优化

数据收集和存储

数据来源：
用户行为数据
业务数据
外部第三方数据

数据存储：
需要存储的数据：原始数据，预处理后的数据，模型结果
存储设施：磁盘，mysql，HDFS，HBase，Solr，Elasticsearch，Kafka，Redis等

数据收集方式：
Flume & Kafka

机器学习常用数据集

数据清洗和转换
实际生产中比较耗时的部分

预处理的操作主要包括以下几个部分：
数据过滤
处理数据缺失
处理可能的异常，错误或者异常值
合并多个数据源数据
数据汇总

数据适合机器学习模型的表示形式：

• 将类别数据编码为对应的数值表示（一般使用1-of-k\哑编码方法）
• 从文本中提取有用数据（一般使用词袋法或TF-IDF）
• 处理图像或者音频数据（像素，声波，音频，振幅等<傅里叶变换>）
• 对特征进行正则化，标准化，以保证同一模型不同输入变量的取值范围相同
• 数值数据转换为类别数据以减少变量的值，如年龄分段
• 对数值数据进行转换，比如对数转换
• 对现有变量进行组合郭转换以生成新特征

1-of-k(哑编码)
功能：将非数值型的特征值转换为数值型的数据
描述：假设变量的取值有k个，如果对这些值用1到k编序，可用维度为k的向量来表示一个变量的值。在这样的向量里，该取值所对应的序号所在的元素为1，其它元素均为0

文本数据抽取

• 词袋法：将文本作为一个无序的数据集合，文本特征可以采用文本中的词条T进行提现，那么文本中出现的所有词条及其出现的次数就可以提现文档的特征
• TF-IDF:词条的重要性随着它在文件中出现的次数成正比增加，但同时会随着它在语料库中出点的品略成反比下降；也就是说词条在当前文本中出现的次数越多，表示改词条对当前文本的重要性越高，词条在所有文本（语料库）中出现的次数越少，说明这个词条对文本的重要性越高。
  TF（词频）：某个词条在文本中出现的次数，一般会对其进行归一化处理
  IDF（逆向文件频率）：一个词条的重要性度量，一般计算方式问语料库中总文件数目除以包含该词语的文件数目，在讲得到的商取对数得到。
  TF-IDF实际上是TF*IDF

特征属性：
数值型
含义：体现样本的特性

模型训练及测试：对特定任务最优建模方法的选择或者对特定模型最佳参数的选择

交叉验证：在训练集上运行模型并在测试集中测试效果，迭代进行数据模型的修改

模型的选择会尽可能多以比较执行结果

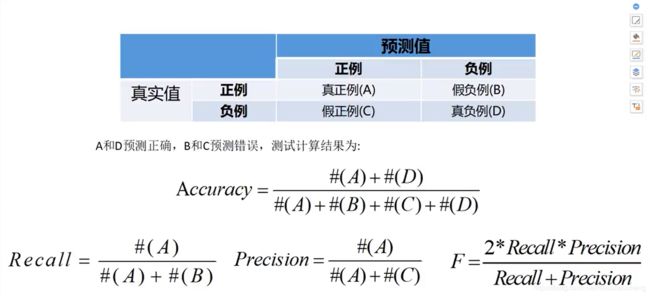
模型的测试：
$$准确率=\frac{提取出的正确样本数}{总样本数}$$
$$召回率=\frac{正确的正例样本数}{样本中的正例的样本数}$$
$$精准率=\frac{正确的正例样本数}{预测为正例的样本数}$$
$$F值=\frac{精准率\ast 召回率\ast 2}{精准率+召回率}$$
F值为正确率和召回率的调和平均值

混淆矩阵

ROC
描述的是分类混淆矩阵中FPR-TPR两个量的相对变化情况
纵轴：真正例率
横轴：假正例率
反应而正之间的权衡情况

Arae Under Curve ROC曲线下的面积 面积不会大于1
AUC值越大表达模型越好
AUC=1 完美的分类器
0.5 AUC=0.5 没预测价值，和随机猜一样
AUC<0.5 比随机猜还差

分类算法评估方式

回归算法评估方式

模型部署和整合