An introduction to Policy Gradients with Cartpole and Doom（四）

https://www.freecodecamp.org/news/an-introduction-to-policy-gradients-with-cartpole-and-doom-495b5ef2207f/

前两篇文章介绍了Q-learning和DQL，都是value-based的强化学习算法。为了决定该state选择哪个action，我们通过Q-value来完成决策。因此，在value-based学习中，policy仅仅是因为action-value的预测而存在。
这篇，我们来学习policy-based的强化学习算法——Policy Gradients。
我们将应用到两个agents上。第一个是学习保持棒的平衡。

第二个是在Doom hostile中学会收集医药包来存活。

在policy-based方法中，并不是去学习一个价值函数，我们直接学习映射state到action的policy函数。
这意味着我们直接尝试优化policy函数$\pi$，并不需要去担心价值函数。
当然，我们可以使用价值函数来优化policy参数，但是价值函数不用来选择action。
该篇，我们会学习：

• Policy Gradient是什么，它的优点和缺点是什么

Why using Policy-Based methods?

Two types of policy

一个policy可以是确定的，也可以是随机的。
一个确定的policy也就是一个将state映射到actions上的policy。你给它一个state，函数返回采取的action。

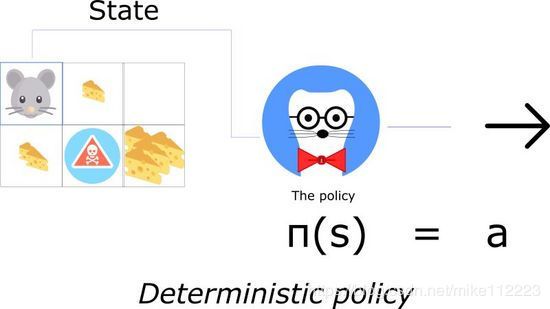
确定的policys在确定的环境中使用。在env中采取actions就决定了输出，不存在不确定性。例如，下棋时，你移动你的棋子从A2到A3，那么你可以确定你的棋子会移动到A3。
另一方面，一个随机的策略输出的是一个基于actions的概率分布。

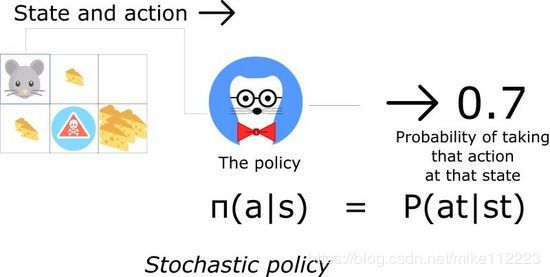
这意味着我们只有采取该action的概率。
随机policy用到env不确定的情况下。我们称这个过程Partially Observable Markov Decision Process（POMDP）。
大多数时间，我们会使用第二种policy。

Advantages

但是DQL已经很好了，为什么我们还要使用policy-based强化学习方法呢？
这里有三个使用Policy Gradients的主要优点。

Convergence

第一，policy-based方法有更好的收敛特性。
value-based方法的一个问题是在训练时，会有强烈的振荡。这是因为action的选择会因为预测的action values的任意微小的改变产生很大改变。
另一方面，policy gradient仅仅跟随梯度去寻找最优参数，我们可以在每一步上看到我们policy的平滑更新。
因为我们是跟随梯度来寻找最优参数的，这就确保我们会收敛到局部最优或者全局最优。

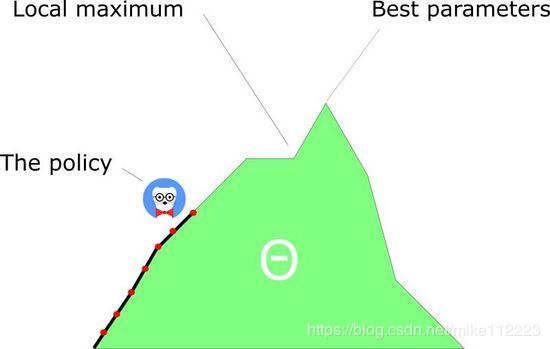
Policy gradients are more effective in high dimensional action spaces

第二个有点就是policy gradients在高维动作空间或者使用连续actions时更加有效。
DQL的问题就是它对每个可能的action都赋予了一个score。
但是如果我们有无限可能的动作呢？
比如，自动驾驶，在每个state，你有无数个动作选择（转15°，17.2°，按喇叭…）。
而policy-based方法，仅仅调整参数就行了：你开始理解最大值是什么，而不是在每一步直接预测最大值。

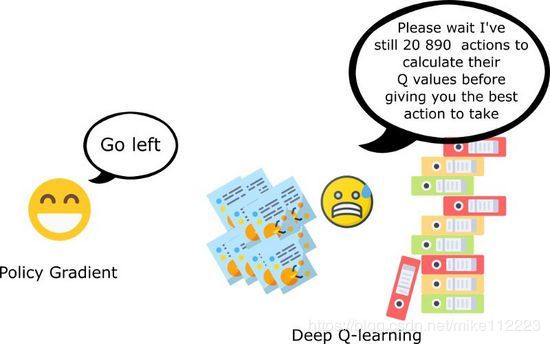
Policy gradients can learn stochastic policies

第三个优点是，policy gradient可以学习一个随机policy，但是价值函数不行。这就有两个结果。
第一，我们不需要施加一个探索/利用的权衡。一个随机policy就允许我们的agent对state空间进行探索。这是因为它输出的是一个关于actions的概率分布。结果就是不需要对探索/利用进行硬编码。
同时我们也解决了感知混淆问题。感知混淆是我们有两个看起来一样（或实际一样）的state，但是需要不同的actions。
比如，我们有一个智能真空吸尘器，它的目标是吸掉灰尘同时要避免杀死仓鼠。

我们的真空吸尘器只能理解墙在哪里。
问题是两个标红的state，它们是相似的states，因为在这两个状态agent都能感知到上面和下面的墙。
一个确定的policy，在标红的state要么左移，要么右移。显然不管哪种都会使我们的agent被困住，然后无法吸到灰尘。

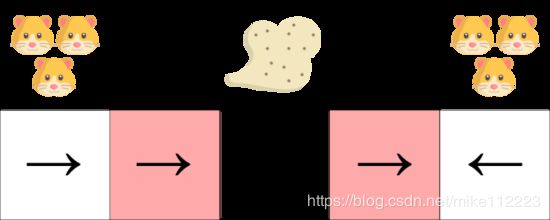
在value-based的强化算法中，我们学习一个类似确定的policy（“$ϵ$贪心策略”）。结果就是，我们的agent在找到灰尘之前会花费大量的时间。
另一方面，一个最优的随机policy是在该状态下随机左右移。结果就是，不会被困住，并且会以最高的概率达到目标state。

Disadavntages

自然地，Policy gradients有一个很大的缺点。大多数情况，它们都会收敛到一个局部最优解上，而不是全局最优。
不像DQL，总是尝试要去达到最大值，policy gradients收敛的更慢。它们会需要训练更长的时间。
但是，我们来看看解决这个问题的方案。

Policy Search

我们有policy$\pi$ 以及其参数$\theta$。$\pi$输出一个关于actions的概率分布。
$${\pi }_{\theta }(a|s)=P[a|s]$$
哇哦！但是我们怎样知道我们的policy是好是坏呢？
记住policy可以被看做是一个优化问题。我们必须找到最优参数来最大分数函数$J(\theta )$。
$$J(\theta )=E_{\pi \theta }[\sum \gamma r]$$
这里有两步：

• 用一个policy分数函数$J(\theta )$来评估policy
• 使用policy gradient上升来找到最优参数

First Step：the Policy Score function $J(\theta )$

为了评估policy效果，我们使用目标函数（或者策略分数函数）来计算policy的期望回报。
对于优化策略，有三种等效的方法。选择仅取决环境和你的目标。
第一，在情节的环境中，我们可以使用一个起始value，然后计算从第一个时间步（G1）开始得到的平均回执。这是整个情景的累计折扣回报。

这个思路是很简单的。如果我总是从state s1出发，那么我从开始到最后所能得到的总reward是多少呢？
我们想要找到一个最大化G1的策略，因为这会是最优的策略。这是基于我们在第一篇文章提到的reward假设。
例如，我们玩一个新的弹球游戏，在打掉20个砖块之后，我没有接到球（游戏结束）。这时新的情景又会从同一个state开始。

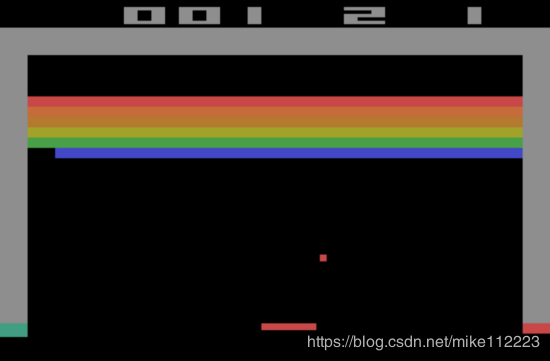
我使用$J_1(\theta )$来计算分数。击中20个砖块很不错，但是我想要提升我的分数。为此，我需要通过调整参数来提升actions的概率分布。这就发生在step2。
第二，在一个连续环境里，我们可以使用平均value，因为我们无法依赖一个具体的start state。
每个state的value通过对应state触发的概率进行加权。

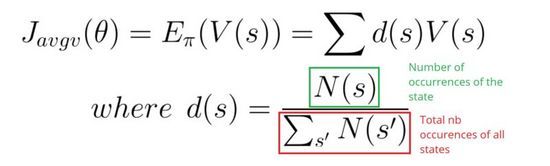
第三，我们可以使用每个时间步的平均reward。这里思想就是在每个时间步我们想要得到更多的reward。

Second step: Policy gradient ascent

我们使用策略分数函数来告知我们策略的好坏。现在，我们想要找到一组参数来最优化我们的分数函数。
最大化分数函数意味着寻找最优策略。
为了最大化分数函数$J(\theta )$，我们需要在policy参数上做梯度上升。
梯度上升与梯度下降相反。记住梯度总是指向变化最明显的点。
为什么我们使用梯度上升而不是梯度下降呢？因为我们我们的分数函数并不是error函数，我们要求的是最大值不是最小值。
思想就是找到当前policy的梯度，然后根据梯度方向更新参数，然后迭代。

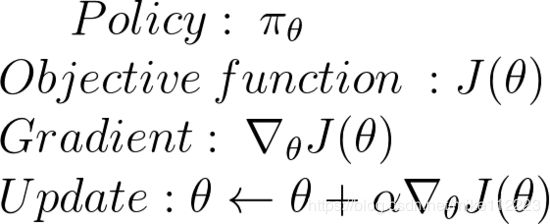
好了，现在我们来数学上实现这个。
我们想要找到最优参数：

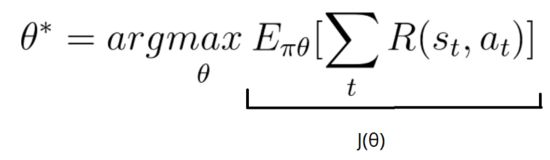
我们的分数函数被定义为：

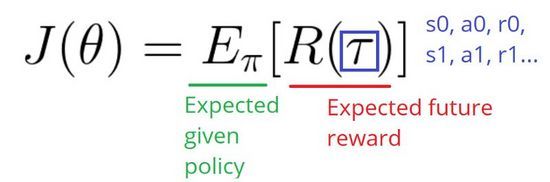
这是在给定policy下，期望reward的总和。
现在，因为我们想要做梯度上升，我们需要对分数函数求导。我们的分数函数也可以被定义为：

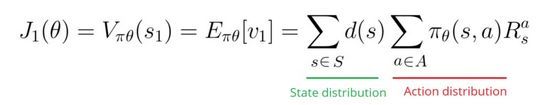
我们这样写是为了展示我们所面临的问题。
我们知道policy的参数会改变actions的选择，这会影响到我们得到的rewards，会看见的states以及看见这些states的频率。
所以，要找到policy改变来确保提升是很具有挑战性的。这是因为性能取决于动作的选择和做这些选择的states的分布。policy的参数同时影响这上述两点。policy参数对于动作的影响是很容易找到的，但是我们如何找到对于state分布的影响呢？环境函数是未知的。
因此，我们面临一个问题：如何估计基于policy 参数$\theta$的$\nabla$（gradient）？它之所以是个问题是因为梯度取决于策略改变带来的对于state的分布的未知影响。
解决方法将会用到Policy Gradient Theorem。该理论为我们提供了一个关于分数函数$J(\theta )$的梯度的解析表达式，且并不引入对于state分布的微分。
计算如下：


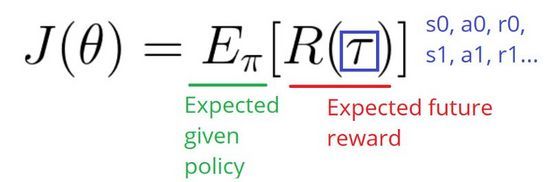
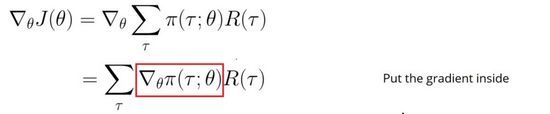
记住，我们实在使用随机策略。这意味着我们的策略输出的是一个概率分布$\pi (\tau ;\theta )$。它输出的是在当前参数下，采取一系列步骤（$s_0,a_0,r_0,......$）的可能性。
但是对于一个概率函数进行求导是很难的，除非可以转化成对数形式。这会简单很多。
这里我们用到一个似然比trick来将分式替换成对数概率。

现在我们将求和转换成期望：

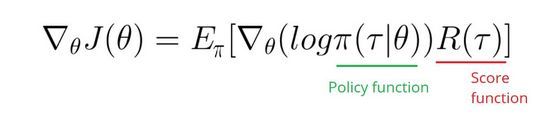
正如你看到的，我只需要计算对数policy函数的偏导就可以了。
好了说了这么多，现在我们来对policy gradients进行总结：

这个Policy gradient方法告诉我们如果我们想要取得更高的分数，我们需要通过改变policy参数来改变policy的分布。
$R(\tau )$像是一个价值分数标量：

• 如果$R(\tau )$高，说明平均看来，我们采取的动作会得到高回报。我们想要推动我们的概率分布倾向于见过的动作（增加采取这些动作的概率）。
• 相反，如果$R(\tau )$很低，我们想要减小见过动作的概率。

Policy Gradient会推动参数往拥有高回报的期望actions的方向走。

Monte Carlo Policy Gradients

对于情景采样任务，我们使用蒙特卡洛方法来设计policy gradient算法。

Initialize θ
for each episode τ = S0, A0, R1, S1, …, ST:
    for t <-- 1 to T-1:
		Δθ = α ∇theta(log π(St, At, θ)) Gt
		θ = θ + Δθ

For each episode:
    At each time step within that episode:
             Compute the log probabilities produced by our policy function. Multiply it by the score function.         
             Update the weights

但是对于这个算法我们面临一个问题。因为我仅计算情景结束时的rewards，我们平均了所有actions。即使一些actions的效果很差，如果我们的score很高，平均下来所有actions的结果都不错。
为了纠正这个policy，我们需要大量的样本，这就导致缓慢学习。

How to improve our Model？

下一篇我们会提到一些提升方法：

• Actor Critic：value-based算法和policy-based算法的混合。
• Proximal Policy Gradients：确保先前policy的偏导很小。