使用ID3算法构建决策树

原文地址：http://www.cise.ufl.edu/~ddd/cap6635/Fall-97/Short-papers/2.htm，
翻译水平有限，建议直接阅读原文

特征选取

在构造决策树时，我们需要解决的第一个问题就是，当前数据集上那个特征在划分时起决定作用。为了找到决定性特征，划分出最好结果，我们必须评估每个特征。在这里使用信息增益，增益可以描述用一个指定特征去划分数据集的好坏。选择增益最大的那个作为划分依据。为了定义增益，首先引入熵（Entropy）的概念。

给定数据集S，它的输出是c（c可以有多个类别）

Entropy(S) = S -p(I) log2 p(I)

I是c的一个类别，p(I)是类别I在集合S中的比例。

S是整个数据集。

Example 1

如果 S 有 14 个成员，9个YES，5个NO：

Entropy(S) = - (9/14) Log2 (9/14) - (5/14) Log2 (5/14) = 0.940

如果Entropy=0表示所有S的成员都属于同一类（可以考虑log2函数的图像过（1，0）点）。

我们定义特征A在在数据集S上的信息增益Gain(S, A):

Gain(S,A)=Entropy(S)-S((|S_v|/|S|)*Entropy(S_v))

S -表示特征A上所有可能的v值

_{Sv-数据集S中特征A的值为v的数据子集}

_{|Sv|-Sv的数量}

_{|S|-S的数量}

Example 2

假设 S 是一个有14个成员的数据集，它的一个属性是 wind speed。Wind可以有 Weak 和 Strong。这14个成员的分类结果是9个YES,5个NO。

对于特征 Wind，假设出现8次 Wind=Weak、6次 Wind=Strong，

对于 Wind=Weak, 6个YES、2个NO；对于 Wind = Strong, 3个YES、3个NO。因此：

Gain(S,Wind)=Entropy(S)-(8/14)*Entropy(S_weak)-(6/14)*Entropy(S_strong)

= 0.940 - (8/14)*0.811 - (6/14)*1.00

= 0.048

Entropy(S_weak) = - (6/8)*log2(6/8) - (2/8)*log2(2/8) = 0.811

Entropy(S_strong) = - (3/6)*log2(3/6) - (3/6)*log2(3/6) = 1.00

Example of ID3

假设我们想通过ID3决定是否天气适合去打棒球.我们统计了2周的数据去帮助ID3算法创建决策树（Table 1）。

我们分类目的是通过当前的天气决定去打棒球，结果是 yes 或者 no。

天气的属性有 outlook, temperature, humidity, and wind speed.他们可能的结果如下：

outlook = { sunny, overcast, rain }

temperature = {hot, mild, cool }

humidity = { high, normal }

wind = {weak, strong }

下面是S的数据集：

Day	Outlook	Temperature	Humidity	Wind	Play ball
D1	Sunny	Hot	High	Weak	No
D2	Sunny	Hot	High	Strong	No
D3	Overcast	Hot	High	Weak	Yes
D4	Rain	Mild	High	Weak	Yes
D5	Rain	Cool	Normal	Weak	Yes
D6	Rain	Cool	Normal	Strong	No
D7	Overcast	Cool	Normal	Strong	Yes
D8	Sunny	Mild	High	Weak	No
D9	Sunny	Cool	Normal	Weak	Yes
D10	Rain	Mild	Normal	Weak	Yes
D11	Sunny	Mild	Normal	Strong	Yes
D12	Overcast	Mild	High	Strong	Yes
D13	Overcast	Hot	Normal	Weak	Yes
D14	Rain	Mild	High	Strong	No

Table 1

我们需要计算这4个属性的增益，决定那个属性是决策树的根节点。

Gain(S, Outlook) = 0.246

Gain(S, Temperature) = 0.029

Gain(S, Humidity) = 0.151

Gain(S, Wind) = 0.048 (calculated in example 2)

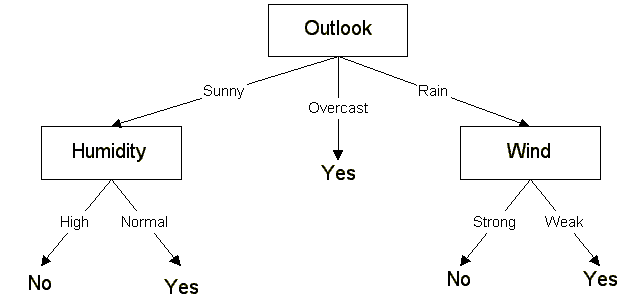
Outlook属性有最高的增益，因此它被作为决策的根节点。

因为Outlook有3个可能的值，根节点有3个分支(sunny, overcast, rain)。接着我们需要在Sunny节点测试剩余的3个属性:Humidity, Temperature, Wind.

S_sunny = {D1, D2, D8, D9, D11} , outlook = sunny

Gain(S_sunny, Humidity) = 0.970

Gain(S_sunny, Temperature) = 0.570

Gain(S_sunny, Wind) = 0.019

Humidity有最高的增益，因此作为一个节点。重复以上过程直道分类完成或者我们测试完所有属性。