传智播客 朴素贝叶斯 算法评估 交叉验证与网格搜索 学习
目录
朴素贝叶斯
概率论基础
sklearn.naive_bayes.MultinomialNB
互联网新闻分类
朴素贝叶斯-贝叶斯公式
拉普拉斯平滑
朴素贝叶斯分类优缺点
交叉验证
模型检验-交叉验证
训练集与测试集
holdout method
k-折交叉验证
交叉验证过程
超参数搜索-网格搜索
超参数搜索-网格搜索API
estimator的工作流程
分类器性能评估
sklearn.metrics.classification_report
朴素贝叶斯
朴素贝叶斯(Naive Bayes)是一个非常简单,但是实用性很强的分类模型。朴素贝叶斯分类器的构造基础是贝叶斯理论。
概率论基础
概率定义为一件事情发生的可能性。事情发生的概率可以 通过观测数据中的事件发生次数来计算,事件发生的概率等于改事件发生次数除以所有事件发生的总次数。举一些例子:
- 扔出一个硬币,结果头像朝上
- 某天是晴天
- 某个单词在未知文档中出现
我们将事件的概率记作P\left({X}\right)P(X),那么假设这一事件为X属于样本空间中的一个类别,那么{0}\le{P}\left({X}\right)\le{1}0≤P(X)≤1。
联合概率与条件概率
- 联合概率
是指两件事情同时发生的概率。那么我们假设样本空间有一些天气数据:
| 编号 | 星期几 | 天气 |
|---|---|---|
| 1 | 2 | 晴天 |
| 2 | 1 | 下雨 |
| 3 | 3 | 晴天 |
| 4 | 4 | 晴天 |
| 5 | 1 | 下雨 |
| 6 | 2 | 下雪 |
| 7 | 3 | 下雪 |
那么天气被分成了三类,那么P\left(X=sun\right){=}\frac{3}{7}P(X=sun)=73,假如说天气=下雪且星期几=2?这个概率怎么求?这个概率应该等于两件事情为真的次数除以所有事件发生 的总次数。我们可以看到只有一个样本满足天气=下雪且星期几=2,所以这个概率为\frac{1}{7}71。一般对于X和Y来说,对应的联合概率记为P\left({XY}\right)P(XY)。
- 条件概率
那么条件概率形如P\left({X}\mid{Y}\right)P(X∣Y),这种格式的。表示为在Y发生的条件下,发生X的概率。假设X代表星期,Y代表天气,则 P\left({X=3}\mid{Y=sun}\right)P(X=3∣Y=sun)如何求?
从表中我们可以得出,P\left({X=3,Y=sun}\right){=}\frac{1}{7}P(X=3,Y=sun)=71,P\left({Y}\right){=}\frac{3}{7}P(Y)=73
P\left({X=3}\mid{Y=sun}\right){=}\frac{1}{3}{=}\frac{P\left({X=3,Y=sun}\right)}{P\left({Y}\right)}P(X=3∣Y=sun)=31=P(Y)P(X=3,Y=sun)
在条件概率中,有一个重要的特性
- 如果每个事件之间相互独立
那么则有P\left({X_1,X_2,X_3,...,X_n}\mid{Y_i}\right){=}{P}\left({X_1}\mid{Y_i}\right) {P}\left({X_2}\mid{Y_i}\right) {P}\left({X_3}\mid{Y_i}\right){...}{P}\left({X_n}\mid{Y_i}\right)P(X1,X2,X3,...,Xn∣Yi)=P(X1∣Yi)P(X2∣Yi)P(X3∣Yi)...P(Xn∣Yi)
这个式子的意思是给定条件下,所有的X的概率为单独的Y条件下每个X发生的概率乘积,我们通过后面再继续去理解这个式子的具体含义。
贝叶斯公式
首先我们给出该公式的表示,P\left({c_i}\mid{W}\right){=}\frac{P\left({W}\mid{C_i}\right)P\left({c_i}\right)}{P\left({W}\right)}P(ci∣W)=P(W)P(W∣Ci)P(ci),其中c_ici为类别,WW为特征向量。
贝叶斯公式最常用于文本分类,上式左边可以理解为给定一个文本词向量WW,那么它属于类别c_ici的概率是多少。那么式子右边分几部分,P\left({W}\mid{c_i}\right)P(W∣ci)理解为在给定类别的情况下,该文档的词向量的概率。可以通过条件概率中的重要特性来求解。
假设我们有已分类的文档,
a = "life is short,i like python"
b = "life is too long,i dislike python"
c = "yes,i like python"
label=[1,0,1]
词袋法的特征值计算
若使用词袋法,且以训练集中的文本为词汇表,即将训练集中的文本中出现的单词(不重复)都统计出来作为词典,那么记单词的数目为n,这代表了文本的n个维度。以上三个文本在这8个特征维度上的表示为:
| life | is | i | short | long | like | dislike | too | python | yes | |
|---|---|---|---|---|---|---|---|---|---|---|
| a' | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| b' | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| c' | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
上面a',b'就是两个文档的词向量的表现形式,对于贝叶斯公式,从label中我们可以得出两个类别的概率为:
P\left({c_i=1}\right){=}0.5,P\left({c_i=0}\right){=}0.5P(ci=1)=0.5,P(ci=0)=0.5
对于一个给定的文档类别,每个单词特征向量的概率是多少呢?
提供一种TF计算方法,为类别y_kyk每个单词出现的次数N_iNi,除以文档类别y_kyk中所有单词出现次数的总数NN:
P_i{=}\frac{N_i}{N}Pi=NNi
首先求出现总数,对于1类别文档,在a'中,就可得出总数为1+1+1+1+1+1=6,c'中,总共1+1+1+1=4,故在1类别文档中总共有10次
每个单词出现总数,假设是两个列表,a'+c'就能得出每个单词出现次数,比如P\left({w=python}\right){=}\frac{2}{10}{=}{0.20000000}P(w=python)=102=0.20000000,同样可以得到其它的单词概率。最终结果如下:
# 类别1文档中的词向量概率
p1 = [0.10000000,0.10000000,0.20000000,0.10000000,0,0.20000000,0,0,0.20000000,0.10000000]
# 类别0文档中的词向量概率
p0 = [0.16666667,0.16666667,0.16666667,0,0.16666667,0,0.16666667,0.16666667,0.16666667,0]
拉普拉斯平滑系数
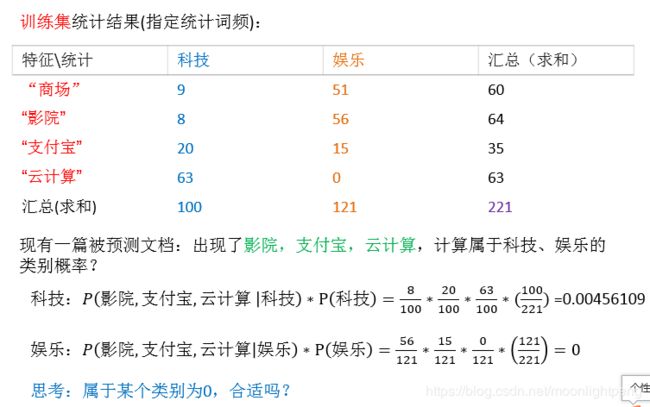
为了避免训练集样本对一些特征的缺失,即某一些特征出现的次数为0,在计算P\left({X_1,X_2,X_3,...,X_n}\mid{Y_i}\right)P(X1,X2,X3,...,Xn∣Yi)的时候,各个概率相乘最终结果为零,这样就会影响结果。我们需要对这个概率计算公式做一个平滑处理:
P_i{=}\frac{N_i+\alpha}{N+\alpha*m}Pi=N+α∗mNi+α
其中mm为特征词向量的个数,\alphaα为平滑系数,当\alpha{=}1α=1,称为拉普拉斯平滑
sklearn.naive_bayes.MultinomialNB
class sklearn.naive_bayes.MultinomialNB(alpha=1.0, fit_prior=True, class_prior=None)
"""
:param alpha:float,optional(default = 1.0)加法(拉普拉斯/ Lidstone)平滑参数(0为无平滑)
"""
互联网新闻分类
读取20类新闻文本的数据细节
from sklearn.datasets import fetch_20newsgroups
news = fetch_20newsgroups(subset='all')
print news.data[0]
上述代码得出该数据共有18846条新闻,但是这些文本数据既没有被设定特征,也没有数字化的亮度。因此,在交给朴素贝叶斯分类器学习之前,要对数据做进一步的处理。
20类新闻文本数据分割
from sklearn.cross_validation import train_test_split
X_train,X_test,y_train,y_test = train_test_split(news.data,news.target,test_size=0.25,random_state=42)
文本转换为特征向量进行TF特征抽取
from sklearn.feature_extraction.text import CountVectorizer
vec = CountVectorizer()
# 训练数据输入,并转换为特征向量
X_train = vec.fit_transform(X_train)
# 测试数据转换
X_test = vec.transform(X_test)
朴素贝叶斯分类器对文本数据进行类别预测
from sklearn.naive_bayes import MultinomialNB
# 使用平滑处理初始化的朴素贝叶斯模型
mnb = MultinomialNB(alpha=1.0)
# 利用训练数据对模型参数进行估计
mnb.fit(X_train,y_train)
# 对测试验本进行类别预测。结果存储在变量y_predict中
y_predict = mnb.predict(X_test)
性能测试
- 特点分析
朴素贝叶斯模型被广泛应用于海量互联网文本分类任务。由于其较强的特征条件独立假设,使得模型预测所需要估计的参数规模从幂指数量级想线性量级减少,极大的节约了内存消耗和计算时间。到那时,也正是受这种强假设的限制,模型训练时无法将各个特征之间的联系考量在内,使得该模型在其他数据特征关联性较强的分类任务上的性能表现不佳
朴素贝叶斯-贝叶斯公式
拉普拉斯平滑
sklearn朴素贝叶斯实现API
朴素贝叶斯分类优缺点
交叉验证
交叉验证:为了让被评估的模型更加准确可信
模型检验-交叉验证
一般在进行模型的测试时,我们会将数据分为训练集和测试集。在给定的样本空间中,拿出大部分样本作为训练集来训练模型,剩余的小部分样本使用刚建立的模型进行预测。
训练集与测试集
训练集与测试集的分割可以使用cross_validation中的train_test_split方法,大部分的交叉验证迭代器都内建一个划分数据前进行数据索引打散的选项,train_test_split 方法内部使用的就是交叉验证迭代器。默认不会进行打散,包括设置cv=some_integer(直接)k折叠交叉验证的cross_val_score会返回一个随机的划分。如果数据集具有时间性,千万不要打散数据再划分!
- sklearn.cross_validation.train_test_split
def train_test_split(*arrays,**options)
"""
:param arrays:允许的输入是列表,数字阵列
:param test_size:float,int或None(默认为无),如果浮点数应在0.0和1.0之间,并且表示要包括在测试拆分中的数据集的比例。如果int,表示测试样本的绝对数
:param train_size:float,int或None(默认为无),如果浮点数应在0.0到1.0之间,表示数据集包含在列车拆分中的比例。如果int,表示列车样本的绝对数
:param random_state:int或RandomState,用于随机抽样的伪随机数发生器状态,参数 random_state 默认设置为 None,这意为着每次打散都是不同的。
"""
from sklearn.cross_validation import train_test_split
from sklearn import datasets
iris = datasets.load_iris()
print iris.data.shape,iris.target.shape
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.4, random_state=42)
print X_train.shape,y_train.shape
print X_test.shape,y_test.shape
上面的方式也有局限。因为只进行一次测试,并不一定能代表模型的真实准确率。因为,模型的准确率和数据的切分有关系,在数据量不大的情况下,影响尤其突出。所以还需要一个比较好的解决方案。
模型评估中,除了训练数据和测试数据,还会涉及到验证数据。使用训练数据与测试数据进行了交叉验证,只有这样训练出的模型才具有更可靠的准确率,也才能期望模型在新的、未知的数据集上,能有更好的表现。这便是模型的推广能力,也即泛化能力的保证。
holdout method
评估模型泛化能力的典型方法是holdout交叉验证(holdout cross validation)。holdout方法很简单,我们只需要将原始数据集分割为训练集和测试集,前者用于训练模型,后者用于评估模型的性能。一般来说,Holdout 验证并非一种交叉验证,因为数据并没有交叉使用。 随机从最初的样本中选出部分,形成交叉验证数据,而剩余的就当做训练数据。 一般来说,少于原本样本三分之一的数据被选做验证数据。所以这种方法得到的结果其实并不具有说服性
k-折交叉验证
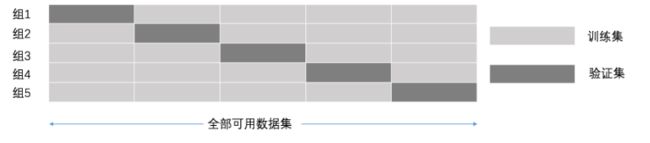
K折交叉验证,初始采样分割成K个子样本,一个单独的子样本被保留作为验证模型的数据,其他K-1个样本用来训练。交叉验证重复K次,每个子样本验证一次,平均K次的结果或者使用其它结合方式,最终得到一个单一估测。这个方法的优势在于,同时重复运用随机产生的子样本进行训练和验证,每次的结果验证一次,10折交叉验证是最常用的。
例如5折交叉验证,全部可用数据集分成五个集合,每次迭代都选其中的1个集合数据作为验证集,另外4个集合作为训练集,经过5组的迭代过程。交叉验证的好处在于,可以保证所有数据都有被训练和验证的机会,也尽最大可能让优化的模型性能表现的更加可信。
使用交叉验证的最简单的方法是在估计器和数据集上使用cross_val_score函数。
- sklearn.cross_validation.cross_val_score
def cross_val_score(estimator, X, y=None, groups=None, scoring=None, cv=None, n_jobs=1, verbose=0, fit_params=None, pre_dispatch='2*n_jobs')
"""
:param estimator:模型估计器
:param X:特征变量集合
:param y:目标变量
:param cv:int,使用默认的3折交叉验证,整数指定一个(分层)KFold中的折叠数
:return :预估系数
"""
from sklearn.cross_validation import cross_val_score
diabetes = datasets.load_diabetes()
X = diabetes.data[:150]
y = diabetes.target[:150]
lasso = linear_model.Lasso()
print(cross_val_score(lasso, X, y))
使用交叉验证方法的目的主要有2个:
- 从有限的学习数据中获取尽可能多的有效信息;
- 可以在一定程度上避免过拟合问题。
交叉验证过程
交叉验证:将拿到的数据,分为训练和验证集。以下图为例:将数据分
成5份,其中一份作为验证集。然后经过5次(组)的测试,每次都更换不同
的验证集。即得到5组模型的结果,取平均值作为最终结果。又称5折交叉
验证。
超参数搜索-网格搜索
通常情况下,有很多参数是需要手动指定的(如k-近邻算法中的K值),这种叫超参数。但是手动过程繁杂,所以需要对模型预设几种超参数组合。每组超参数都采用交叉验证来进行评估。最后选出最优参数组合建立模型。
| K值 |
K=3 |
K=5 |
K=7 |
| 模型 |
模型1 |
模型2 |
模型3 |
超参数搜索-网格搜索API
estimator的工作流程
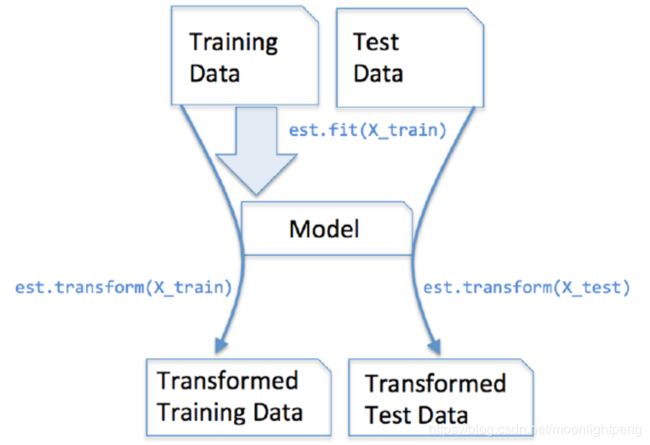
在sklearn中,估计器(estimator)是一个重要的角色,分类器和回归器都属于estimator。在估计器中有有两个重要的方法是fit和transform。
- fit方法用于从训练集中学习模型参数
- transform用学习到的参数转换数据
分类器性能评估
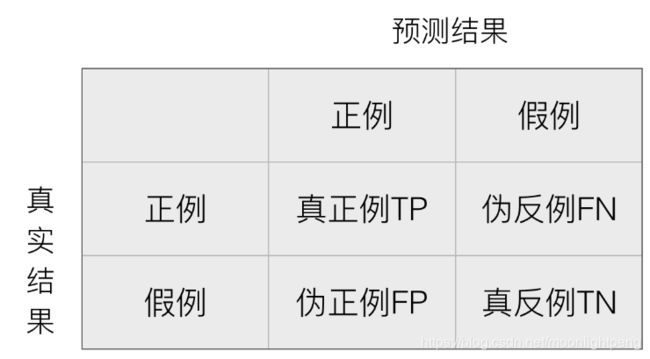
在许多实际问题中,衡量分类器任务的成功程度是通过固定的性能指标来获取。一般最常见使用的是准确率,即预测结果正确的百分比。然而有时候,我们关注的是负样本是否被正确诊断出来。例如,关于肿瘤的的判定,需要更加关心多少恶性肿瘤被正确的诊断出来。也就是说,在二类分类任务下,预测结果(Predicted Condition)与正确标记(True Condition)之间存在四种不同的组合,构成混淆矩阵。
在二类问题中,如果将一个正例判为正例,那么就可以认为产生了一个真正例(True Positive,TP);如果对一个反例正确的判为反例,则认为产生了一个真反例(True Negative,TN)。相应地,两外两种情况则分别称为伪反例(False Negative,FN,也称)和伪正例(False Positive,TP),四种情况如下图:
在分类中,当某个类别的重要性高于其他类别时,我们就可以利用上述定义出多个逼错误率更好的新指标。第一个指标就是正确率(Precision),它等于TP/(TP+FP),给出的是预测为正例的样本中占真实结果总数的比例。第二个指标是召回率(Recall)。它等于TP/(TP+FN),给出的是预测为正例的真实正例占所有真实正例的比例。
那么除了正确率和精确率这两个指标之外,为了综合考量召回率和精确率,我们计算这两个指标的调和平均数,得到F1指标(F1 measure):
{F1}={\frac{2}{\frac{1}{Precision}{+}\frac{1}{Recall}}}F1=Precision1+Recall12
之所以使用调和平均数,是因为它除了具备平均功能外,还会对那些召回率和精确率更加接近的模型给予更高的分数;而这也是我们所希望的,因为那些召回率和精确率差距过大的学习模型,往往没有足够的使用价值。
sklearn.metrics.classification_report
sklearn中metrics中提供了计算四个指标的模块,也就是classification_report。
classification_report(y_true, y_pred, labels=None, target_names=None, digits=2)
"""
计算分类指标
:param y_true:真实目标值
:param y_pred:分类器返回的估计值
:param target_names:可选的,计算与目标类别匹配的结果
:param digits:格式化输出浮点值的位数
:return :字符串,三个指标值
"""
我们通过一个例子来分析一下指标的结果:
from sklearn.metrics import classification_report
y_true = [0, 1, 2, 2, 2]
y_pred = [0, 0, 2, 2, 1]
target_names = ['class 0', 'class 1', 'class 2']
print(classification_report(y_true, y_pred, target_names=target_names))
precision recall f1-score support
class 0 0.50 1.00 0.67 1
class 1 0.00 0.00 0.00 1
class 2 1.00 0.67 0.80 3
avg / total 0.70 0.60 0.61 5from sklearn.datasets import load_iris, fetch_20newsgroups, load_boston
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import classification_report
from sklearn.feature_extraction import DictVectorizer
from sklearn.tree import DecisionTreeClassifier, export_graphviz
from sklearn.ensemble import RandomForestClassifier
import pandas as pd
# li = load_iris()
# print("获取特征值")
# print(li.data)
# print("目标值")
# print(li.target)
# print(li.DESCR)
# 注意返回值, 训练集 train x_train, y_train 测试集 test x_test, y_test
# x_train, x_test, y_train, y_test = train_test_split(li.data, li.target, test_size=0.25)
#
# print("训练集特征值和目标值:", x_train, y_train)
# print("测试集特征值和目标值:", x_test, y_test)
# news = fetch_20newsgroups(subset='all')
#
# print(news.data)
# print(news.target)
#
# lb = load_boston()
#
# print("获取特征值")
# print(lb.data)
# print("目标值")
# print(lb.target)
# print(lb.DESCR)
def knncls():
"""
K-近邻预测用户签到位置
:return:None
"""
# 读取数据
data = pd.read_csv("./data/FBlocation/train.csv")
# print(data.head(10))
# 处理数据
# 1、缩小数据,查询数据晒讯
data = data.query("x > 1.0 & x < 1.25 & y > 2.5 & y < 2.75")
# 处理时间的数据
time_value = pd.to_datetime(data['time'], unit='s')
print(time_value)
# 把日期格式转换成 字典格式
time_value = pd.DatetimeIndex(time_value)
# 构造一些特征
data['day'] = time_value.day
data['hour'] = time_value.hour
data['weekday'] = time_value.weekday
# 把时间戳特征删除
data = data.drop(['time'], axis=1)
print(data)
# 把签到数量少于n个目标位置删除
place_count = data.groupby('place_id').count()
tf = place_count[place_count.row_id > 3].reset_index()
data = data[data['place_id'].isin(tf.place_id)]
# 取出数据当中的特征值和目标值
y = data['place_id']
x = data.drop(['place_id'], axis=1)
# 进行数据的分割训练集合测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25)
# 特征工程(标准化)
std = StandardScaler()
# 对测试集和训练集的特征值进行标准化
x_train = std.fit_transform(x_train)
x_test = std.transform(x_test)
# 进行算法流程 # 超参数
knn = KNeighborsClassifier()
# # fit, predict,score
# knn.fit(x_train, y_train)
#
# # 得出预测结果
# y_predict = knn.predict(x_test)
#
# print("预测的目标签到位置为:", y_predict)
#
# # 得出准确率
# print("预测的准确率:", knn.score(x_test, y_test))
# 构造一些参数的值进行搜索
param = {"n_neighbors": [3, 5, 10]}
# 进行网格搜索
gc = GridSearchCV(knn, param_grid=param, cv=2)
gc.fit(x_train, y_train)
# 预测准确率
print("在测试集上准确率:", gc.score(x_test, y_test))
print("在交叉验证当中最好的结果:", gc.best_score_)
print("选择最好的模型是:", gc.best_estimator_)
print("每个超参数每次交叉验证的结果:", gc.cv_results_)
return None
def naviebayes():
"""
朴素贝叶斯进行文本分类
:return: None
"""
news = fetch_20newsgroups(subset='all')
# 进行数据分割
x_train, x_test, y_train, y_test = train_test_split(news.data, news.target, test_size=0.25)
# 对数据集进行特征抽取
tf = TfidfVectorizer()
# 以训练集当中的词的列表进行每篇文章重要性统计['a','b','c','d']
x_train = tf.fit_transform(x_train)
print(tf.get_feature_names())
x_test = tf.transform(x_test)
# 进行朴素贝叶斯算法的预测
mlt = MultinomialNB(alpha=1.0)
print(x_train.toarray())
mlt.fit(x_train, y_train)
y_predict = mlt.predict(x_test)
print("预测的文章类别为:", y_predict)
# 得出准确率
print("准确率为:", mlt.score(x_test, y_test))
print("每个类别的精确率和召回率:", classification_report(y_test, y_predict, target_names=news.target_names))
return None
def decision():
"""
决策树对泰坦尼克号进行预测生死
:return: None
"""
# 获取数据
titan = pd.read_csv("http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt")
# 处理数据,找出特征值和目标值
x = titan[['pclass', 'age', 'sex']]
y = titan['survived']
print(x)
# 缺失值处理
x['age'].fillna(x['age'].mean(), inplace=True)
# 分割数据集到训练集合测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25)
# 进行处理(特征工程)特征-》类别-》one_hot编码
dict = DictVectorizer(sparse=False)
x_train = dict.fit_transform(x_train.to_dict(orient="records"))
print(dict.get_feature_names())
x_test = dict.transform(x_test.to_dict(orient="records"))
# print(x_train)
# 用决策树进行预测
# dec = DecisionTreeClassifier()
#
# dec.fit(x_train, y_train)
#
# # 预测准确率
# print("预测的准确率:", dec.score(x_test, y_test))
#
# # 导出决策树的结构
# export_graphviz(dec, out_file="./tree.dot", feature_names=['年龄', 'pclass=1st', 'pclass=2nd', 'pclass=3rd', '女性', '男性'])
# 随机森林进行预测 (超参数调优)
rf = RandomForestClassifier(n_jobs=-1)
param = {"n_estimators": [120, 200, 300, 500, 800, 1200], "max_depth": [5, 8, 15, 25, 30]}
# 网格搜索与交叉验证
gc = GridSearchCV(rf, param_grid=param, cv=2)
gc.fit(x_train, y_train)
print("准确率:", gc.score(x_test, y_test))
print("查看选择的参数模型:", gc.best_params_)
return None
if __name__ == "__main__":
decision()